DIAGRAMS OF INTERNAL EFFORTS

Lecture



In cases of tension-compression (a) or torsion (b) the ordinates of the plot of the longitudinal forces or torques also show their values ​​in the corresponding cross-sections (Fig.1.11a.b).
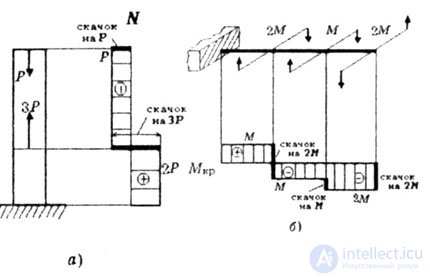DIAGRAMS OF INTERNAL EFFORTS
Fig. 1.11
Any internal force is determined by external loads using the section method.
Each plot on their sites has signs.
The rules of signs for internal efforts applied in mechanical engineering.
  1. The longitudinal force N is considered positive if it causes stretching of the cut-off part and negative if it causes compression.
  2. The shear force O is considered positive if it rotates the cut part in a clockwise direction and negative if the rotation occurs counterclockwise.
  3. The plot of bending moments is built on compressed fibers. The bending moment is positive if the upper fibers of the cut-off part are compressed, and negative if the lower fibers are compressed
  4. The rule of signs for torque is arbitrary.
It is usually agreed that when looking at the normal to the cut-off part, the internal torque is considered positive if it turns the cut-off part clockwise.
When bending between the transverse force Q, the bending moment M, the angle of rotation of the cross section 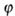DIAGRAMS OF INTERNAL EFFORTS and deflection Y there are differential dependences, allowing to establish the following characteristic features of plots:

1. Write the expression of bending moments for the current section z, for example, in a cantilever beam under the action of a concentrated force (Fig. 1.12):
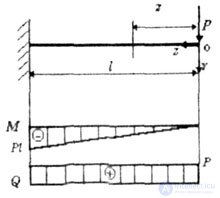DIAGRAMS OF INTERNAL EFFORTS
Fig. 1.12
M = - P * z - equation of a line.
In accordance with the differential dependence of Zhuravsky:
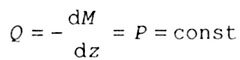DIAGRAMS OF INTERNAL EFFORTS
From this it follows that on a straight line, not loaded by an external flight load, the section of the rod of moments M is rectilinear, and the diagram of shear forces Q is constant (Figure 1.12).

2. At the point of application of a concentrated bending moment, the plot of moments of M has a jump by the magnitude of this moment, and the diagram of shear forces O is constant. At the point of application of concentrated torque, the plot of torque moments of M cr has a jump to this moment of fig. 1.11, b).

3. At the point of application of the concentrated transverse force, the curve of the bending moments has a jog with a tip toward the force, and the diagram of the transverse force is a jump by the magnitude of this force.

At the point of application of a concentrated longitudinal force, the diagram of the longitudinal forces A / also has a jump by the magnitude of this force.

4. Write the expression of bending moments for the current section z in the case of bending of a cantilever beam under the action of a distributed load (ois. 13.13 a):
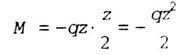DIAGRAMS OF INTERNAL EFFORTS
square parabola equation.
In accordance with the differential dependence of Zhuravsky:
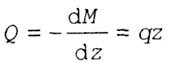DIAGRAMS OF INTERNAL EFFORTS
straight line equation.
Thus, in the section with a distributed load, the diagrams of the bending moments M are outlined along a square parabola with a bulge in opposition to the action of the distributed load, and the diagram of transverse forces Q has the form of a trapezoid or treugopnik. It is outlined with a straight, oblique line AB, with the direction of inclination (when going from left to right) coinciding with direction q (Fig. 1.13 a, b, c).
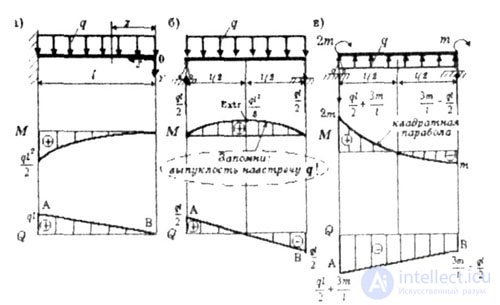DIAGRAMS OF INTERNAL EFFORTS
Fig. 1.13

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Strength of materials

Terms: Strength of materials