Lecture
| For pivotally fixed, centrally compressed rod of constant cross section (Fig. 8.2). I Euler's formula is: |
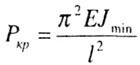 |
| where E is the modulus of the longitudinal elasticity of the material of the rod; |
| J min - the minimum moment of inertia of the cross section of the rod. |
| For rods with other types of binding, Euler's formula is written in the form: |
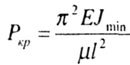 |
Where 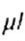 - given the length of the rod; - given the length of the rod; |
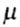 - coefficient of bringing the length. - coefficient of bringing the length. |
The expression "reduced length" means that in the Euler formula using the coefficient 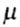 all cases of fastening of the ends of the rod can be brought to the main, hinged fastening. all cases of fastening of the ends of the rod can be brought to the main, hinged fastening. |
Length reduction factor 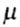 sometimes it can be estimated by the number of half-waves n for which the rod will bulge, losing stability, namely, we can take sometimes it can be estimated by the number of half-waves n for which the rod will bulge, losing stability, namely, we can take |
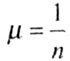 |
In fig. 8.2 shows the cases of fixing the ends of the rod that are most frequently encountered in practice and the corresponding values of the coefficient 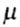 |
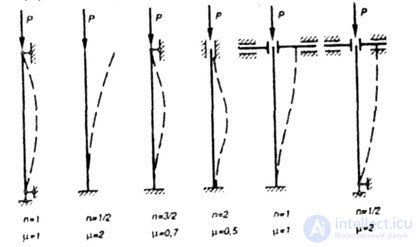 |
| Fig. 8.2 |
Euler's formula is applicable only on the limits of Hooke’s law, when the critical stress 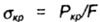 does not exceed the limit of proportionality of the material of the rod, since this formula was introduced using the dependence does not exceed the limit of proportionality of the material of the rod, since this formula was introduced using the dependence |
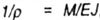 |
| in due time received on the basis of Hooke's law. |
| The applicability of the Euler formula can be determined by evaluating the flexibility of the rod and comparing this flexibility with its limit value. Rod flexibility is equal to |
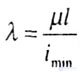 |
| Where |
 - minimum radius of inertia (geometric characteristic of the section); - minimum radius of inertia (geometric characteristic of the section); |
 - the minimum moment of inertia of the cross-sectional area of the rod. - the minimum moment of inertia of the cross-sectional area of the rod. |
Marginal flexibility value 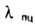 is obtained from the condition is obtained from the condition |
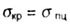 |
| Ultimate flexibility equal to |
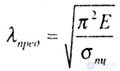 |
| So, for mild steel, if we take E = 2x10 5 MPa, |
 |
To increase the bearing capacity of structures, they strive to use rods of as little flexibility as possible. So the calculation of real structures with flexibility 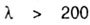 practically unlikely. We assume practically unlikely. We assume 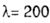 |
| the upper boundary of the values of the flexibility of real rods. |
| Consequently, the Euler formula for determining the critical value of the compressive force in the form |
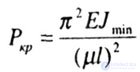 |
| applicable in case the rod flexibility is within |
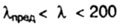 |
| (LED curve in Fig. 8.3) |
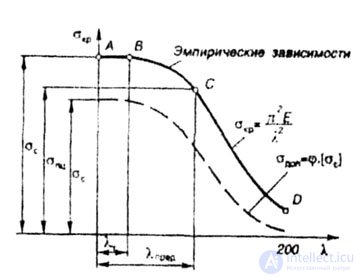 |
| Fig. 8.3 |
| For mild steel this range is equal to |
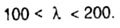 |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials