You get a bonus - 1 coin for daily activity. Now you have 1 coin

BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH

Lecture



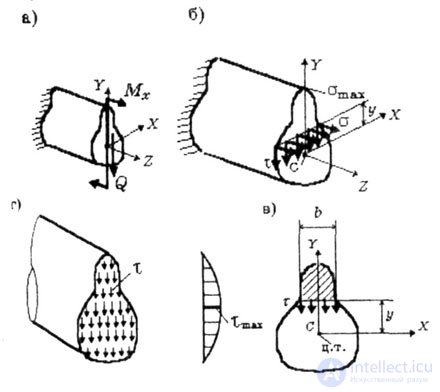
At all points of the timber cross section, normal and tangential stresses occur during lateral bending (in Fig. 5.1.6, these stresses are shown at points at a distance of Y from the X axis):
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
Fig. 5.1
Legend.
M x , Q - internal forces: bending moment and shear force, they vary along the beam and are determined by plotting;
y is the coordinate of the cross-section points at which stresses are determined;
b is the width of the cross section at the point where shear stresses are determined;
J x - the main central moment of inertia is the moment of inertia about the central axis x,
с x * is the static moment relative to the neutral axis z of that part of the cross-sectional area, which is located above (or below) the longitudinal section — above or below the level y, at the points of which the tangential stresses are determined.
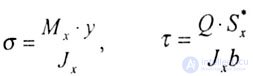BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
These formulas are derived in the main central axes of the beam cross section. In fig. 5.1 is the X, Y axes. The Y axis coincides with the axis of symmetry of the section, and the X axis, perpendicular to the bend plane, passes through the center of gravity of the section and is the neutral axis: the normal stresses at the points of this axis are zero. Z axis - the axis of the beam.
Thus, at the level of voltage, defined by the above formulas, are constant, do not depend on the coordinate X.
With an increase in the coordinate y, the normal stresses increase and at the points farthest from the neutral axis reach the highest value:
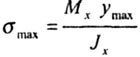BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
For calculations, a special geometrical characteristic is used - the moment of section resistance during bending:
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
The tangential stresses, on the contrary, decrease and in the most distant from the neutral axis the points vanish, and the regions of the neutral axis reach the highest values ​​(Fig. 5.1, d). In addition, the highest values ​​of tangential stresses are significantly less than the maximum values ​​of normal stresses: so for a cantilever rod of rectangular cross section loaded with a concentrated force at the free end, the ratio of the maximum values ​​of these stresses
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
where l, h is the length of the timber and the height of its cross section.
Therefore, when l >> h, which takes place in most cases, shear stresses are negligible compared to normal ones and are not taken into account in strength calculations.
The strength condition is as follows:
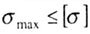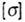BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH - allowable stress.
The process of calculating the beam strength should be conducted in a certain sequence. It is necessary:
  1. To determine the whole complex of external forces, including reactions of the supports.
    First of all, it is necessary to determine all reactions of the supports, since the reactions are among the external forces. If the number of reactions is equal to the number of linearly independent equations of statics, then all reactions are found from static equations.
  2. Construct plots of internal efforts, which determine the dangerous section.
    Plotting internal efforts is performed using the method of sections and begins with dividing the beam into sections. The boundaries of the plots are places of application of concentrated forces or moments, places of the beginning and end of the action of distributed loads.
Then, at each site, an arbitrary section is selected, for which expressions are drawn up to determine the internal efforts, which are used to plot the graphs of these efforts.
The diagrams of the internal forces determine the dangerous sections in which these efforts reach the highest values.
In most cases, the main internal force in the calculation of the beam strength is the bending moment and the associated normal stresses.

3. In hazardous sections, determine the maximum normal stresses and, for the greatest of these stresses, verify that the strength condition is met.
After determining the position of the dangerous sections with the largest values ​​of bending moments, in these sections the highest normal stresses are calculated:

a) For bars made of plastic material, with equal magnitude of yield strength in tension and compression, the highest design stresses occur in the "dangerous" points that are the most distant from the neutral axis.
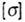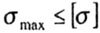These stresses are compared with the allowable voltage. BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH :
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
after which a conclusion is made about the strength of the timber.

b) If the beam is made of brittle material: then in dangerous sections the greatest normal stresses are determined both in stretched and compressed BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH cross-sectional zones and by comparing them with the appropriate allowable tensile stresses BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH and compression BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH :
BENDING TENSION AND CALCULATION OF BARS FOR STRENGTH
the question of the strength of the timber.
created: 2014-09-20
updated: 2024-11-09
286

Rating 9 of 10. count vote: 2
Are you satisfied?:

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Strength of materials

Terms: Strength of materials