Lecture
When calculating integrals, their diagrams are used instead of analytical expressions of moments. Those. value 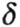 can be found by the Vereshchagin method, “multiplying” the diagrams of M p and M 1 .
can be found by the Vereshchagin method, “multiplying” the diagrams of M p and M 1 .
"Multiply" two epures - means the area of the nonlinear diagram of bending moments multiplied by the ordinate of another necessarily linear diagram that is under the center of gravity of the first, and the result divided by rigidity (in cases where both epures are linear, it is completely indifferent on which of them take the area, and on what the ordinate).
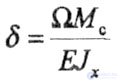
Where  - the area of an arbitrary shape;
- the area of an arbitrary shape;
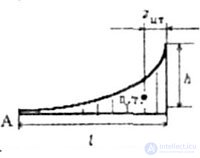
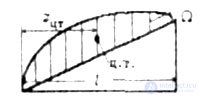
M c - the ordinate of the rectilinear plot, corresponding to the center of gravity of the area 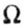 (Fig. 6.2).
(Fig. 6.2).
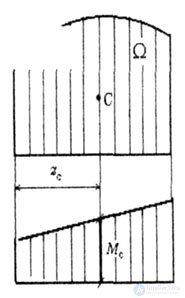
Fig. 6.2
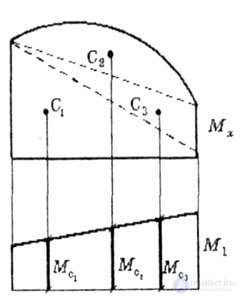
Fig. 6.3
Composition 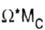 within the considered area is positive if the area
within the considered area is positive if the area  and the corresponding ordinate M c is located on the same side of the axis of this area, and negatively, if they are located on opposite sides.
and the corresponding ordinate M c is located on the same side of the axis of this area, and negatively, if they are located on opposite sides.
In cases where the plot is complex, to determine its area or coordinates of the center of gravity, the plot is broken down into simplest figures (Fig. 6.3), for which it is easy to determine the area and position of the center of gravity.
Thus, when defining movements using the Vereshchagin rule, the following sequence is followed:
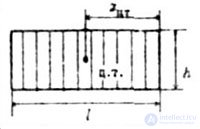
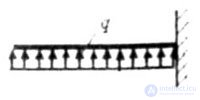
Below are the values of the areas of the figures and the coordinates of the centers of gravity of the simplest diagrams (Table 1).
Table 1.
|
Loading |
Bending moment plot view |
Center of gravity |
Size area |
|
|
|
|
|
 |
 |
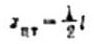 |
 |
 |
 |
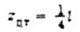 |
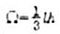 |
 |
 |
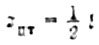 |
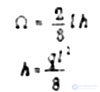 и и |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials