Lecture
Resistance of materials (in use - sopromat) is part of the mechanics of a deformable rigid body, which examines the methods of engineering calculations of structures for strength, rigidity and stability while meeting the requirements of reliability, efficiency and durability.
Resistance of materials is based on the concept of "strength", which is the ability of a material to withstand the applied loads and impacts without destruction. Resistance of materials operates with such concepts as: internal forces, stresses, deformations. The applied external load to a certain body generates internal efforts in it, counteracting the active action of the external load. Internal forces distributed over body sections are called stresses. Thus, the external load generates an internal reaction of the material, characterized by stresses, which in turn are directly proportional to the deformations of the body. Deformations are linear (elongation, shortening, shear) and angular (rotation of sections). The basic concepts of the resistance of materials, assessing the ability of a material to resist external influences:
In the theoretical part, the resistance of materials is based on mathematics and theoretical mechanics, in the experimental part - on physics and materials science and is used in the design of machines, instruments and structures. Practically all special disciplines of training engineers in various specialties contain sections of the course of resistance of materials, since the creation of a workable new equipment is impossible without analyzing and calculating its strength, rigidity and reliability.
The task of resistance of materials, as one of the sections of continuum mechanics, is to determine the strain and stress in a rigid elastic body, which is subjected to a force or heat effect.
This same task is considered among others in the course of the theory of elasticity. However, the methods for solving this common task in both the courses are significantly different from each other. Resistance of materials solves it mainly for timber, based on a number of hypotheses of a geometric or physical nature. Such a method makes it possible to obtain, although not in all cases, quite accurate, but rather simple formulas for calculating stresses. The theory of plasticity and the theory of viscoelasticity are also involved in the behavior of deformable solids under load.
The calculation of real structures and their elements is either theoretically impossible or practically unacceptable in its complexity. Therefore, in the resistance of materials, a model of an idealized deformable body is used, including the following assumptions and simplifications:
These provisions are limited to the specific tasks. For example, for solving the problems of stability, statements 4–6 are not valid, statement 3 is not always true.
Structural strength is determined using the theory of destruction - the science of predicting the conditions under which solid materials are destroyed by external loads. Materials, as a rule, are divided into crumbling and brittle. Depending on conditions (temperature, stress distribution, type of load, etc.), most materials can be classified as fragile, ductile, or both at the same time. However, for most practical situations, materials can be classified as fragile or ductile. Despite the fact that the theory of destruction has been under development for over 200 years, its level of acceptability for continuum mechanics is not always sufficient.
Mathematically, the theory of destruction is expressed in the form of various criteria of destruction, valid for specific materials. The criterion of destruction is the surface of destruction, expressed through stresses or deformations. The surface of destruction separates the “damaged” and “not damaged” states. For a “damaged” state, it is difficult to give an exact physical definition; this concept should be considered as a working definition used in the engineering community. The term "surface of destruction", used in the theory of strength, should not be confused with a similar term that defines the physical boundary between damaged and intact parts of the body. Quite often, the phenomenological criteria for the destruction of the same species are used to predict brittle and ductile failure.
Among the phenomenological theories of strength, the most famous are the following theories, which are commonly called "classical" theories of strength:
Classical strength theories have significant limitations for their application. So the theory of the greatest normal stresses and the greatest deformations are applicable only to calculate the strength of brittle materials, and only for some specific loading conditions. Therefore, these theories of strength today apply very limited. Of these theories, the most commonly used theory is Mohr, which is also called the Mohr-Coulomb criterion. Coulomb in 1781, on the basis of his tests, established the law of dry friction, which he used to calculate the stability of retaining walls. The mathematical formulation of the Coulomb's law coincides with the theory of Mohr, if it expresses the main stresses in terms of the tangential and normal stresses on the section of the slice. The advantage of Mohr's theory is that it is applicable to materials having different resistances to compression and tension, and the disadvantage is that it takes into account the influence of only two main stresses - maximum and minimum. Therefore, Mohr's theory does not accurately estimate the strength under a triaxial stress state, when it is necessary to take into account all three principal stresses. In addition, when using this theory, the lateral expansion (dilation) of the material during shear is not taken into account. A. A. Gvozdev, who repeatedly proved the inapplicability of Mohr's theory to concrete, repeatedly drew attention to these shortcomings of the Mora's theory. [one]
Replaced the "classical" theories of strength in modern practice came numerous new theories of destruction. Most of them use various combinations of Cauchy stress tensor invariants (Cauchy) Among them, the most well known are the following destruction criteria:
The listed strength criteria are designed to calculate the strength of homogeneous (homogeneous) materials. Some of them are used to calculate anisotropic materials.
To calculate the strength of inhomogeneous (non-homogeneous) materials, two approaches are used, called macro-modeling and micro-modeling. Both approaches are focused on the use of the finite element method and computer technology. In macro-modeling, homogenization is preliminarily performed — the conditional replacement of a heterogeneous (heterogeneous) material with a homogeneous (homogeneous) material. In micro-modeling, material components are considered taking into account their physical characteristics. Micro-modeling is mainly used for research purposes, since the calculation of real structures requires an excessively large expenditure of machine time. Methods of homogenization are widely used to calculate the strength of stone structures, primarily for the calculation of wall-diaphragm stiffness of buildings. Criteria for the destruction of stone structures take into account the diverse forms of destruction of masonry. Therefore, the surface of destruction, as a rule. taken in the form of several intersecting surfaces, which may have a different geometric shape.
Methods of resistance to materials are widely used in the calculation of load-bearing structures of buildings and structures in the disciplines related to the design of machine parts.
As a rule, it is because of the estimated nature of the results obtained using the mathematical models of this discipline when designing real structures all the strength characteristics of materials and products are selected with a substantial margin (several times relative to the result obtained in the calculations).
In the student environment, the resistance of materials is considered one of the most difficult general professional disciplines, mainly due to the severe dry theory theory, the lack of good visual teaching aids, computer modeling and training videos, which provided rich food for student folklore and gave rise to a number of jokes and anecdotes.
| Р - concentrated force (conditionally applied as if at one point) |
| g - intensity of the distributed load, force per unit length (N / m, MN / m) |
| M - external moment acting on the structural element (bending or twisting) |
| y - the proportion of material |
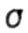 - normal stress (sigma - normal stress (sigma 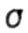 ) ) |
| t - shear stress (tau t) |
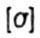 - allowable normal stress - allowable normal stress |
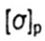 - allowable normal tensile stress - allowable normal tensile stress |
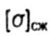 - permissible normal compressive stress - permissible normal compressive stress |
[t] - permissible shear stress [t] = (0.5 ... 0.6) [ 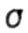 ] ] |
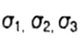 - principal stresses (extreme normal) - principal stresses (extreme normal) |
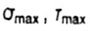 - maximum voltage - maximum voltage |
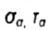 - stresses at an arbitrary inclined platform - stresses at an arbitrary inclined platform |
| n, n y - factors of safety and stability |
| N - longitudinal force |
| Q x , Q y - lateral forces |
| M x , M y - bending moments relative to the axes X and Y |
| M p - torque (relative to the longitudinal axis Z) |
| E - Young's modulus of elasticity for a wide range of materials (E = 2-10 5 MPa) |
| G is the shear modulus (G = 8 • 10 4 MPa) or G is the gradient of local stresses |
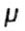 - Poisson's ratio - Poisson's ratio 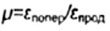 |
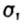 - yield strength - yield strength |
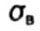 - tensile strength - tensile strength |
 - limit of proportionality - limit of proportionality |
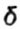 - relative longitudinal elongation (in the text, simply linear displacement from a single force) - relative longitudinal elongation (in the text, simply linear displacement from a single force) |
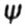 - relative transverse contraction - relative transverse contraction |
| u is the potential deformation energy |
| A - work of an external force |
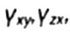 - angular shear deformations in different planes - angular shear deformations in different planes |
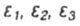 - main relative deformations - main relative deformations |
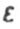 - relative longitudinal elongation (or shortening) - relative longitudinal elongation (or shortening) |
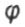 - the twisting angle of the cross section of the shaft during torsion or the reduction factor of the main to the voltage - the twisting angle of the cross section of the shaft during torsion or the reduction factor of the main to the voltage |
| d - diameter of a round rod |
| y - deflection of beams when bending |
| Z is the coordinate of an arbitrary section point when dissected using the ROSE method |
| F - cross-sectional area of rods, beams and shafts |
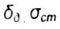 - generalized dynamic and ast static movements - generalized dynamic and ast static movements |
| G B - cargo weight |
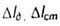 - change the length of the rod with a dynamic and static force - change the length of the rod with a dynamic and static force |
| U - potential energy |
| T - kinetic energy |
| dm is the particle mass of the elastic system |
| v - speed |
| T - temperature of absolute fragility |
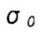 - endurance limit at a neutral (pulsating) cycle of standard samples - endurance limit at a neutral (pulsating) cycle of standard samples |
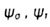 - coefficients characterizing the sensitivity of the material to cycle asymmetry - coefficients characterizing the sensitivity of the material to cycle asymmetry |
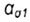 - theoretical stress concentration factor - theoretical stress concentration factor |
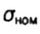 - the nominal voltage in did without a hub - the nominal voltage in did without a hub |
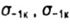 - limits the endurance of the sample with a stress concentration - limits the endurance of the sample with a stress concentration |
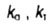 - effective stress concentration factors for bending and torsion - effective stress concentration factors for bending and torsion |
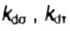 - factors taking into account the scale factor details - factors taking into account the scale factor details |
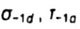 - endurance limit of smooth specimens with diameter d - endurance limit of smooth specimens with diameter d |
| G - gradient of local stresses |
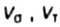 - sensitivity factors of metal to stress concentration and scale factor - sensitivity factors of metal to stress concentration and scale factor |
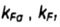 - coefficients that take into account the effect on the endurance limits of the part on the quality of surface treatment - coefficients that take into account the effect on the endurance limits of the part on the quality of surface treatment |
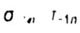 - limits the endurance of the sample with a given surface quality - limits the endurance of the sample with a given surface quality |
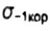 - endurance limit of the sample in a corrosive environment - endurance limit of the sample in a corrosive environment |
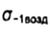 - endurance limit of the sample in air - endurance limit of the sample in air |
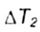 - shift of the critical temperature from the degree of stress concentration - shift of the critical temperature from the degree of stress concentration |
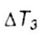 - critical temperature shift from increasing crack sizes - critical temperature shift from increasing crack sizes |
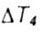 - shift of the critical temperature from repeated cyclic damage - shift of the critical temperature from repeated cyclic damage |
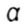 - stress concentration factor - stress concentration factor |
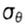 - circumferential stress in the vicinity of the crack - circumferential stress in the vicinity of the crack |
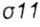 - the unit coefficient of the canonical equation of the method of forces - the unit coefficient of the canonical equation of the method of forces |
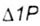 - cargo term of the canonical equation of the method of forces - cargo term of the canonical equation of the method of forces |
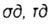 - normal and tangential dynamic stresses - normal and tangential dynamic stresses |
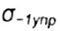 - endurance limit of the hardened sample - endurance limit of the hardened sample |
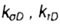 - coefficients of reducing the endurance limit of the part, respectively, in bending and torsion - coefficients of reducing the endurance limit of the part, respectively, in bending and torsion |
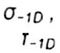 - endurance limits of the part - endurance limits of the part |
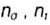 - safety factors, respectively, for normal tangential stresses - safety factors, respectively, for normal tangential stresses |
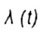 - failure rate - failure rate |
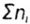 - the number of products that failed during time t - the number of products that failed during time t |
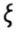 - function of indestructibility - function of indestructibility |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials