Lecture
| When determining the position of the center of gravity of the section, it is necessary to determine the values of the static moments of this section. |
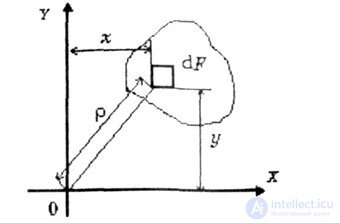 |
| Fig. 4.3 |
| The static moments of the cross section relative to the X and Y axes (Fig. 4.3) are defined integrals of the form: |
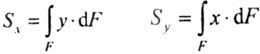 |
| where F is the section area; X and y - the coordinates of the element area dF. |
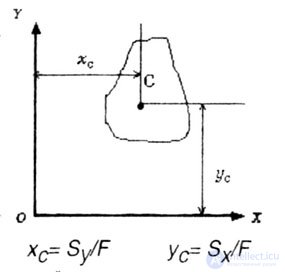
| If the position of the center of gravity of the section is known (Fig. 4.4). then the static moments of the section can be calculated by simple formulas, without taking integrals, namely |
 |
| where X c and Y c are the coordinates of the center of gravity of the section. |
| From expressions (2) you can determine the coordinates of the center of gravity of the section X c and Y c : |
 |
| The static moment of the section about the axis passing through the center of gravity is zero. |
| Axes passing through the center of gravity of the section are called central. The center of gravity of the section lies on the axis of symmetry of the section. If the cross section has at least two axes of symmetry, then the center of gravity lies at the intersection of these axes. |
| For a complex section consisting of n simplest figures, the coordinates of the center of gravity of the section are determined by the formulas |
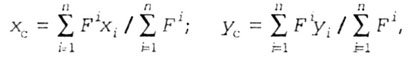 |
| where X j and Y j are the coordinates of the centers of gravity of individual section figures. |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials