Lecture
| STABILITY OF COMPRESSED RODS |
| Along with the problem of strength, there is the problem of structural stability. The study of the causes of the destruction of structures showed that for reliable operation of the structure under load it is not enough to make its elements durable, it is also necessary to ensure the preservation of the original balance of both the elements and the structure as a whole. |
| Consider a long thin rod (Fig. 8.1, a) loaded with an axial compressive force R. |
| In this case, two forms of rod equilibrium are possible: rectilinear and curvilinear. |
| At small values of the force P, the rod is compressed, remaining straight. If it is removed from the equilibrium position, then under the action of the elastic forces the rod, hesitating around the equilibrium position, will take the initial shape. In this case, the rectilinear form is stable (Fig. 8.1, a). |
| If we increase the compressive force P, then for some of its value the rod deflected from the vertical position will not return to the initial position to eliminate the cause that deflected it. |
| In this case, a stable is a curvilinear form of equilibrium (Fig. 8.1.6). |
| The value of the force at which the original equilibrium form of an elastic body becomes unstable is called the critical force. |
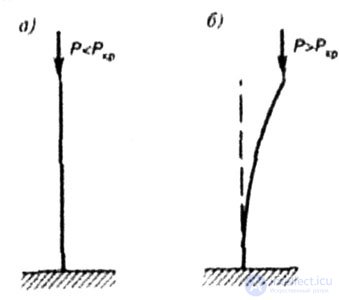 |
| Fig. 8.1 |
| The smallest value of the compressive force at which the compressed rod loses the ability to maintain a rectilinear form of stable equilibrium is also called a critical force and is denoted by P cr . |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials