Lecture
Linear stress state is experienced by some points of the rod working for bending or complex resistance, but in most cases this type of stress state is experienced by points of the rod working in tension or compression.
Consider a rod experiencing simple tension (Fig. 9.5, a). We calculate the stresses acting on any inclined section. We cut the rod by section  making an angle
making an angle  with cross section
with cross section 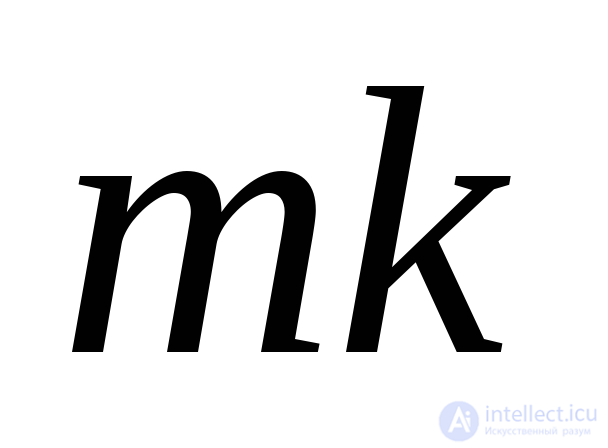 perpendicular to the axis of the rod. The same angle is made up of the normals to the transverse and inclined sections. For the positive direction of the reference angle
perpendicular to the axis of the rod. The same angle is made up of the normals to the transverse and inclined sections. For the positive direction of the reference angle  take the direction counterclockwise. The normal OA directed outward with respect to the cut off part of the rod will be called the external normal to the cross section
take the direction counterclockwise. The normal OA directed outward with respect to the cut off part of the rod will be called the external normal to the cross section  . Cross-sectional area
. Cross-sectional area 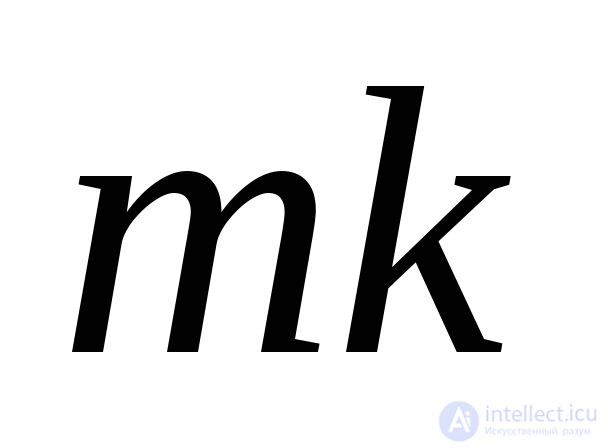 denote
denote  , cross-sectional area
, cross-sectional area  denote
denote 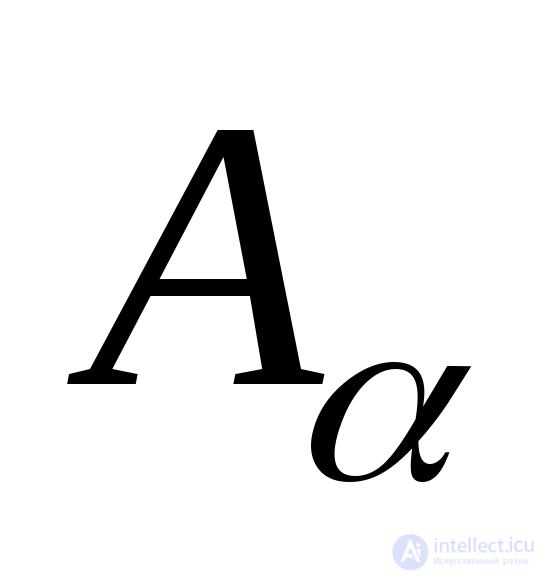 .
.
Mentally discard the upper part of the rod and replace its action with the lower part by stresses 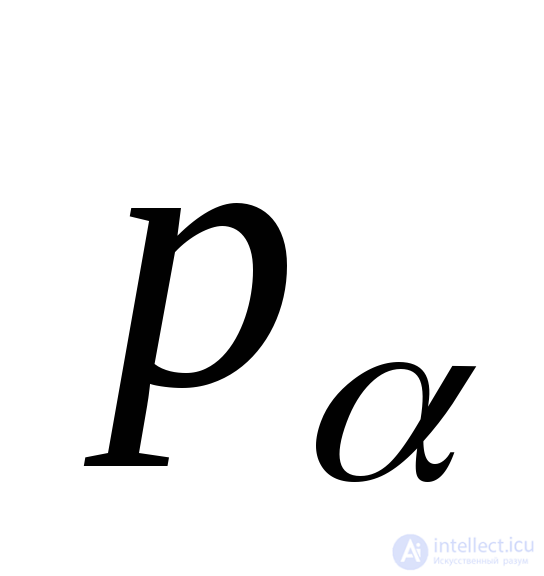 (Fig. 9.5b).
(Fig. 9.5b).
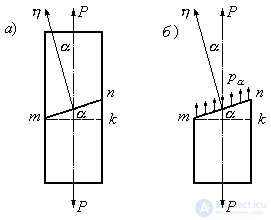
Fig.9.5
Accepting the hypothesis of flat sections, we assume that the stress 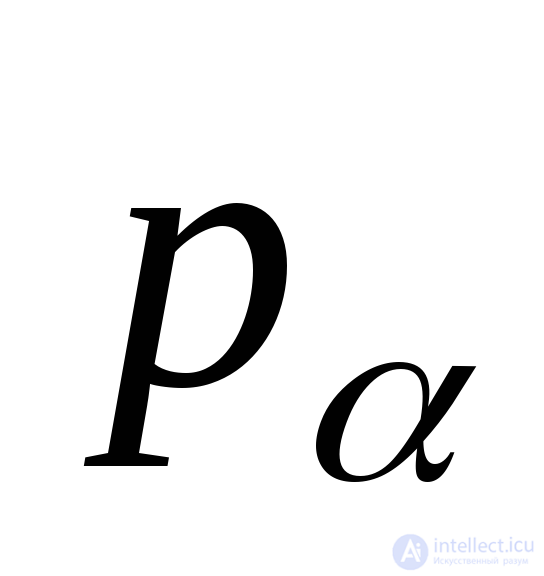 evenly distributed over the area
evenly distributed over the area 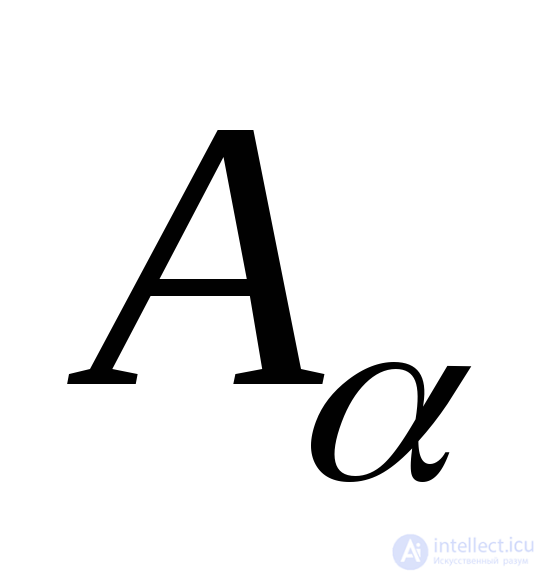 :
:
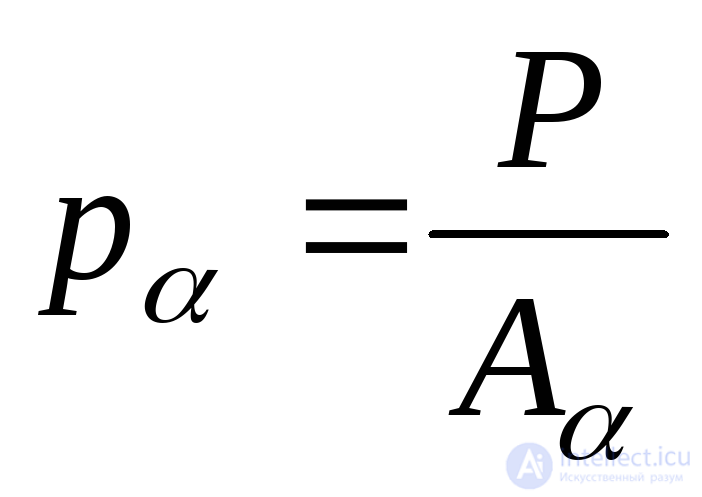 . (9.1)
. (9.1)
Given that 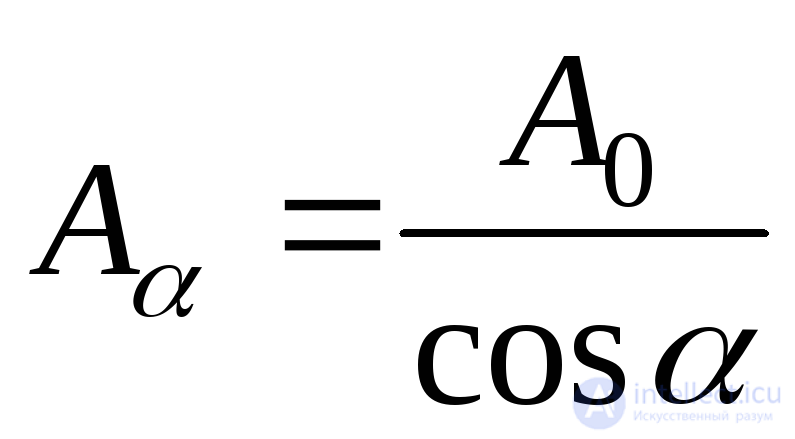 and substituting
and substituting 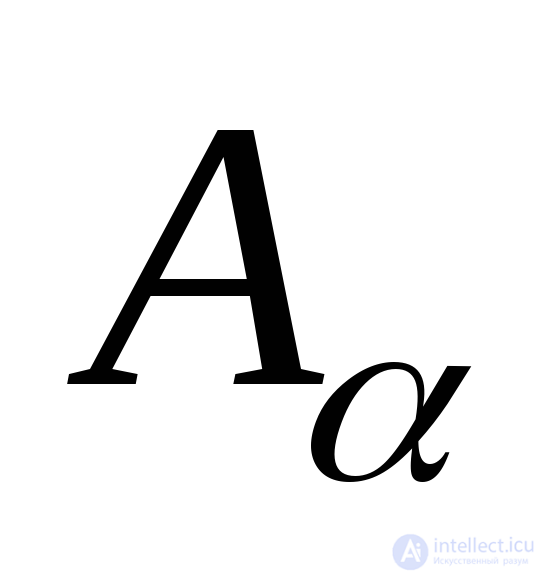 in (9.1), we obtain:
in (9.1), we obtain:
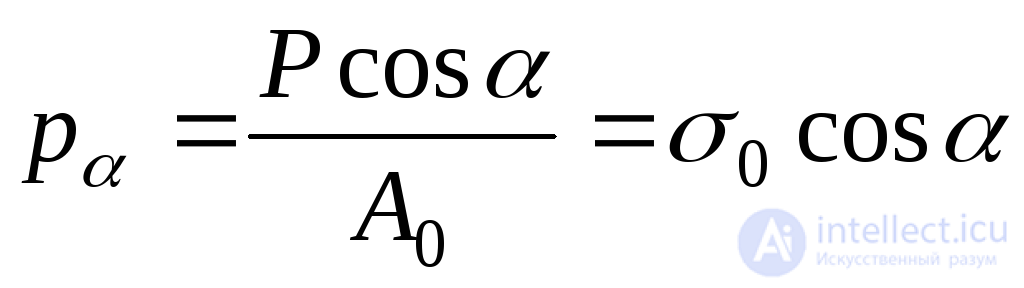 , (9.2)
, (9.2)
Where 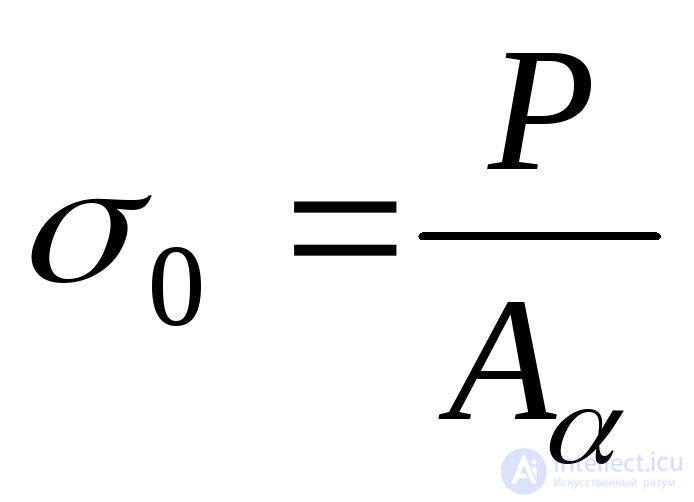 normal site voltage
normal site voltage 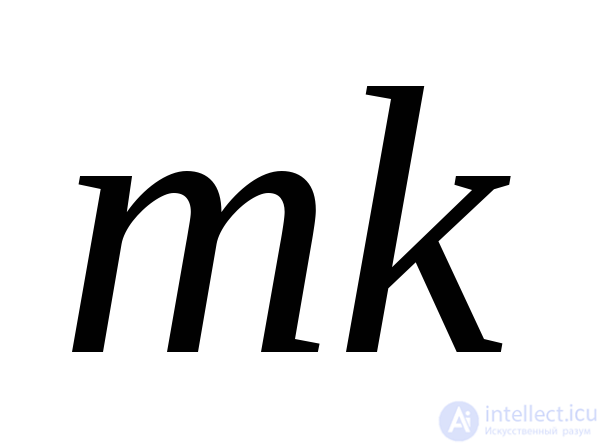 perpendicular to tensile force.
perpendicular to tensile force.
Designing 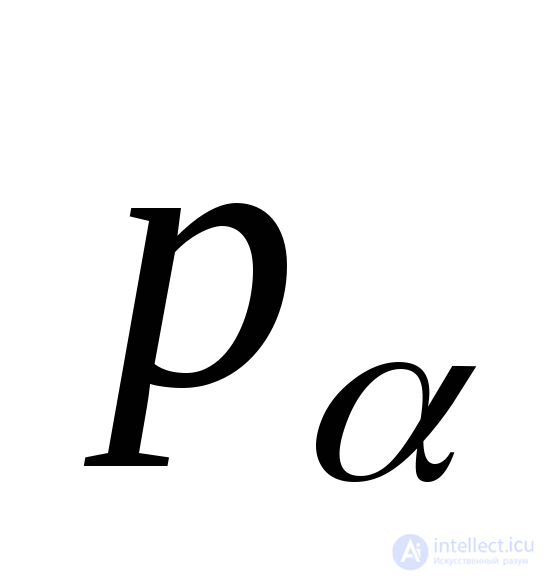 to normal
to normal 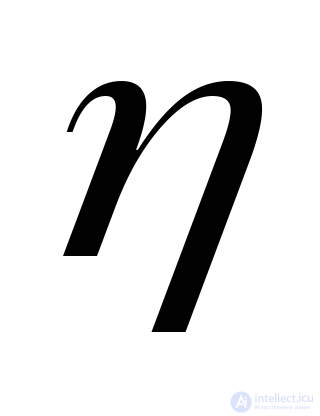 and on the section plane, we obtain the expressions for the normal and tangential stresses on the inclined platform:
and on the section plane, we obtain the expressions for the normal and tangential stresses on the inclined platform:
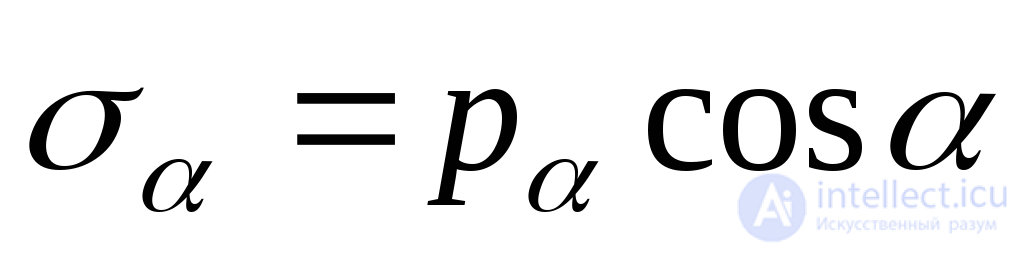 ;
;
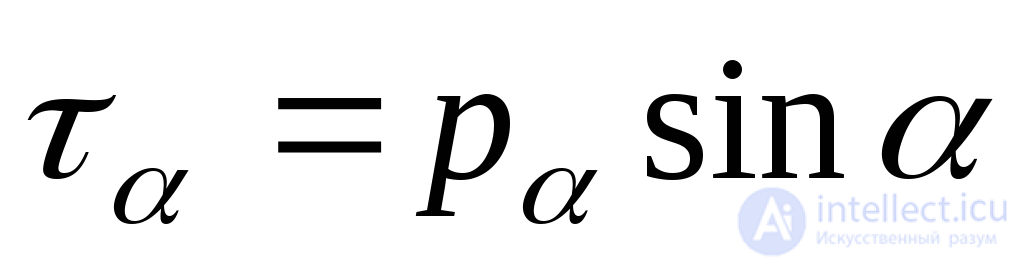
or
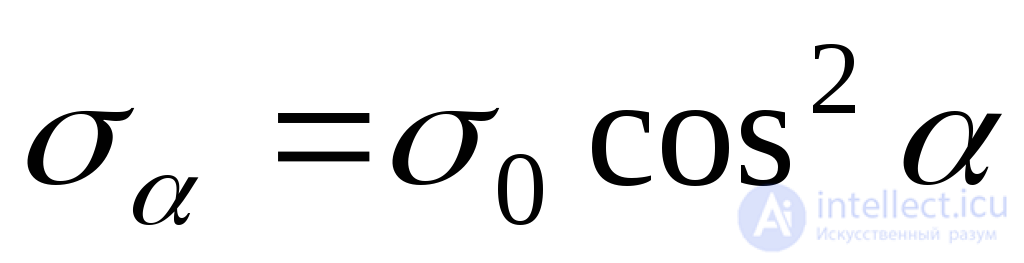 , (9.3)
, (9.3)
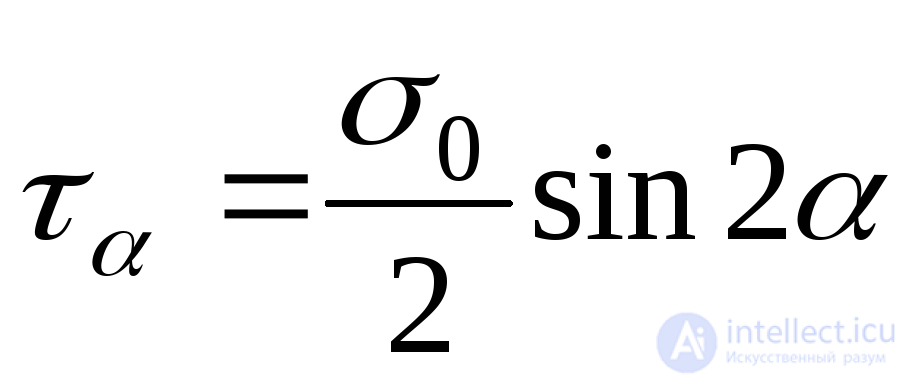 . (9.4)
. (9.4)
As can be seen from formulas (9.3) (9.4), for 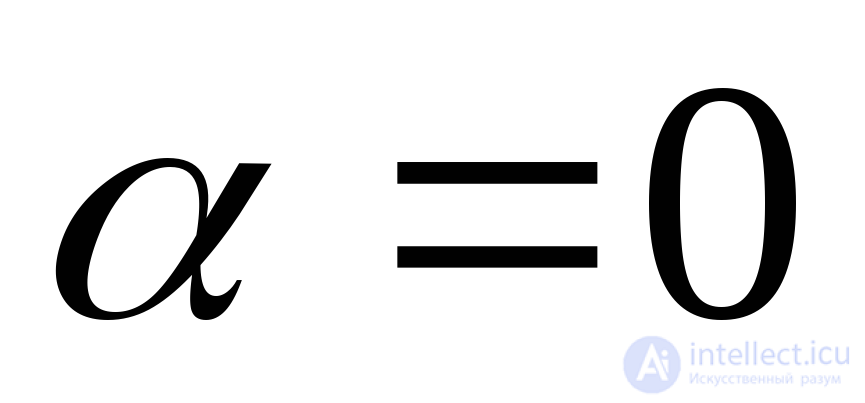 voltage
voltage  ,
, 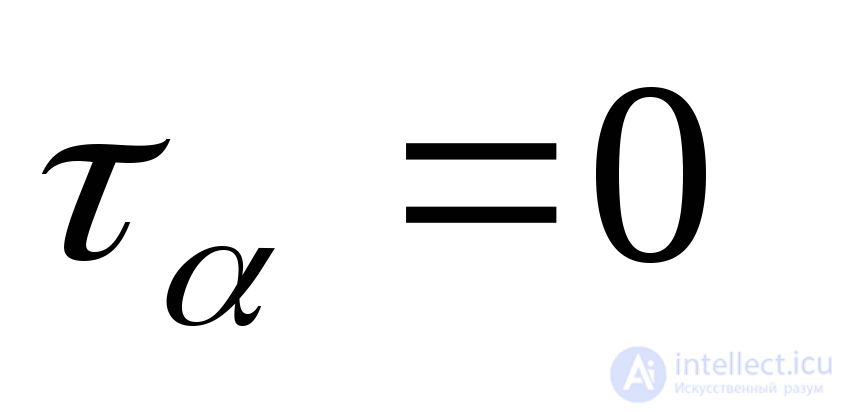 ; at
; at 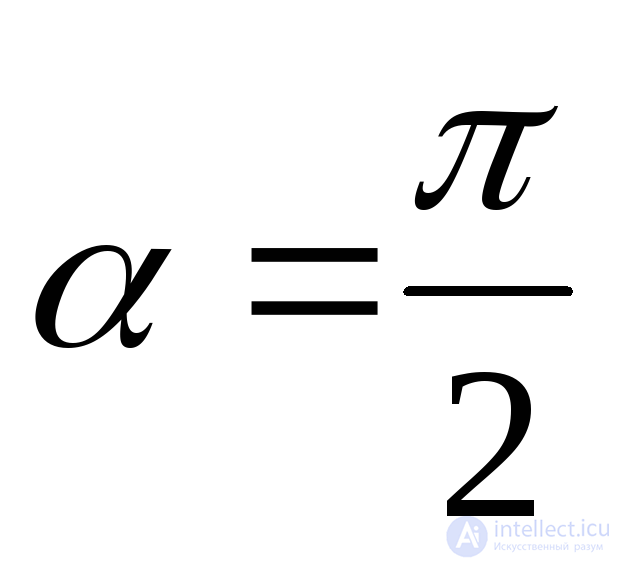 voltage
voltage  and
and 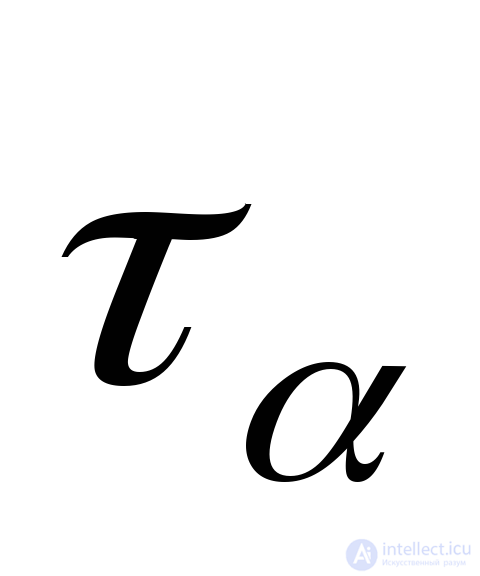
 are equal to zero (Fig. 9.6).
are equal to zero (Fig. 9.6).
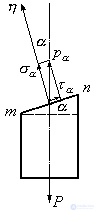
Figure 9.6
Thus, with simple tension and compression at each point of the body, the main areas are perpendicular and parallel to its axis, and the main stresses in it are respectively equal:
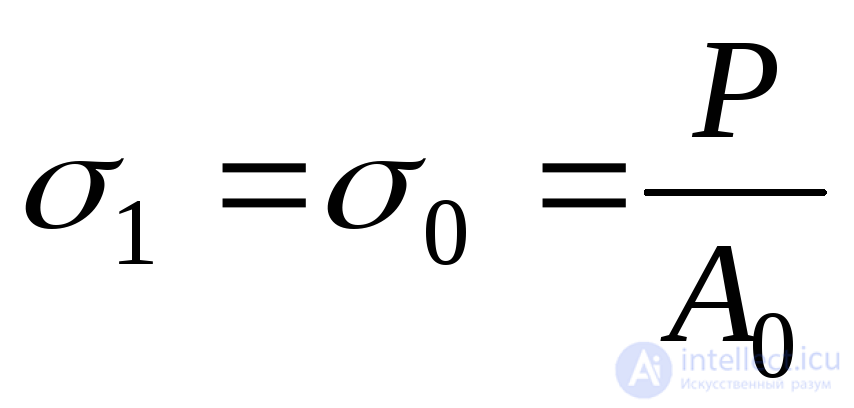 ;
; 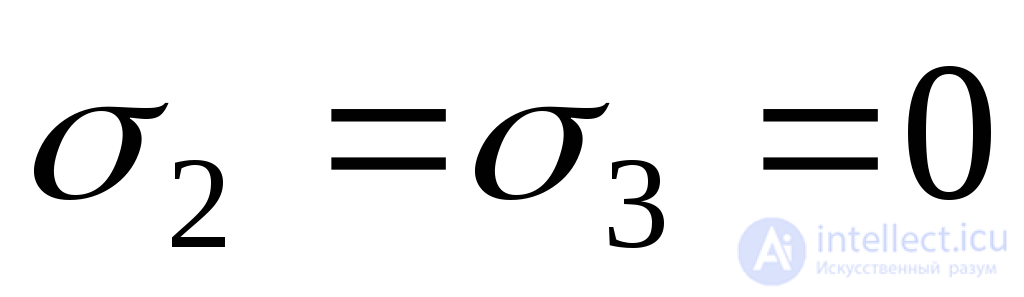 tensile
tensile
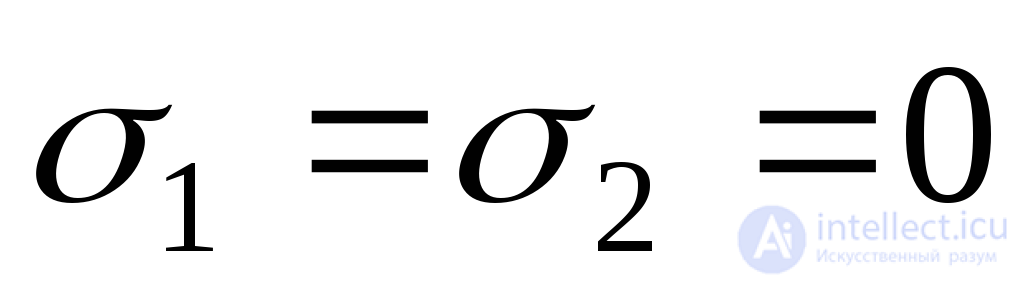 ;
; 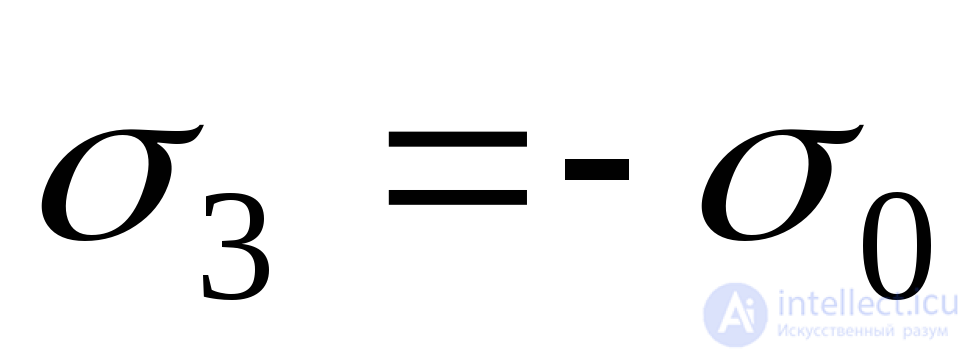 in compression.
in compression.
Maximum tangential stresses act in areas that are inclined to the main areas at an angle 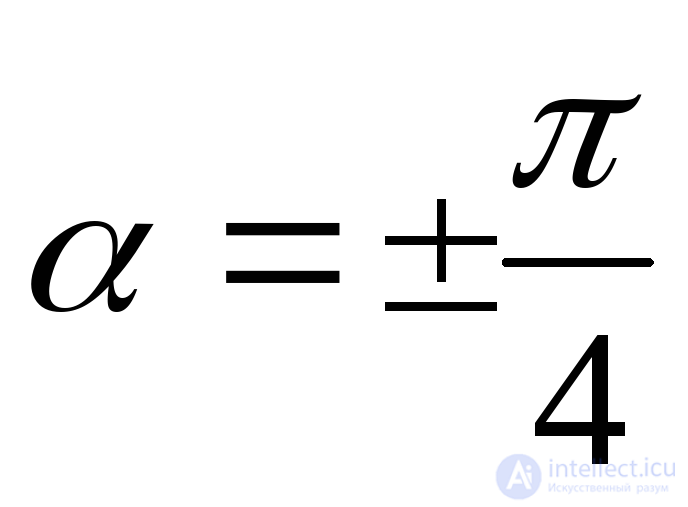 . Wherein
. Wherein
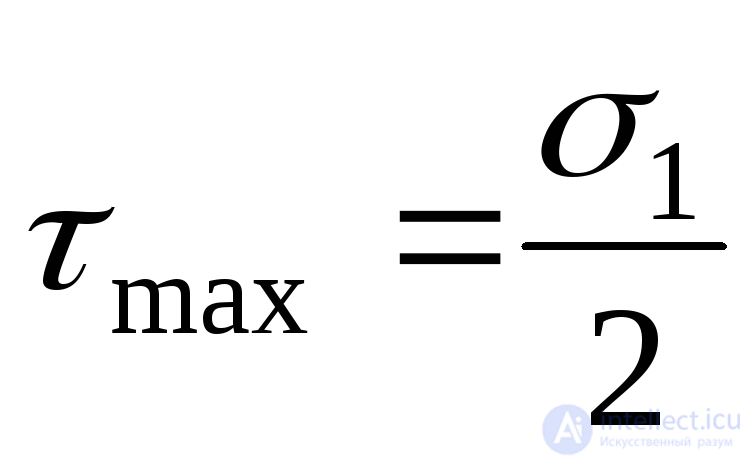 (9.5)
(9.5)
Example 9.1 Determine the normal and tangential stresses on inclined platforms for the elements shown in Fig. 9.7.
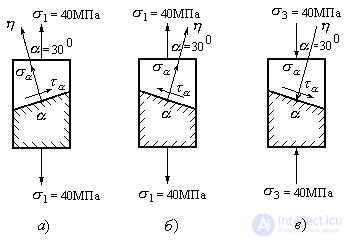
Decision:
For the element in Fig. 9.7, a: 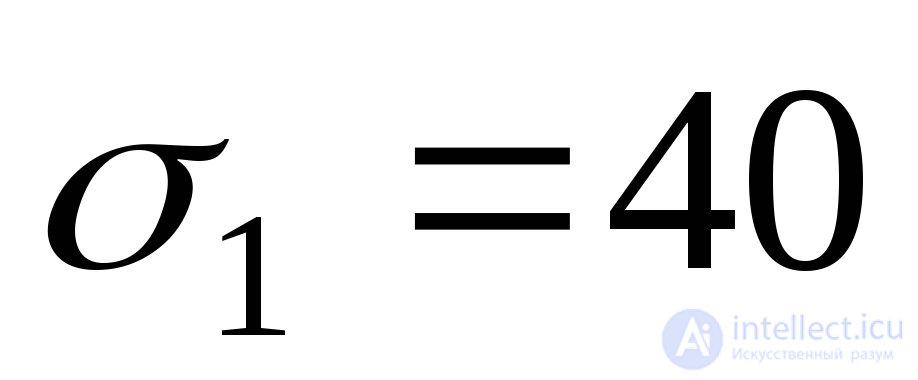 MPa;
MPa; 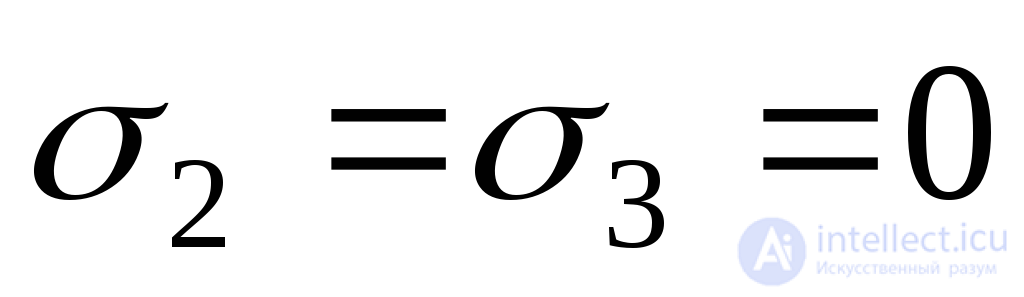 ;
; 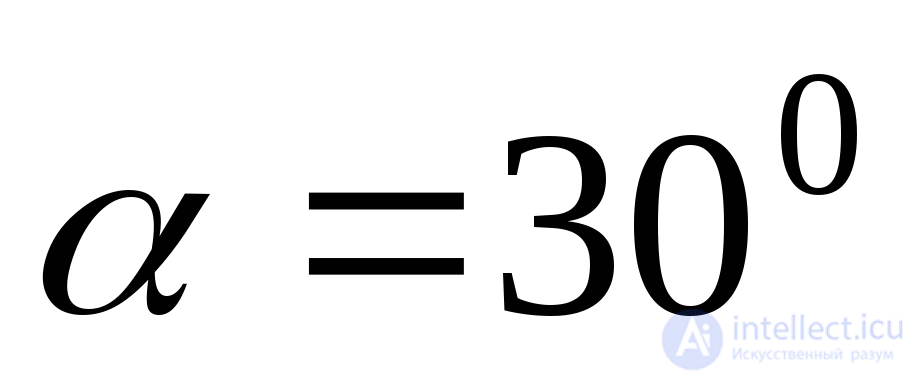 .
.
From: 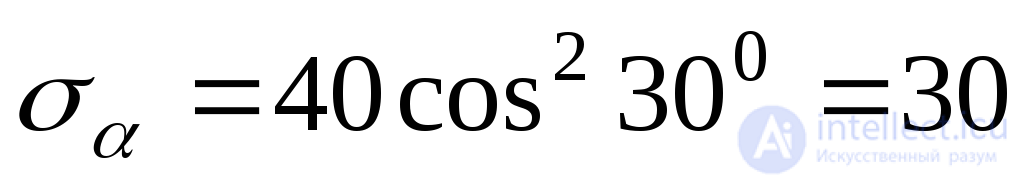 MPa;
MPa; 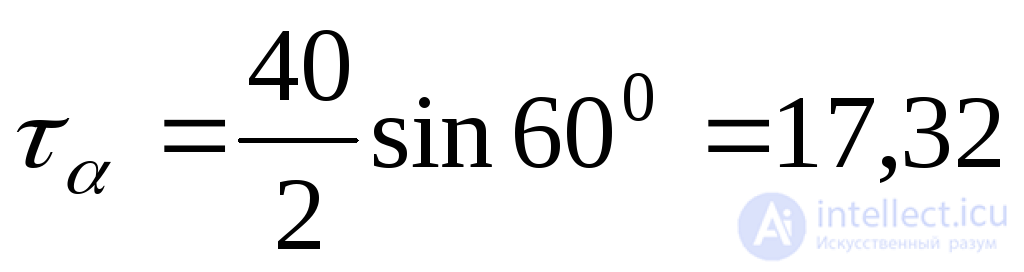 MPa
MPa
For the element in Fig. 9.7, b: 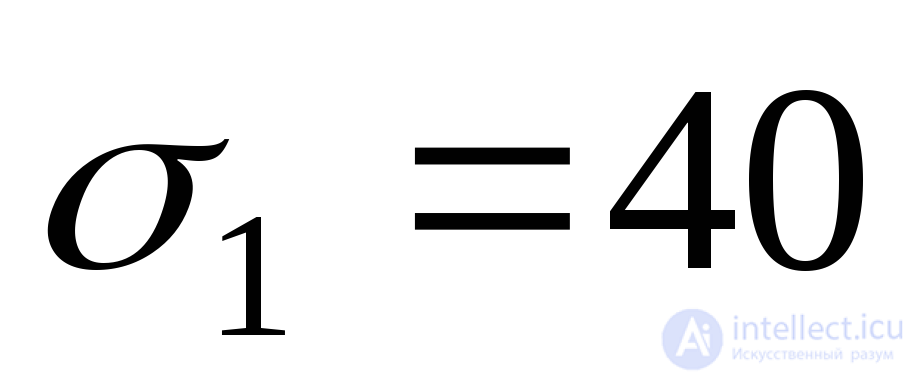 MPa;
MPa; 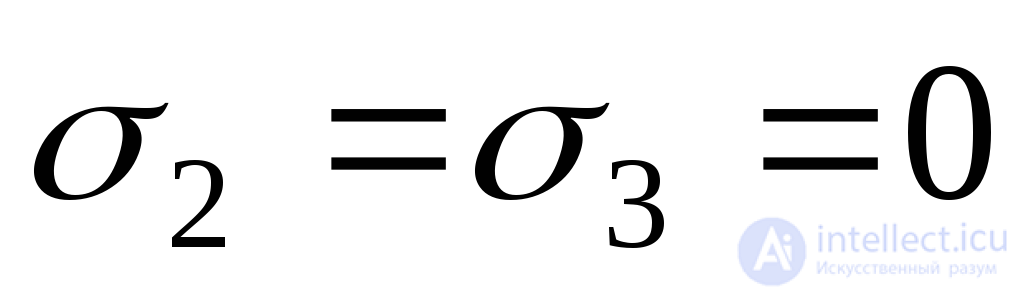 ;
; 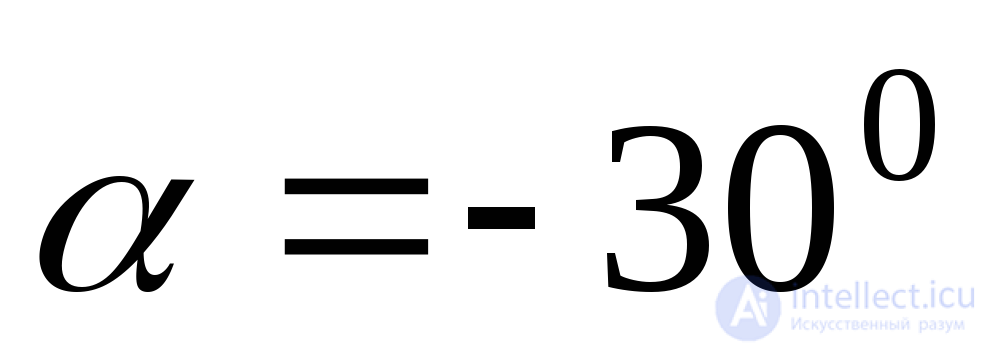 .
.
From: 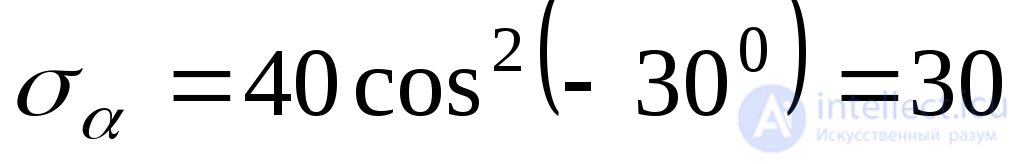 MPa;
MPa; 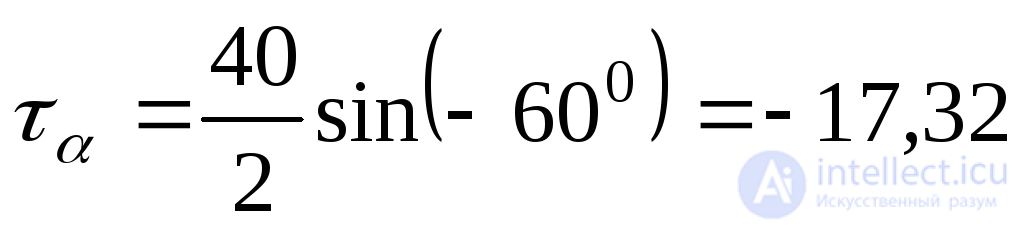 MPa
MPa
3. For the element in Fig. 9.7, c: 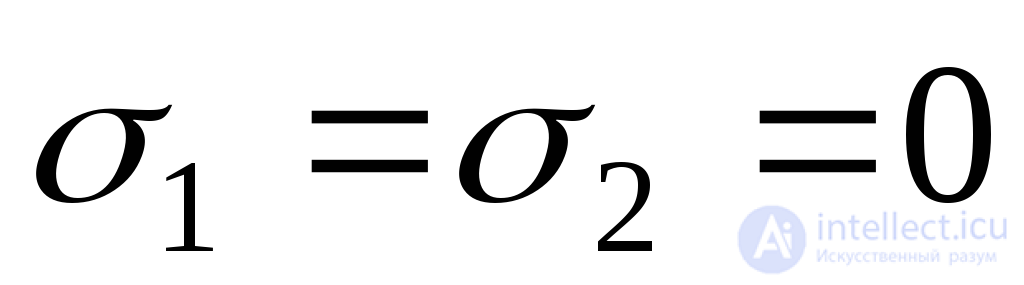 ;
;  MPa;
MPa; 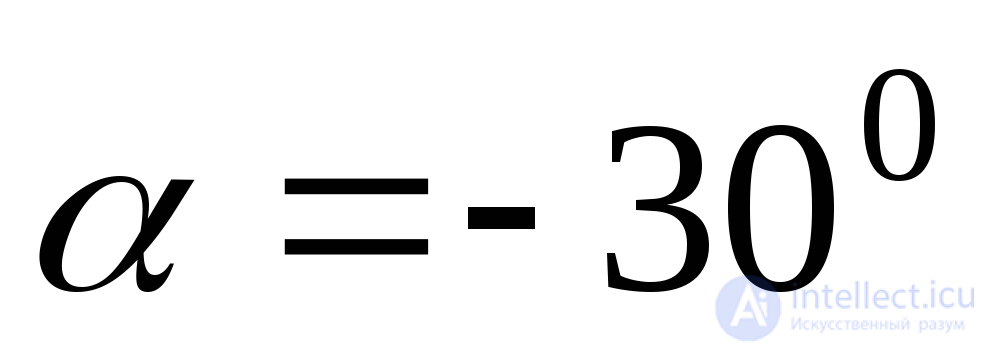 .
.
From: 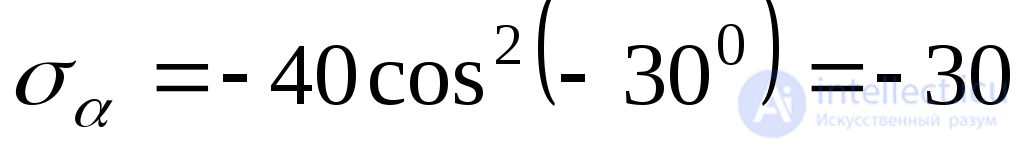 MPa;
MPa; 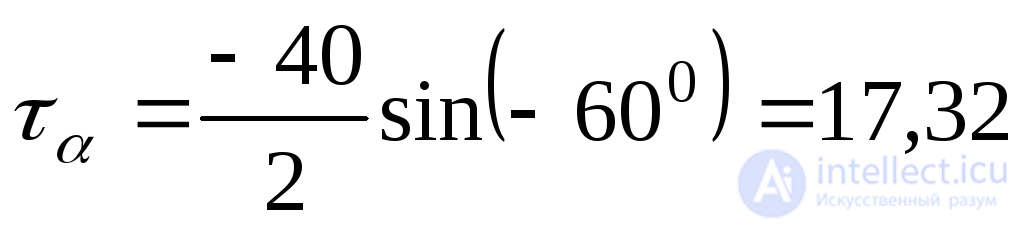 MPa
MPa
Comments
To leave a comment
Strength of materials
Terms: Strength of materials