Lecture
| The task of determining the greatest stresses begins with the search for a section in which the greatest internal forces act. |
| In the case of direct transverse bending of a cantilever beam loaded with a concentrated force P (Fig. 1.9), the greatest bending moment will be in section A at the embedment, since the maximum bending moment here is equal to M A = P * a. |
 |
| Fig. 1.9 |
| A dangerous section is a cross section in which the greatest internal forces act. |
| Where the dangerous section will be located in the more complicated loading case (Fig. 1.10) it is difficult to answer right away, since the concentrated bending moment M and the distributed load q bend the beam downwards, and the concentrated force P - upwards, while the moment values from each type of load are different . |
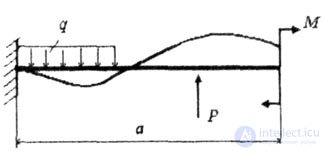 |
| Fig. 1.10 |
| Therefore, for complex cases of loading, it is necessary to know the law of variation along the beam length of a bending moment or other internal force (for example, the longitudinal force N, the lateral force Q or the torque M cr ). |
| This law can be depicted with the help of special graphs called diagrams. |
| Plot is a graph depicting the law of variation of internal force along a rod. Each ordinate of the plot represents the amount of force in the corresponding cross section of the rod. |
| Plotting by the method of sections is performed in four stages. |
| From the equation sections compiled at the fourth stage of the method, we express the sought internal force factors: N, Q x , Q y , M x , M y, and M z (M kr ). |
| Using the obtained expressions, we construct graphs of changes in the WSF - L /, Mx, etc. along the length of the rod - epures. |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials