Lecture
| Centrifugal Stretching (Compression) |
| This type of loading is called in which the resultant of external forces does not coincide with the axis of the rod, as in normal tension (compression), but is displaced relative to the longitudinal axis and remains parallel to it. |
| The axes X and Y are the central (S X = S Y = 0) and principal (I XY = 0) axes of inertia of the cross section. Normal stresses in the cross section from the action of a force P displaced relative to the center of gravity to point A with the coordinates X P and Y P (Fig. 7.2, a.b) are determined by the formula: |
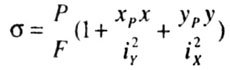 |
| R is the resultant of external or internal forces; |
| F is the cross-sectional area; |
| X P , Y P - coordinates of the point of application of force R. |
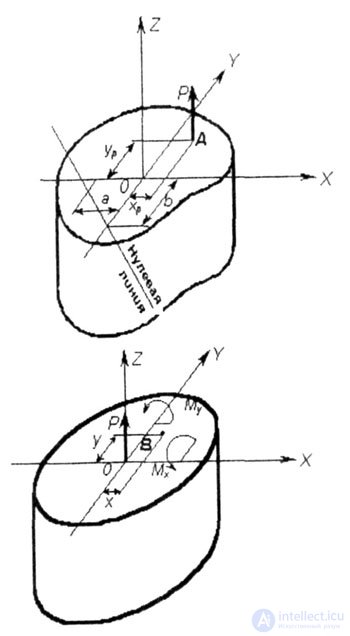
x, y - the current coordinates of the point at which the voltage is determined 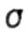 ; ; |
| i x , i y - the main radii of inertia of the cross section. |
 |
| Fig. 7.2 |
| The squares of the main radii of inertia are determined by the formulas: |
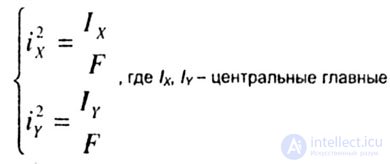 |
| moments of inertia of the cross section. Equation zero line. |
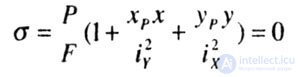 |
| Since P # 0, it follows from this expression |
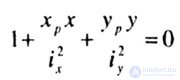 |
| The zero line is a straight line (Fig. 7.2, a). The points of intersection of the zero line with the axes of coordinates are determined by the expressions: |
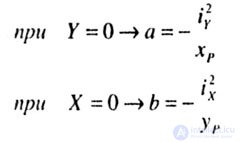 |
| The center of pressure is the point of intersection of the resultant external or internal forces with the plane of the cross section. |
| (In Fig. 7.2, and the center of pressure is point A.) |
| When designing structures and various types of supports made of concrete, brickwork, cast iron and other materials that do not work well in tension, the main requirement is the absence of tensile stresses. The solution of the problem is based on the property of the section kernel. |
| The core of a section is a part of the cross sectional plane located in the vicinity of the center of gravity satisfying the condition: if the center of pressure is located inside or on the boundary of the section core, then at any point of the cross section with current coordinates (x, y), stresses of the same sign occur. |
| In order for stresses of the same sign to appear in the cross section, the zero line must be located either outside the cross section or be tangent to the cross section, which is used in determining the boundaries of the core section. |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials