You get a bonus - 1 coin for daily activity. Now you have 1 coin

DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr).

Lecture



DETERMINATION OF CRITICAL FORCE WITH THE HELP OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Pcr ).
If the length reduction factor is not obvious, then Pcr can be found by solving a differential equation - this is an exact method for determining the critical force.
The peculiarity of stability problems is the fact that the rod equilibrium is considered in a deformed state, while in other sections equilibrium equations are compiled for an element of a loaded rod (or other body) without a section of its changes due to deformations.
General procedure for calculation:
  1. to depict the rod in the deformed state after loss of stability; discarding the supports, replace them with reactions (these reactions are unknown, we depict them in general form);
  2. selecting the coordinate axes, apply the section method by sections; in a section to apply all internal total power factors, having directed them to the positive side;
  3. write the equilibrium equation of the cut part of the rod as a sum of moments relative to the X axis of an arbitrary section;
  4. replacing the bending moment through curvature and stiffness
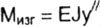DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr).
we obtain differential equilibrium equations in an amount equal to the number of sections (in this case we denote 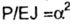DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr). );
Using the boundary conditions at the ends of the rod and the conditions for joining the sections (equality of displacements and rotation angles at the end of the previous and the beginning of the next section, since the curved axis of the rod is a smooth curve without breaks and breaks), we obtain the so-called characteristic equation.
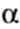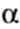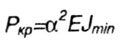Solving the obtained (most often transcendental) equation by selection, graphically or using a computer, we obtain a series of values DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr). satisfying the equation and boundary conditions of the problem. The smallest (non-zero) of the values ​​obtained DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr). gives expression to the critical force in the form
DETERMINATION OF CRITICAL POWER BY MEANS OF A DIFFERENTIAL EQUATION (EXACT METHOD OF DEFINITION Rcr).

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Strength of materials

Terms: Strength of materials