Lecture
| Due to the difficulty of integrating the differential equation of the elastic line of a rod, various approximate methods for determining the critical force are often used. One of such methods is energy based on the study of changes in potential energy during the transition of a rod from a straight to a curvilinear form of equilibrium. |
| Since critical is the value of the force compressing the rod, at which both the rectilinear and infinitely close to it curvilinear forms of stable equilibrium are equally possible, according to fig. 8.4 forms of equilibrium I and II are equivalent and when moving from state I to state II there is no change in the energy of the system in this case of indifferent equilibrium, i.e. |
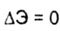 |
| where the change in the total potential energy of the system consists of a decrease in the potential of the force P during the transition from state I to state II and the acquisition of the potential bending energy in state II. From here |
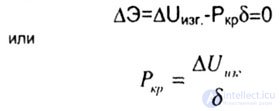 |
| Bending strain potential energy |
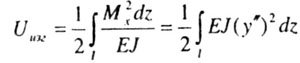 |
| Moving the point of application of force P |
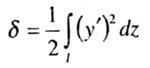 |
| From these expressions we get |
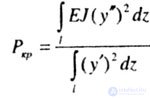 |
| Since in the numerator of this expression is a quantity proportional to the potential energy of bending deformations, the integral in the numerator is taken along the entire length of the rod bent with a loss of stability. If there are areas of different stiffness E, J, then one should take the sum of the integrals over all n areas |
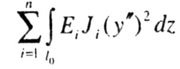 |
| The denominator of the expression for Rcr is a quantity proportional to the displacement of the point of application of the load. If there are several longitudinal forces acting on the rod, then each jth force (P j ) must be multiplied by the displacement of its application point) |
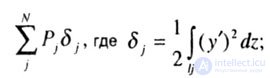 |
| here I j is the distance from the point of application of the compressive force to the lower support, i.e. the length of the area compressed by this force; N is the number I of longitudinal forces. |
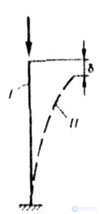 |
| Fig. 8.4 |
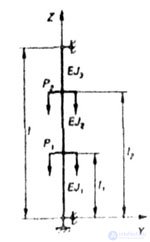 |
| Fig. 8.5 |
| So, for example, for the rod shown in fig. 8.5, the energy balance would look like: |
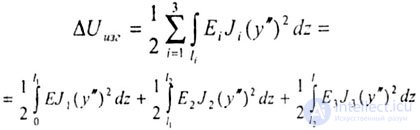 |
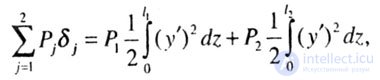 |
| where n is the number of sections of different stiffness, here n = 3. |
| In all these expressions, y = f (z) is the function of the deflections, which we select (therefore, an approximate method) taking into account the boundary conditions. This may be, for example, a trigonometric expression, an algebraic expression, or a polynomial whose degree is equal to the number of boundary conditions. If the function y = f (z) corresponds to the true shape of the curved axis, then the solution will be exact. |
| Analyzing the boundary conditions, it follows, having depicted the rod in the state deformed after loss of stability, to carry out necessarily the coordinate axes and think about these coordinate axes, where they will be zero: |
| y - moving, |
| I I - the angle of rotation of the axis of the rod, |
| II I has curvature, i.e. quantity proportional to the bending moment. |
| The last boundary condition (according to I I ) usually causes the greatest difficulties. The basic idea: since the bending moment is proportional to the curvature of the beam axis for I I , then I I is equal to the nupu where the bending moment is zero, these are the free and hingedly supported ends of the rod. |
| Attention should be paid to the fact that on the intermediate hinge support, in the general case, I I # 0 (since there is not a bending moment there). |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials