Lecture
Это окончание невероятной информации про статические структуры данных.
...
else {no space in the tree} if (bf and (x
Bitwise digital sorting.
The algorithm requires that the keys of the sorted sequence be represented as numbers in some number system P. The number of passes the sort is equal to the maximum number of significant digits in the number D. In each pass, the significant number in the next key discharge is analyzed, starting with the least significant digit. All keys with the same value of this digit are combined into one group. The keys in the group are arranged in the order they are received. After the entire initial sequence is distributed into groups, the groups are arranged in ascending order of the numbers associated with the groups. The process is repeated for the second digit, etc., until the significant digits in the key are exhausted. Основание системы счисления P может быть любым, в частном случае 2 или 10. Для системы счисления с основанием P требуется P групп.
Порядок алгоритма качественно линейный - O(N), для сортировки требуется D*N операций анализа цифры. Однако, в такой оценке порядка не учитывается ряд обстоятельств.
Во-первых, операция выделения значащей цифры будет простой и быстрой только при P=2, для других систем счисления эта операция может оказаться значительно более времяемкой, чем операция сравнения.
Во-вторых, в оценке алгоритма не учитываются расходы времени и памяти на создание и ведение групп. Размещение групп в статической рабочей памяти потребует памяти для P*N элементов, так как в предельном случае все элементы могут попасть в какую-то одну группу. Если же формировать группы внутри той же последовательности по принципу обменных алгоритмов, то возникает необходимость перераспределения последовательности между группами и все проблемы и недостатки, присущие алгоритмам включения. Наиболее рациональным является формирование групп в виде связных списков с динамическим выделением памяти.
В программном примере 3.15 мы, однако, применяем поразрядную сортировку к статической структуре данных и формируем группы на том же месте, где расположена исходная последовательность. Пример требует некоторых пояснений.
Область памяти, занимаемая массивом перераспределяется между входным и выходным множествами, как это делалось и в ряде предыдущих примеров. Выходное множество (оно размещается в начале массива) разбивается на группы. Разбиение отслеживается в массиве b. Элемент массива b[i] содержит индекс в массиве a,с которого начинается i+1-ая группа. Номер группы определяется значением анали- зируемой цифры числа, поэтому индексация в массиве b начинается с 0. Когда очередное число выбирается из входного множества и должно быть занесено в i-ую группу выходного множества, оно будет записано в позицию, определяемую значением b[i]. Но предварительно эта позиция должна быть освобождена: участок массива от b[i] до конца выходного множества включительно сдвигается вправо. После записи числа в i-ую группу i-ое и все последующие значения в массиве b корректируются - увеличиваются на 1.
{===== Программный пример 3.15 =====}
{ Цифровая сортировка (распределение) }
const D=...; { максимальное количество цифр в числе }
P=...; { основание системы счисления }
Function Digit(v, n : integer) : integer;
{ возвращает значение n-ой цифры в числе v }
begin
for n:=n downto 2 do v:=v div P;
Digit:=v mod P;
end;
Procedure Sort(var a : Seq);
Var b : array[0..P-2] of integer; { индекс элемента,
следующего за последним в i-ой группе }
i, j, k, m, x : integer;
begin
for m:=1 to D do begin { перебор цифр, начиная с младшей }
for i:=0 to P-2 do b[i]:=1; { нач. значения индексов }
for i:=1 to N do begin { перебор массива }
k:=Digit(a[i],m); { определение m-ой цифры }
x:=a[i];
{ сдвиг - освобождение места в конце k-ой группы }
for j:=i downto b[k]+1 do a[j]:=a[j-1];
{ запись в конец k-ой группы }
a[b[k]]:=x;
{ модификация k-го индекса и всех больших }
for j:=k to P-2 do b[j]:=b[j]+1;
end;
end;
Результаты трассировки программного примера 3.15 при P=10 и D=4 представлены в таблице 3.9.

Таблица 3.9
Быстрая сортировка Хоара.
Данный алгоритм относится к распределительным и обеспечивает показатели эффективности O(N*log2(N)) даже при наихудшем исходном распределении.
Используются два индекса - i и j - с начальными значениями 1 и N соответственно. Ключ K[i] сравнивается с ключом K[j]. Если ключи удовлетворяют критерию упорядоченности, то индекс j уменьшается на 1 и производится следующее сравнение. Если ключи не удовлетворяют критерию, то записи R[i] и R[j] меняются местами. При этом индекс j фиксируется и начинает меняться индекс i(увеличиваться на 1 после каждого сравнения). После следующей перестановки фиксируется i и начинает изменяться j и т.д. Проход заканчивается, когда индексы i и j становятся равными. Запись, находящаяся на позиции встречи индексов, стоит на своем месте в последовательности. Эта запись делит последовательность на два подмножества. Все записи, расположенные слева от нее имеют ключи, меньшие чем ключ этой записи, все записи справа - большие. Тот же самый алгоритм применяется к левому подмножеству, а затем к правому. Записи подмножества распределяются по двум еще меньшим подмножествам и т.д., и т.д. Распределение заканчивается, когда полученное подмножество будет состоять из единственного элемента - такое подмножество уже является упорядоченным.
Процедура сортировки в примере 3.16 рекурсивная. При ее вызове должны быть заданы значения границ сортируемого участка от 1 до N.
{===== Программный пример 3.16 =====}
{ Быстрая сортировка Хоара }
Procedure Sort(var a : Seq; i0,j0 : integer);
{ i0, j0 - границы сортируемого участка }
Var i, j : integer; { текущие индексы в массиве }
flag : boolean; { признак меняющегося индекса: если
flag=true - уменьшается j, иначе - увеличивается i }
x : integer;
begin
if j0 <= i0 Exit; { подмножество пустое или из 1 эл-та }
i:=i0; j:=j0;
flag:=true; { вначале будет изменяться j }
while i < j do begin
if a[i] > a[j] then begin
x:=a[i]; a[i]:=a[j]; a[j]:=x; { перестановка }
{ после перестановки меняется изменяемый индекс }
flag:= not flag;
end;
{ реально изменяется только один индекс }
if flag then j:=j-1 else i:=i+1;
end;
Sort(a,i0,i-1); { сортировка левого подмассива }
Sort(a,i+1,j0); { сортировка правого подмассива }
end;
Результаты трассировки примера приведены в таблице 3.10. В каждой строке таблицы показаны текущие положения индексов i и j, звездочками отмечены элементы, ставшие на свои места. Для каждого прохода показаны границы подмножества, в котором ведется сортировка.
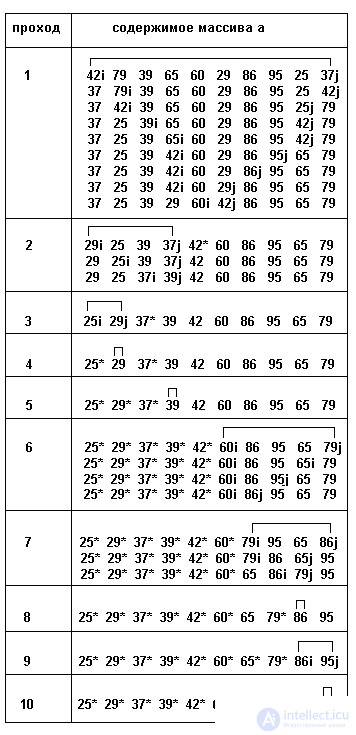
Таблица 3.10
Алгоритмы сортировки слиянием, как правило, имеют порядок O(N*log2(N)), но отличаются от других алгоритмов большей сложностью и требуют большого числа пересылок. Алгоритмы слияния применяются в основном, как составная часть внеш- ней сортировки, которая более подробно будет рассматриваться нами во втором томе нашего пособия. Здесь же для понимания принципа слияния мы приводим простейший алгоритм слияния в оперативной памяти.
Сортировка попарным слиянием.
Входное множество рассматривается, как последовательность подмножеств, каждое из которых состоит из единственного элемента и, следовательно, является уже упорядоченным. На первом проходе каждые два соседних одно-элементных множества сливаются в одно двух-элементное упорядоченное множество. На втором проходе двух-элементные множества сливаются в 4-элементные упорядоченные множества и т.д. В конце концов мы получаем одно большое упорядоченное множество.
Важнейшей частью алгоритма является слияние двух упорядоченных множеств. Эту часть алгоритма мы опишем строго.
Программный пример 3.17 иллюстрирует сортировку попарным слиянием в ее обменном варианте - выходные множества формируются на месте входных.
{===== Программный пример 3.17 =====}
{ Сортировка слиянием }
Procedure Sort(var a :Seq);
Var i0,j0,i,j,si,sj,k,ke,t,m : integer;
begin
si:=1; { начальный размер одного множества }
while si < N do begin
{ цикл пока одно множество не составит весь массив }
i0:=1; { нач. индекс 1-го множества пары }
while i0 < N do begin
{ цикл пока не пересмотрим весь массив }
j0:=i0+si; { нач. индекс 2-го множества пары }
i:=i0; j:=j0;
{ размер 2-го множества пары может ограничиваться
концом массива }
if si > N-j0+1 then sj:=N-j0+1 else sj:=si;
if sj > 0 then begin
k:=i0; { нач. индекс слитого множества }
while (i < i0+si+sj) and (j a[j] then begin
{ если эл-т 1-го <= элемента 2-го, он остается на
своем месте, но вых.множество расширяется иначе -
освобождается место в вых.множестве и туда заносится
эл-т из 2-го множества }
t:=a[j];
for m:=j-1 downto k do a[m+1]:=a[m];
a[k]:=t;
j: = j + 1; { к след. эл-ту во 2-м множестве }
end; { if a[i] > a[j] }
k:=k+1; { вых. множество увеличилось }
i: = i + 1; { если был перенос - за счет сдвига, если
не было - за счет перехода эл-та в вых. }
end; { while }
end; { if sj > 0 }
i0:=i0+si*2; { начало следующей пары }
end; { while i0 < N }
si:=si*2; { размер эл-тов пары увеличивается вдвое }
end; { while si < N }
end;
Результаты трассировки примера приведены в таблице 3.11. Для каждого прохода показаны множества, которые на этом проходе сливаются. Обратите внимание на обработку последнего множества, оставшегося без пары.
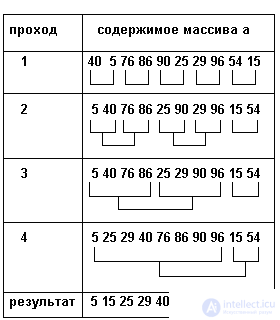
Таблица 3.11
Часть 1 3. STATIC DATA STRUCTURE
Часть 2 3.8. Операции логического уровня над статическими структурами. Sorting - 3.
Часть 3 3.8.3. Sort by distribution. - 3. STATIC DATA STRUCTURE
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.