Lecture
Simple data structures are also called primitive or basic structures. These structures serve as the basis for building more complex structures. In programming languages, simple structures are described by simple (basic) types. These types include: numeric, bit, logical, character, enumerated, interval, pointers. In the following, we focus mainly on the PASCAL language and its implementation in the MS DOS environment. The structure of simple PASCAL types is shown in Figure 2.1 (comma-separated memory size in bytes is required to accommodate data of the appropriate type). In other programming languages, the set of simple types may differ slightly from that indicated. The size of the memory required for data of one type or another may be different not only in different programming languages, but also in different implementations of the same language.
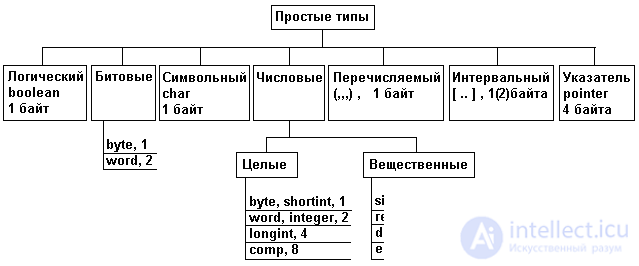
Fig. 2.1. The structure of simple types PASCAL.
With the help of integers, the number of objects that are discrete in nature (that is, a countable number of objects) can be represented.
Presentation in memory.
To represent signed numbers in a number of computers, a method called the sign and value method was used. Usually the first (or left-most) bit of a binary number is assigned to a character, followed by the entry of the number itself.
For example, +10 and -15 in binary form can be represented as follows:
| Number | Sign bit | Magnitude |
| +10 | 0 | 0001010 |
| -15 | one | 0001111 |
Note that by convention, 0 is used to represent the plus sign and 1 for the minus. Such a presentation is convenient for programmers. easily perceived, but not economical.
If you want to add or subtract two numbers, then in order to decide what actions to take, you must first determine the sign of each number. For example, the addition of the numbers +6 and -7 actually implies the operation of subtraction, and the subtraction of -6 from the +7 addition operation. For the analysis of the sign bit, a special scheme is required and, moreover, when representing numbers as signs and values, separate devices are needed for addition and subtraction, that is, if the positive and negative numbers are represented in the direct code, operations on the character codes are performed separately. Therefore, the representation of numbers in the form of a sign and meaning is not widely used.
At the same time, using the inverse and additional codes used to represent negative numbers, the subtraction (algebraic addition) operation is reduced to the simple arithmetic addition operation. In this case, the addition operation extends to the digits of the characters considered as digits of the integer part of the number. That is why an additional code is used to represent signed integers.
The additional code of a negative number is formed according to the following rules:
For example, for the number -33 in integer format:
1000000000100001 direct code
0111111111011110 reverse code
+ _______________ 1
1111111111011111 additional code
For positive numbers, the forward, reverse, and optional codes are the same. Integrals in the format shortint, longint, comp are presented in the same way.
When developing programs at the stage of selecting the type of data, it is important to know the range of integer values that can be stored in n bits of memory. In accordance with the algorithm for converting binary numbers to decimal, the summation formula for n digits is:
n-1
2 ^ 0 + 2 ^ 1 + 2 ^ 3 + ... + 2 ^ (n-1), or SUM (2 ^ i) = 2 ^ n - 1.
i = 0
With n-bit storage of a number in the additional code, the first bit expresses the sign of the integer. Therefore, positive numbers are represented in the range from 0 to 1 * 2 ^ 0 + 1 * 2 ^ 1 + ... + 1 * 2 ^ (n-2) or from 0 to 2 ^ (n-1) - 1. All others configurations of bits express negative numbers in the range from -2 ^ (n-1) to -1. Thus, we can say that the number N can be stored in n bits of memory, if its value is in the range:
-2 ^ (n-1) <= N <= 2 ^ (n-1) - 1.
| Type of | Value range | Machine presentation |
| shortint | -128..127 | 8 bits, with a sign |
| integer | -32768..32767 | 16 bits, with a sign |
| longint | -2147483648..2147483647 | 32 bits, with a sign |
| byte | 0..255 | 8 bits unsigned |
| word | 0..65535 | 16 bits unsigned |
| comp | -2 ^ 63 + 1..2 ^ 63-1 | 64 bits with a sign |
Table 2.1
In other words, the range of possible values of integer types depends on their internal representation, which can take 1, 2 or 4 bytes. Table 2.1 provides a list of integer types, the size of the memory for their internal representation in bits, the range of possible values.
Machine representation of unsigned types.
The unsigned types in PASCAL include the BYTE and WORD types.
The format of machine representation of numbers of type BYTE is shown in Figure 2.2. but).
For example: 1). Machine representation of the number 45:
45 = 2 ^ 5 + 2 ^ 3 + 2 ^ 2 + 2 ^ 0 = 00101101
2). Machine representation of the boundaries of the range
valid values of numbers 0 and 255:
0: 00000000; 255: 11111111.

Fig. 2.2. Machine representation format of unsigned numbers
The format of machine representation of numbers of type WORD is shown in Fig. 2.2. b).
For example: 1). Machine number representation 258:
257 = 2 ^ 8 + 2 ^ 1 = 00000010 00000001.
2). Machine representation of boundaries:
0: 00000000 00000000; 65535: 11111111 11111111.
Machine representation of signed numbers.
The following types of SHORTINT, INTEGER, LONGINT are defined for representing signed numbers. In these types of numbers are stored in an additional code. Recall that the additional code of positive numbers coincides with the direct code.
The format of machine representation of numbers of type SHORTINT is shown in Figure 2.3. a) where s is the sign digit of the number. For positive numbers s = 0, for negative s = 1.
For example, the machine representation of numbers in the format of shortint:
one). 0: 00000000;
2). +127: 01111111;
3). -128: 10,000,000.
The format of machine representation of numbers of type INTEGER is shown in Figure 2.3. b). For example:
one). +32765: 11111101 01111111;
2). -32765: 00000011 10,000,000;
3). -47: 11010001 11111111.
Machine representation of the range of acceptable values:
four). -32768: 00000000 10,000,000;
five). 32767: 11111111 01111111.
The format of machine representation of LONGINT numbers is shown in Figure 2.3. at). For example, the representation of numbers in longint format:
one). +89 01011001 00000000 00000000 00000000;
2). -89 10100111 11111111 11111111 11111111.
Machine data representation type COMP. . 0 Type COMP is designed to work with large integers (see table 2.1). Therefore, the numbers of this type are represented in memory in accordance with the rules for the representation of signed integers - in the additional code. But for the convenience of users when entering and outputting the values of numbers in this format, it is allowed to use the form of recording numbers characteristic of real numbers (in the form of a mantissa and order).
For example: machine representation of numbers in COMP format:
+512 0..0 00000010 0..0 0..0 0..0 0..0 0..0 0..0
-512 0..0 11111110 1..1 1..1 1..1 1..1 1..1 1..1
Unlike the ordinal types (all integers, character, logical), the values of which are always matched with a number of integers and, therefore, are represented in the machine’s memory absolutely exactly, the value of real types determines the number only with some finite accuracy depending on the internal format of the real number .
Representation of real numbers in memory.
In some areas of computation, very large or very small real numbers are required. For greater accuracy, write floating point numbers are used. Writing a floating-point number is a very effective way of representing very large and very small real numbers, provided that they contain a limited number of significant digits, and, therefore, not all real numbers can be represented in memory. Usually the number of significant digits used in the calculations is such that for most problems rounding off errors are negligible.
The format for representing floating point numbers contains one or two fields of fixed length for characters. The number of positions for significant digits is different in different computers, but there is, nevertheless, a common format, shown in Figure 2.5 a). In accordance with this record, the format of a real number contains, in general, the fields of the mantissa, the order and the signs of the mantissa and the order.
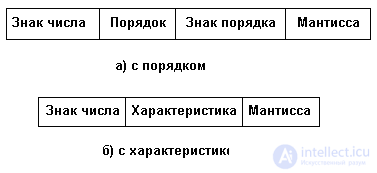
Fig. 2.5. The format of the representation of real numbers
However, more often, instead of the order, the characteristic is used, which is obtained by adding to the order of such an offset that the characteristic is always positive. In this case, there is a format for representing real numbers such as in Figure 2.5 b).
The introduction of characteristics eliminates the need to single out one bit for the order sign and simplifies the execution of comparison operations (<,>, <=,> =) and arithmetic operations on real numbers. So, when adding or subtracting floating-point numbers, in order to align the operands, the mantissa of the number must be shifted to the left or right. A shift can be made using a single counter, into which a positive number is first recorded, then decreasing until the required number of shifts is performed.
Thus, to represent real numbers in computer memory, the order p of a real number is represented as a characteristic by adding an offset (high order bit):
X = 2 ^ (n-1) + k + p, (2.1)
Where:
The formulas for calculating the characteristics and the number of bits required for its storage are given in Table 2.2.
| Type of | Harakteristika | The number of bits on Har-ku |
| real | x = 2 ^ 7 + p + 1 | eight |
| single | x = 2 ^ 7 + p - 1 | eight |
| double | x = 2 ^ 10 + p - 1 | eleven |
| extended | x = 2 ^ 14 + p - 1 | 15 |
Table 2.2
The next component of the floating-point number represented in the machine is the mantissa. In order to increase the number of significant digits in the representation of numbers and exclude overflow when multiplying, the mantissa is usually subjected to normalization. Normalization means that the mantissa (let's call it F), except for the case when F = 0, must be in the interval
R ^ (- 1) <= F <1.
For the binary number system R = 2. Then, due to the fact that 2 ^ (- 1) <= F <1, a nonzero mantissa of any stored floating point number must begin with a binary one. This is one of the advantages of the binary form of a floating-point number representation. Since the normalization process creates a fraction, the first bit of which is equal to 1, in the structure of some machines this unit is taken into account, but is not recorded in the mantissa. This unit is often called the hidden unit, and the resulting extra bit is used to increase the accuracy of the representation of numbers or their range.
The above normalization method is a classical method in which the result of the normalization is represented as a regular fraction, i.e. with one after a point and zero in the integer part of a number. But normalization of the mantissa can be done in different ways.
In the IBM PC, the normalized mantissa contains its most significant bit to the left of the point. In other words, the normalized mantissa in the IBM PC belongs to the interval 1 <= F <2. In the memory of the machine for real, single, double data, this bit is not stored, i.e. is "hidden" and is used to increase the order in single formats or to store a character in real format. For positive and negative numbers, the normalized mantissa in memory is represented in the direct code.
The first, most significant bit in the floating-point representation of numbers is a sign, and by convention, zero is a positive number and one is a negative number.
The number of bits to store the mantissa and the order depends on the type of real number. The total number of bytes, the ranges of valid values for the numbers of real types, as well as the number of significant digits after the decimal point in the representation of numbers are given in Table 2.3.
| Type of | Value range | Meaningful numbers | Size in bytes |
| real | 2.9 * 10 ^ (- 39) .. 1.7 * 10 ^ 38 | 11-12 | 6 |
| single | 1.4 * 10 ^ (- 45) .. 3.4 * 10 ^ 38 | 7-8 | four |
| double | 4.9 * 10 ^ (- 324) .. 1.8 * 10 ^ 308 | 15-16 | eight |
| extended | 3.1 * 10 ^ (- 4944) .. 1.2 * 10 ^ 4932 | 19-20 | ten |
Table 2.3
Algorithm of forming a machine representation of a real number in computer memory
The algorithm of formation consists of the following points:
Machine data representation type REAL
The format for machine representation of data of type REAL is as follows:
ml. byte art. byte
a: 7 0 15 8 23 16 31 24 39 32 47 40
x .... x m .... m m .... m m .... m m .... m sm ... m
b: 7 0 -32 -39 -24 -31 -16 -23 -8 -15 --1 -7
Where:
For example:
one). Decimal number 15.375;
in the binary number system 1111.011;
the result of the normalization is 1.111011 * 2 ^ 3; p = 3.
Considering the rejection of the implicit unit and the order shift, we get: s = 0; x = 2 ^ 7 + 1 + 3 = 2 ^ 7 + 2 ^ 2 = 132;
in the binary number system x = 10,000,100; m = 1110110 ... 0;
machine number representation:
10000100 00000000 00000000 00000000 00000000 01110110
2). Decimal number -0.5;
similar calculations give: normalized mantissa: 1.00 ... 0;
machine number representation:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
3). Decimal number -25.75;
similarly: the normalized mantissa: 1.10011100 ... 0;
machine number representation:
10000101 00000000 00000000 00000000 00000000 11001110
four). The number 0.0;
Machine number representation:
00000000 00000000 00000000 00000000 00000000 00000000
five). The numbers of the upper and lower bounds of the positive range
~ 1.7 * 10 ^ 38 -
11111111 11111111 11111111 11111111 11111111 01111111
~ 2.9 * 10 ^ (- 35) -
00000001 00000000 00000000 00000000 00000000 00000000
Machine data representation type SINGLE
The format for machine data representation of the SINGLE type is as follows:
ml. byte art. byte
7 0 15 8 23 22 16 31 30 24 - numbers of digits of memory
m .... m m .... m x m ... m s x ... x
-16 -23 -8 -15 0 -1 -7 7 1 - indicators of degrees of discharges
mantissas and characteristics
Where:
For example:
one). The number is -15.375;
in the binary notation -1111.011;
the normalized binary number is -1.111011 * 2 ^ 3; p = 3.
Given the rejection of the implicit unit and the order shift, we get: s = 1; x = 2 ^ 7-1 + 3 = 2 ^ 7 + 2 ^ 1 = 130;
in the binary number system x = 10000010; m = 1110110 ... 0;
machine representation of a number in the format of SINGLE:
00000000 00000000 01110110 11000001
2). The number is -0.1875;
in the binary number system -0.0011;
normalized binary number -1.1 * 2 ^ (- 3); p = -3.
Given the rejection of the implicit unit and the order shift, we get: s = 1; x = 2 ^ 7-1-3 = 2 ^ 7-2 ^ 2;
in the binary number system x = 01111100; m = 100 ... 0;
machine representation of a number in the format of SINGLE:
00000000 00000000 01000000 10111110
3). Decimal 4.5;
similar calculations give a normalized mantissa: 1.00100 ... 0;
machine number representation:
00000000 00000000 10010000 01000000
four). The values of the upper and lower bounds of the numbers of the negative range
~ -3.4 * 10 ^ 38 - 11111111 11111111 01111111 11111111 ~ -.4 * 10 ^ (- 45) - 00000001 00000000 00000000 10,000,000
DOUBLE machine data representation
The format for machine representation of data type DOUBLE is as follows:
ml of bytes st.byte 7 0 15 8 23 16 31 24 39 32 47 40 55 52 51 48 63 56 m ... m m ... m m ... m m ... m m ... m m ... m x..x m ... m s x..x -44 -50 -37 -43 -29 -36 -21 -28 -13 -20 -5 -12 3 0 -1 -4 10 4
Where:
For example:
one). The number is 15.375;
in the binary number system 1111.011;
the result of the normalization is 1.111011 * 2 ^ 3; p = 3.
Given the discarding of the hidden unit and the order shift, we get: s = 0; x = 2 ^ 10-1 + 3 = 2 ^ 10 + 2 ^ 1 = 1026;
in the binary number system x = 10000000010; m = 1110110 ... 0;
machine representation of a number in the DOUBLE format:
0 00000000 00000000 00000000 00000000 31
32 00000000 11000000 00101110 01000000 63
2). Decimal number 0.0375;
in binary number system 0.011;
normalization result 1.1 * 2 ^ (- 2); p = -2.
Given the discarding of the hidden unit and the order shift, we get: s = 0; x = 2 ^ 10-2 ^ 1-2 ^ 0 = 2 ^ 10-3;
in the binary number system x = 01111111101; m = 100 ... 0;
machine representation of a number in the DOUBLE format:
0 00000000 00000000 00000000 00000000 31
32 00000000 00000000 11011000 00111111 63
3). Decimal 2.5;
similar calculations give a normalized mantissa: 1.0100 ... 0;
machine representation of the number 2.5:
00000000 00000000 00000000 00000000
00000000 00000000 00000100 01000000
four). Values of the upper and lower limits of the range of positive numbers:
~ 1.8 * 10 ^ 308-11111111111111111111111111111111
11111111 11111111 11101111 01111111
~ 4.9 * 10 ^ (- 324) - 00000001 00000000 00000000 00000000
00000000 00000000 00000000 00000000
The symbol ~ denotes the approximate value of a number.
Machine representation of data type EXTENDED
The format for machine representation of data type EXTENDED is as follows:
ml of bytes art. byte 7 0 15 8 23 16 31 24 39 32 47 40 55 48 63 56 71 64 79 72 m..m m..m m..m m..m m..m m..m m..m m..m x..x sx..x -56-63-48-55-40-47-32-39-24-31-16-23-8 -15 0 -7 7 0 14 8
Where:
For example:
one). The number is -15.375;
in the binary notation -1111.011;
after normalization -1.111011 * 2 ^ 3; p = 3.
Given the presence of a hidden unit and an order shift, we get: s = 1; x = 2 ^ 14-1 + 3 = 2 ^ 14 + 2 ^ 1 = 16386;
in the binary number system x = 100000000000010; m = 11110110 ... 0
(in the mantissa, the unit to the left of the comma is not discarded).
The machine representation of this number in EXTENDED format:
0..0 0..0 0..0 0..0 0..0 0..0 0..0 11110110 00000010 11000000
2). The number 1.0;
similar calculations give
normalized mantissa: 1.0 ... 0;
machine representation of the number 1.0:
0..0 0..0 0..0 0..0 0..0 0..0 0..0 10000000 11111111 00111111
3). Values of the upper and lower limits of the range of positive numbers
(the * symbol denotes digits whose values for this characteristic are not identified, that is, their values do not affect the value of the mantissa):
~ 1.2 * 10 ^ 4932 - ******** ******** 11111111 11111111 11111111
11111111 11111111 11111111 11111111 011111111
~ 3.1 * 10 ^ 4944 - ******** ******** 00000001 00000000 000000000
00000000 00000000 00000000 00000001 000000000
2.1.3. Decimal types
Decimal types are not supported by PASCAL, but are available in some other languages, for example, COBOL, PL / 1. These types are used for the in-machine presentation of such data, which should first of all be stored in the computing system and provided to the user on demand, and only secondarily be processed (serve as operands of computational operations). It is no coincidence that these types first appeared in the COBOL language, which is focused on the processing of economic information: in most of the tasks in this sphere it is important to store and find information first, and its conversion is performed relatively rarely and comes down to the simplest arithmetic operations.
The architecture of some computing systems (for example, IBM System / 390) provides commands that work with a decimal representation of numbers, although these commands are much slower than binary arithmetic instructions. In other architectures, operations with decimal numbers are modeled programmatically.
Decimal types include: fixed-point decimal type and pattern type.
Fixed decimal type.
In PL / 1, the decimal type with a fixed point is described in the program as:
DECIMAL FIXED (md) or DECIMAL FIXED (m).
The first description means that the given is represented as a number consisting of m decimal digits, of which d digits are located after the decimal point. The second is an integer of m decimal digits. It should be emphasized that in any case the number of decimal digits in the number is fixed. The in-machine representation of integers and numbers with a fractional part is the same. For the latter, the position of the decimal point is remembered by the compiler and is taken into account by it when translating operations involving decimal numbers with a fixed point.
The in-machine representation of this type is called the decimal packed format. Examples of the representation of numbers in this format are shown in Fig. 2.6.
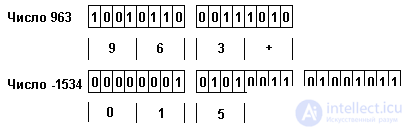
Fig.2.6. Machine representation of decimal numbers in packed format
Each decimal digit of a number occupies half a byte (4 binary digits) and is represented in this nibble by its binary code. Another half byte is occupied by the sign of the number, which is represented by the binary code 1010 - the sign "+" or 1011 - the sign "-". The representation occupies an integer number of bytes and, if necessary, is supplemented with a leading zero.
Template type.
In PL / 1, the pattern type is described in the program as: PICTURE '9 ... 9'.
This means that this is an integer containing as many digits as there are nines in the description.
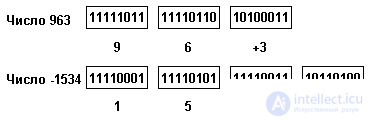
Fig.2.7. Machine representation of decimal numbers in zone format
The in-machine representation of this type, the so-called decimal zone format, is very close to such a representation of data that is convenient for the user: each decimal digit is represented by a byte: containing the character code of the corresponding digit. In IBM System / 390, which hardware supports the zone format, the EBCDIC character code is used, in which the character code of a digit contains the higher nibble code 1111, and the younger contains the binary code of the digit number. The sign is not included in the total number of digits in the number; for the representation of the sign in the highest nibble of the last digit of the number, the code 1111 is replaced by 1010 - the "+" sign or 1011 - the "-" sign.
Examples of the representation of numbers in the zone format are shown in Figure 2.7.
Above numeric types, as well as above all others, four main operations are possible first of all: creation, destruction, selection, updating. Specific operations on numeric types are well-known arithmetic operations: addition, subtraction, multiplication, division. The operation of exponentiation in some languages is also basic and is denoted by a special character or combination of characters (^ - in BASIC, ** - in PL / 1), in others - performed by built-in functions (pow in C).
Note that the division operation is performed differently for integers and real numbers. When dividing integers, the fractional part of the result is discarded, no matter how close to 1 it is. In this regard, in the PASCAL language there are even different designations for dividing real and integer numbers - the operations "/" and "div", respectively. In other languages, both types of division are denoted in the same way, and the type of division is determined by the type of operands. For whole operands, one more operation is possible - the remainder of the division - ("mod" - in PASCAL, "%" - in C).
Another group of operations on numeric types is the comparison operation: "equal", "not equal", "greater", "less", etc. It is significant that although the operands of these operations are data of numeric types, their result is a logical type - "true" or "false." Speaking about comparison operations, one should pay attention to the peculiarity of making comparisons for equality / inequality of real numbers. Since these numbers are represented in memory with some (not absolute) accuracy, their comparisons cannot always be completely reliable.
Since the same operations are valid for different numeric types, the problem of arithmetic expressions with type mixing arises. This creates some inconvenience for programmers, since in real problems expressions with mixed types are quite common. Therefore, most languages allow expressions whose operands are of different numeric types, but such expressions are processed in different languages in different ways. In PL / 1, for example, all the operands of an expression are reduced to one type — to the type of the variable in which the result will be written, and then the expression is evaluated. In the C language, type conversion is performed in the process of evaluating an expression, when performing each individual operation, without taking other operations into account; each operation is calculated with the precision of the most accurate operand involved. Programmer,using expressions with a mixture of types, must know exactly the rules for calculating them for the selected language.
Representation of bit types.
Some tasks may require working with individual binary bits of data. Most often such tasks arise in system programming, when, for example, a single discharge is associated with the state of a separate hardware switch or a separate data transfer bus, etc. Data of this type are represented as a set of bits packed in bytes or words and not related to each other. Operations on such data provide access to the selected bit of the given. In PASCAL, unsigned integer types byte and word perform the role of bit types. Above these types, in addition to operations characteristic of numeric types, bitwise operations are allowed. Similarly, the role of bit types is played by unsigned integers in C.
In PL / 1, there is a special data type - a string of bits declared in the program as: BIT (n).
Data of this type is a sequence of bits of length n. The string of bits occupies an integer number of bytes in memory and, if necessary, is padded with zeros on the right.
Operations on bit types.
Over bit types, three groups of specific operations are possible: Boolean algebra operations, shift operations, comparison operations.
Boolean algebra operations are NOT (not), OR (or), and (and), exclusive OR (xor). These operations are both in name and meaning similar to operations on logical operands, but the difference in their application to bit operands is that operations are performed on individual bits of operands.
So the operation is NOT that each bit of the operand changes the value to the opposite. Performing an operation, for example, OR on two bit operands, is that OR is executed between the first bit of the first operand and the first bit of the second operand; this gives the first bit of the result; then OR is executed between the second bit of the first operand and the second bit of the second, the second bit of the result is obtained, etc.
Below are examples of how to perform bitwise logical operations:
but).x = 01101100 c). x = 01101100
not x = 10010011 y = 11001110
x and y = 01001100
b).x = 01101100 g). x = 01101100
y = 11001110 y = 11001110
x or y = 11101110 x xor y = 10100010
In some languages (PASCAL), bitwise logical operations are designated in the same way as operations on logical operands and are recognized by the type of operands. In other languages (C), different designations are used for bitwise and general logical operations. Third (PL / 1) - bitwise operations are implemented by built-in functions of the language.
Shifts perform a binary code shift by a specified number of digits left or right. Of the three possible types of shift (arithmetic, logical, cyclic) in programming languages, only logical is usually implemented (for example, by the operations shr, shl in PASCAL).
In comparison operations, the bit data is interpreted as unsigned integers, and the comparison is performed as a comparison of integers. PL / 1 bit strings are a more general data type, to which the string data operations described in Chapter 4 also apply.
The boolean boolean values can be one of the previously declared constants false (false) or true (true).
Logical data occupies one byte of memory. In this case, the false value corresponds to the zero value of the byte, and the true value corresponds to any non-zero value of the byte. For example: false is always in the machine view: 00000000; true may look like this: 00000001 or 00010001 or 10,000,000.
However, it should be borne in mind that when performing the assignment of a logical type variable to the value true, the code 00000001 is always written in the corresponding memory field.
Over logical types, operations of Boolean algebra are possible - NOT (not), OR (or), AND (and), exclusive OR (xor) - the latter is implemented for a logical type not in all languages. In these operations, the operands of the logical type are considered as a whole - regardless of the bit composition of their internal representation.
In addition, it should be remembered that the results of a logical type are obtained by comparing data of any type.
Interestingly, in the C language, the data of the logical type is missing, their functions are performed by the data of numeric types, most often of the int type. In logical expressions, an operand of any numeric type that has a zero value is considered as "false", and a non-zero value - as "true." The logical type results are integers 0 (false) or 1 (true).
The value of the char character type is characters from some predefined set. In most modern personal computers, this set is ASCII (American Standard Code for Information Intechange). This set consists of 256 different characters arranged in a certain way and contains symbols of capital and small letters, numbers and other symbols, including special control characters. Some deviations from the ASCII standard are allowed, in particular, with appropriate system support, this set may contain letters of the Russian alphabet. Sequence numbers (coding) can be found in the relevant sections of technical descriptions.
The value of the char character type is 1 byte in memory. The code from 0 to 255 in this byte specifies one of the 256 possible ASCII table characters.
For example: the character "1" has ASCII code 49, therefore the machine representation will look like this: 00110001.
ASCII, however, is not possible. It is an expanded binary coded decimal interchange code (EBCDIC). In EBCDIC, the character code also has a different encoding than in ASCII.
Both ASCII and EBCDIC include only letters of the Latin alphabet. Symbols of national alphabets occupy "free places" in the tables of codes and, thus, one table can support only one national alphabet. This drawback is overcome in the multitude of UNICODE, which is becoming increasingly common primarily in UNIX-oriented systems. In UNICODE, each character is encoded in two bytes, which provides more than 64 thousand possible code combinations and makes it possible to have a single code table that includes all national alphabets. UNICODE is certainly promising, however, the ubiquitous transition to double-byte character codes may necessitate reworking a significant portion of existing software.
Specific operations on character types are only comparison operations. When comparing, character codes are treated as unsigned integers. Code tables are constructed in such a way that the results of the comparison obey the lexicographic rules: characters that take up spaces with lower numbers in the alphabet have smaller codes than characters that take up places with large numbers. Basically, the character data type is used as the base type for constructing the integrated type "character string", which is discussed in Chapter 4.
Logical structure
The enumerated type is an ordered data type defined by the programmer, i.e. the programmer lists all the values that a variable of this type can take. Values are non-repeating identifiers within the program, the number of which can not be more than 256, for example,
type color = (red, blue, green);
work_day = (mo, tu, we, th, fr);
winter_day = (december, january, february);
Machine view.
For an enumerable type variable, one byte is allocated to which the sequence number of the value assigned is written. The sequence number is determined from the type described, and the numbering starts from 0. Names from the enumeration type are constants, for example,
var B, C: color;
begin B: = blue; (* B = 1 *)
C: = green; (* C = 2 *)
Write (ord (B): 4, ord (C): 4); end.
After executing this fragment of the program, numbers 1 and 2 will be displayed on the screen. The contents of the memory for variables B and C are as follows:
B - 00000001; C - 00000010.
Operations
At the physical level above the variables of the enumerated type, the operations of creation, destruction, selection, updating are defined. In this case, the identification number of the identifier by its value and, conversely, by the identifier number of its value is performed.
At the logical level, variables of an enumerated type can only be used in Boolean type expressions and in comparison operations; this compares the serial numbers of values.
Logical structure
One of the ways to form new types from the existing ones is to limit the allowable range of values of some standard scalar type or a framework of the listed enumerated type. This limit is determined by setting the minimum and maximum range values. At the same time, the range of permissible values changes with respect to the base type, but the memory representation fully corresponds to the base type.
Machine view.
Interval type data can be stored depending on the upper and lower limits of the interval, regardless of the number of values included in this limit, as shown in Table 2.4. Interval type data requires one, two or four bytes of memory, for example,
var A: 220..250; (* Takes 1 byte *)
B: 2221..2226; (* Takes 2 bytes *)
C: 'A' .. 'K'; (* Takes 1 byte *)
begin A: = 240; C: = 'C'; B: = 2222; end.
After executing this program, the contents of the memory will be as follows:
A - 11,110,000; C - 01000011; B - 10101110 00001000.
Operations
At the physical level, above the interval type variables, the operations of creating, destroying, selecting, updating are defined. Additional operations are defined by the base type of the elements of the interval type.
| Base type | Maximum allowed range | Memory size required |
| Shortint | -128..127 | 1 byte |
| Integer | -32768..32767 | 2 bytes |
| Longint | -2147483648..2147483647 | 4 bytes |
| Byte | 0..255 | 1 byte |
| Word | 0..65535 | 2 bytes |
| Char | chr (ord (0)) .. chr (ord (255)) | 1 byte |
| Boolean | False..True | 1 byte |
Table 2.4
Note: the record chr (ord (0)) in the table should be understood as: a symbol with the code 0.
A) Interval type of character: the definition of the character code and, conversely, the character by its code.
Let a variable of type tz: 'd' .. 'h' be given. This variable is assigned the value 'e'. The memory byte allocated for this variable will store the ASCII code of the letter 'e', i.e. 01100101 (in the 10th submission 101).
B) Interval type from enumerated: determination of the ordinal number of the identifier by its value and, conversely, by the identifier number - its value.
At the logic level, all operations allowed for data of the base type are possible for the data of the corresponding interval types.
The type of pointer represents the address of the memory cell (in the overwhelming majority of modern computing systems the size of the cell — the minimum addressable unit of memory — is one byte). When programming at a low level — in machine codes, in Assembly language, and in C, which is specifically targeted at system programmers, work with addresses makes up a significant part of program codes. When solving applied problems using high-level languages, the most frequent cases where the programmer may need pointers are the following:
1) If you need to submit the same memory area, and therefore the same physical data as the data of different logical structures. In this case, the program introduces two or more pointers that contain the address of the same memory area, but have a different type (see below). Referring to this memory area with a pointer, the programmer treats its contents as data of one type or another.
2) When working with dynamic data structures, more importantly. Memory for such structures is allocated during program execution, standard memory allocation procedures / functions return the address of the allocated memory area - a pointer to it. The programmer can access the contents of the dynamically allocated memory area only through such a pointer.
The physical representation of the address essentially depends on the hardware architecture of the computing system. Consider as an example the address structure in the i8086 microprocessor.
The machine word of this processor has a size of 16 bits. If you use the address representation in one word, then you can address 64 KB of memory, which is clearly not enough for any serious software product. Therefore, the address is represented as two 16-bit words - a segment and offset. The segment part of the address is loaded into one of the special segment registers (in i8086 such registers 4). When addressing an address, the segment register identifier and a 16-bit offset are specified. The full physical (effective) address is obtained as follows. The segment of the address is shifted by 4 digits to the left, the digits freed from the left are filled with zeros, and the offset obtained in this way is added, as shown in fig. 2.8.
The resulting effective address has a size of 20 bits, so it allows you to address up to 1 MB of memory.
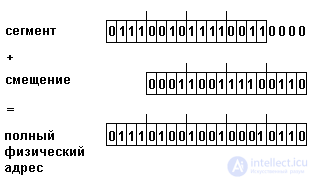
Figure 2.8. The calculation of the full address in the microprocessor i8086.
Once again, the physical structure of the address is fundamentally different for different hardware architectures. So, for example, in the i386 microprocessor, both components of the address are 32-bit; in the S / 390 family of processors, the address is represented as a 31-bit offset in one of the 19 address spaces; in the Power PC 620 processor, one 64-bit word can address all of the operational as well as external memory.
The MS DOS operating system was designed specifically for the i8086 processor and uses the described address structure even when executed on more advanced processors. However, today it is the only operating system in which the programmer can work with addresses in real memory and with the physical structure of the address. Without exception, all modern models of processors hardware perform the so-called dynamic address translation and, in conjunction with modern operating systems, ensure the operation of programs in virtual (apparent) memory. The program is developed and executed in some virtual memory, the addresses in which vary linearly from 0 to some maximum value. A virtual address is a number — a cell number in a virtual address space. The conversion of a virtual address into a real one is done by hardware every time a virtual address is accessed. This conversion is performed completely unnoticed (transparently) for the programmer, so in modern systems the programmer can consider the physical structure of an address a structure of a virtual address. The virtual address is an integer without a sign. In different computer systems, the bit depth of this number may vary. Most modern systems provide a 32-bit address that allows you to address up to 4 GB of memory, but there are already systems with 48 and even 64-bit addresses.
In a high-level language program, pointers can be typed and untyped. When a typed pointer is declared, the type of the object in the memory addressed by this pointer is determined. For example, ads in PASCAL:
Var ipt: ^ integer; cpt: ^ char;
or in C language:
int * ipt; char * cpt;
means that the ipt variable is the address of the memory area in which the integer is stored, and cpt is the address of the memory area in which the character is stored. Although the physical structure of the address does not depend on the type and value of the data stored at this address, the compiler considers the ipt and cpt pointers to have a different type, and in the Pascal statement:
cpt: = ipt;
will be interpreted by the compiler as erroneous (the C compiler for a similar assignment operator will be limited to a warning). Thus, when it comes to typed pointers, it is more correct to speak not of a single data type “pointer”, but of a whole family of types: “pointer to integer”, “pointer to character”, etc. There can be pointers to more complex, integrated data structures, and pointers to pointers.
An untyped pointer — the type of a pointer in Pascal or void * in C — is used to represent an address that contains data of unknown type. Working with untyped pointers is significantly limited, they can only be used to save the address, it is impossible to access the address specified by
продолжение следует...
Часть 1 2. SIMPLE DATA STRUCTURE
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.