Classification of sorting methods is rarely meaningful. Both of these methods that have been analyzed before can also be considered as "exchange" sortings. In this section, however, the method is described, where the exchange of places of the two elements is a characteristic feature of the process. The direct exchange algorithm outlined below is based on comparing and changing places for a pair of neighboring elements and continuing this process until all elements are ordered.
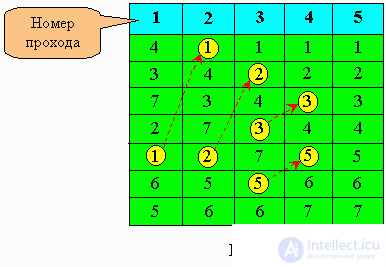
As in the direct selection method mentioned above, we repeat passes through the array, each time shifting the smallest element of the remaining sequence to the left end of the array. If we consider arrays as vertical rather than horizontal constructions, then the elements can be interpreted as bubbles in a tank of water, with the weight of each corresponding to its key. In this case, with each pass, one bubble as if rises to a level corresponding to its weight (see Figure 6.3).
This method is commonly known as bubble sorting. In its simplest form, it is presented below.
Pseudocode and Pascal programs:
for i = 2 to n
for j = n to i step -1
if a (j) <a (j - 1) then
x = a (j - 1)
a (j - 1) = a (j)
a (j) = x
endif
next j
next i
return |
for i: = 2 to n do
for j: = n downto i do
if a [j] <a [j - 1] then
begin
x: = a [j - 1];
a [j - 1]: = a [j];
a [j]: = x;
end;
end;
end; |
In our case, it turned out one pass “idle”. In order not to rearrange the elements once again, you can enter the
fl flag, which remains
false , if not a single exchange is made on the next pass. The following add algorithm is in italics.
fl = true for i = 2 to n
if fl = false then return endif fl = false for j = n to i step -1
if a (j) <a (j - 1) then
fl = true x = a (j - 1)
a (j - 1) = a (j)
a (j) = x
endif
next j
next i
return
The improvement of the bubble method is shaker sorting, where after each pass they change direction in the internal cycle.
Algorithm efficiency: The number of comparisons C
max = n (n-1) / 2, O (n
2 ).
The number of displacements M
max = 3C
max = 3n (n-1) / 2, O (n
2 ).
If the array is already sorted and an algorithm with a flag is applied, then just one pass is enough, and then we get the minimum number of comparisons
C
min = n - 1, O (n),
and there are no movements at all
A comparative analysis of direct sorts shows that the exchange "sort" in the classical form is a cross between sorts with the help of inclusions and with the help of choice. If the above improvements are made to it, then for reasonably ordered arrays, bubble sorting even has an advantage.

Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.