You get a bonus - 1 coin for daily activity. Now you have 1 coin

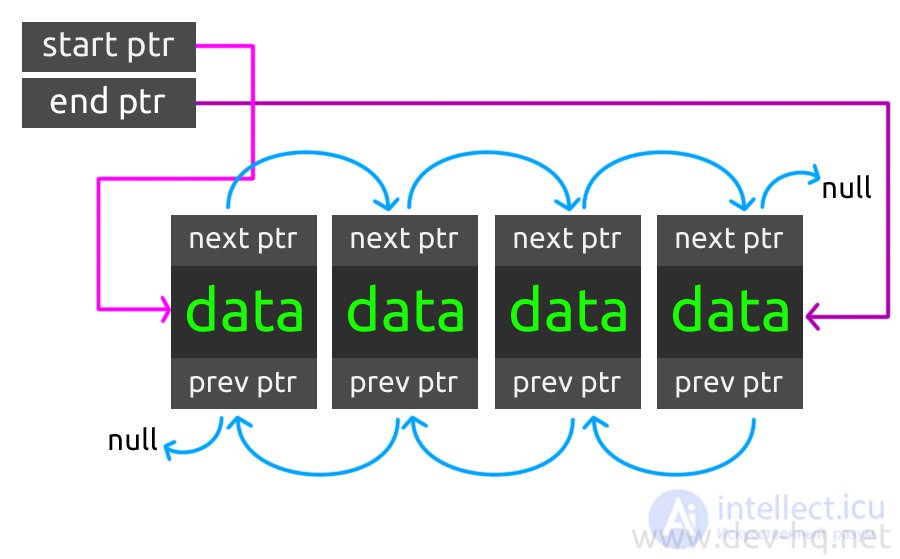
Doubly linked lists Animated examples. Comparing lists and arrays

Lecture



Doubly-connected linear lists

Unlike single-linked linear lists, doubly-connected, in addition to the data and next fields, have a prev field (a pointer to the previous list element):

Class of a doubly linked list node 

  type
   Node <T> = class
     data: T;
     prev, next: Node <T>;
 
     constructor (d: T; p, n: Node <T>);
     begin
       data: = d;
       prev: = p;
       next: = n;
     end;
   end;

In the case of a doubly linked list, it is enough for us to have a link to any node, then all the rest can be found. However, for convenience, we will assume that we have two links:

  • head - to the beginning of the list (start ptr)
  • tail - at the end of the list (end ptr)

Doubly linked lists Animated examples. Comparing lists and arrays 

  Delete the first list item
                                   
        + ------- + + ------- + + ------- +  
 \ / \ / \ -> | data |  | data |  | data |
        + --- + --- + + --- + --- + + --- + --- +
        |  0 |  | ---> |  |  | ---> |  |  0 |
        + --- + - A- + + - | - + - A- + + - | - + --- +
              | ________ |  | ________ |
 
                    turns into

        + ------- + + ------- + + ------- +
        | deleted |  \ / \ / \ -> | data |  | data |
        + --- + --- + + --- + --- + + --- + --- +
        |  0 |  0 |  |  0 |  | ---> |  |  0 |
        + --- + --- + + --- + - A- + + - | - + --- +
                               | ________ |

 Remove item from the middle of the list
 
        + ------- + + ------- + + ------- +  
 \ / \ / \ -> | data |  | data |  | data |
        + --- + --- + + --- + --- + + --- + --- +
        |  0 |  | ---> |  |  | ---> |  |  0 |
        + --- + - A- + + - | - + - A- + + - | - + --- +
              | ________ |  | ________ |
                   
                    turns into
                   ___________________
                  |  |
        + ------- + |  + ------- + + --- V --- +  
 \ / \ / \ -> | data |  |  | deleted |  | data |
        + --- + --- + |  + --- + --- + + --- + --- +
        |  0 |  | - '|  0 |  0 | ---> |  |  0 |
        + --- + - A- + + --- + --- + + - | - + --- +
              | _____________________ | 

 Delete the first list item
                                   
        + ------- + + ------- + + ------- +  
 \ / \ / \ -> | data |  | data |  | data |
        + --- + --- + + --- + --- + + --- + --- +
        |  0 |  | ---> |  |  | ---> |  |  0 |
        + --- + - A- + + - | - + - A- + + - | - + --- +
              | ________ |  | ________ |

                    turns into

        + ------- + + ------- + + ------- +  
 \ / \ / \ -> | data |  | data |  | deleted |
        + --- + --- + + --- + --- + + --- + --- +
        |  0 |  | ---> |  |  0 | ---> |  0 |  0 |
        + --- + - A- + + - | - + --- + + --- + --- +
              | ________ |

Fig. 22.7. Removing a doubly linked list item

Standard operations with doubly-connected linear lists

Comment. When performing any operation you need to monitor possible changes in the head and tail .

  • Initialization 
  head: = nil;
 tail: = nil;
  • Add item to top

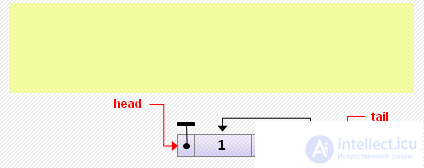
Doubly linked lists Animated examples. Comparing lists and arrays

Note. If the list was initially empty, after adding an element, you need to remember to make tail pointing to it. 

  head: = new Node <T> (0, nil, head);
 if head.next <> nil then
   head.next.prev: = head
 else // if the list was empty
   tail: = head;




  • Add item to end

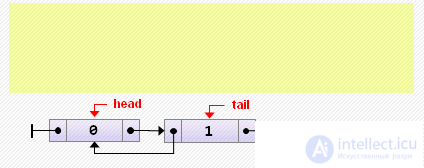
Doubly linked lists Animated examples. Comparing lists and arrays

Code  
  tail: = new Node <T> (2, tail, nil);
 if tail.prev <> nil then
   tail.prev.next: = tail
 else // if the list was empty
   head: = tail;



  • Remove item from start

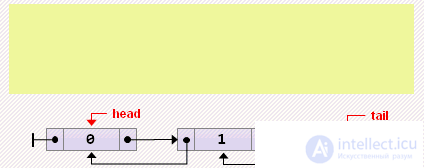
Doubly linked lists Animated examples. Comparing lists and arrays

Code  
  head: = head.next;
 if head = nil then
   tail: = nil
 else  
   head.prev: = nil;



  • Remove item from end

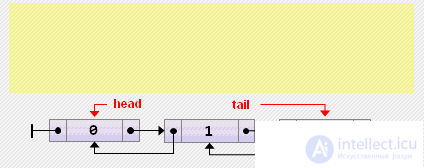
Doubly linked lists Animated examples. Comparing lists and arrays

Code  
  tail: = tail.prev;
 if tail = nil then
   head: = nil
 else
   tail.next: = nil;

  • Insert item before current

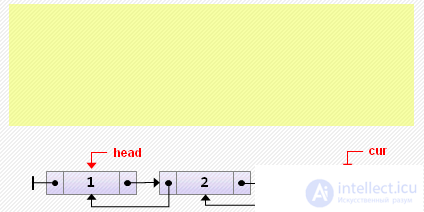
Doubly linked lists Animated examples. Comparing lists and arrays 

  if cur = head then
   // insert to the beginning
 else
 begin
   cur.prev: = new Node <T> (3, cur.prev, cur);
   cur.prev.prev.next: = cur.prev;
 end;

  • Insert item after current

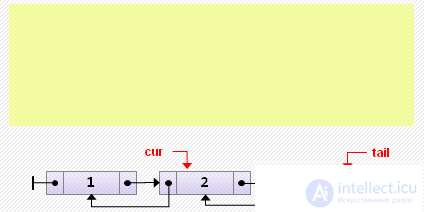
Doubly linked lists Animated examples. Comparing lists and arrays 

  if cur = tail then
   // insert at the end
 else
 begin
   cur.next: = new Node <T> (3, cur, cur.next);
   cur.next.next.prev: = cur.next;
 end;

  • Delete current

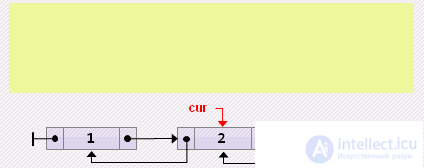
Doubly linked lists Animated examples. Comparing lists and arrays

Code 
  if cur = head then
   // remove from start
 else if cur = tail then
   // delete from end
 else
 begin
   cur.prev.next: = cur.next;
   cur.next.prev: = cur.prev;
   cur: = cur.next;
 end;

An example .
Given a doubly connected linear list with integer values.
Remove all its negative elements. 

  var list: DoublyLinkedList <integer>;
 // create a list
 
 var cur: = list.head;
 while cur <> nil do
   if cur.data <0 then
     cur: = list.RemoveAt (cur)
   else
     cur: = cur.next;


Create a class of doubly connected linear list whose fields are head and tail : 

  type
   Node <T> = class
     data: T;
     prev, next: Node <T>;
 
     constructor (d: T; p, n: Node <T>);
     begin
       data: = d;
       prev: = p;
       next: = n;
     end;
   end;
 
   DoubleLinkedList <T> = class
     head, tail: Node <T>;
 
     constructor;
     begin
       head: = nil;
       tail: = nil;
     end;
 
     procedure AddFirst (d: T);
     begin
       head: = new Node <T> (d, nil, head);
       if head.next <> nil then
         head.next.prev: = head
       else // if the list was empty
         tail: = head;
     end;
     procedure AddLast (d: T);
     begin
       tail: = new Node <T> (d, tail, nil);
       if tail.prev <> nil then
         tail.prev.next: = tail
       else // if the list was empty
         head: = tail;
     end;
 
     procedure DeleteFirst;
     begin
       head: = head.next;
       if head = nil then
         tail: = nil
       else  
         head.prev: = nil;
     end;
     procedure DeleteLast;
     begin
       tail: = tail.prev;
       if tail = nil then
         head: = nil
       else
         tail.next: = nil;
     end;
 
     procedure InsertBefore (cur: Node <T>; d: T);
     begin
       if cur = head then
         AddFirst (d)
       else
       begin
         cur.prev: = new Node <T> (d, cur.prev, cur);
         cur.prev.prev.next: = cur.prev;
       end;
     end;
     procedure InsertAfter (cur: Node <T>; d: T);
     begin
       if cur = tail then
         AddLast (d)  
       else
       begin
         cur.next: = new Node <T> (d, cur, cur.next);
         cur.next.next.prev: = cur.next;
       end;
     end;
 
     function RemoveAt (cur: Node <T>): Node <T>;
     begin
       if cur = head then
         begin
           DeleteFirst;
           Result: = head;
         end       
       else if cur = tail then
         begin
           DeleteLast;
           Result: = nil;
         end
       else if cur = tail then
       begin
         DeleteLast;
         result: = nil;
       end
       else
       begin
         cur.prev.next: = cur.next;
         cur.next.prev: = cur.prev;
         result: = cur.next;
       end;
     end;
 
     procedure Print;
     begin
       var cur: = head;
       while cur <> nil do
       begin
         writeln (cur.data);
         cur: = cur.next;
       end;
     end;
     procedure PrintReverse;
     begin
       var cur: = tail;
       while cur <> nil do
       begin
         writeln (cur.data);
         cur: = cur.prev;
       end;
     end;
   end;

Comparing lists and arrays

the number of operation (n - the number of elements)

Array List
Insert at end, delete from end 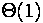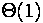Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays
Insert at the beginning, delete from the beginning 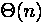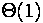Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays
Insert in the middle, removal from the middle 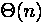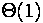Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays
Pass 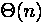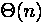Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays
Access by index 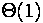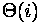Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays
Search 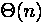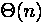Doubly linked lists Animated examples. Comparing lists and arrays Doubly linked lists Animated examples. Comparing lists and arrays

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Structures and data processing algorithms.

Terms: Structures and data processing algorithms.