Lecture
Consider the algorithm for inserting a node into a binary tree.
Insert the node with the number 150, then it will become the right son of the node with the number 120, since it is large in value of node number 120, but less than the value of node in the head of the tree.
P - working pointer
Q - pointer lagging behind P by one step
V is a pointer to the element that will be inserted into the binary tree. 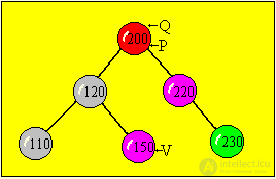
Illustration of the process of inserting a node 150, in accordance with the above algorithm (in red, new links in the tree are highlighted). 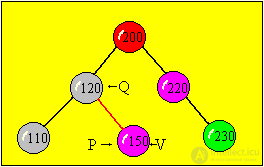
The final version of the tree after insertion: 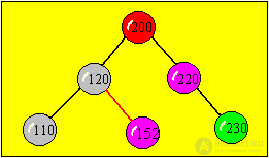
Program
Pseudocode pascal
Q = nil Q = nil
P = Tree P = Tree
While (P <> nil) do While (P <> nil) do
Q = P Begin
If key = k (P) then Q = P;
search = If key = P ^ .k then
return begin
EndIf search: = P;
If key <k (p) then = "" exit; <br = "">
P = left (P) End;
else if key
P = right (P) P: = P ^ .left;
Endif else
EndWhile P: = P ^ .right;
V = maketree (key, rec) End;
If key <k (q) then = "" v = "maketree (key, rec) <br">
else If key <q ^ .k then <br = "">
Right (Q) = VQ ^ .left: = V
Endif else
search = VQ ^ .right: = V;
Return search: = V
Using a random number generator to form a binary tree consisting of 5 elements (provide manual input of elements). Moreover, the numbers should be in the range from -99 to 99. Perform a search with the insertion of elements in accordance with the following options for tasks:
1. The numbers are multiples of N.
2. Odd numbers.
3. Numbers> N.
4. Prime numbers.
5. Numbers to choose from.
6. Random number.
7. Compound numbers.
8. Numbers from X to Y.
9. Numbers whose sum of digits (by module) is> N.
10. Numbers whose sum of numbers (by module) is <N.
11. Numbers, the sum of the digits (modulo) of which lies in the interval from X to Y.
12. Numbers, taken in absolute value, the square root of which is an integer.
where: N, X, Y - is set by the teacher.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.