5.6 Binary search (halving method)
We will assume that we have an array of numbers ordered in ascending order. The main idea is to randomly select some element
AM and compare it with the search argument X. If A
M = X, then the search is completed; if A
M M> X.
The choice of M is completely arbitrary in the sense that the correctness of the algorithm does not depend on it. However, the choice affects its effectiveness. It is clear that our task is to exclude as many elements as possible from the further search. The best solution is to choose the middle element, i.e. middle of the array.
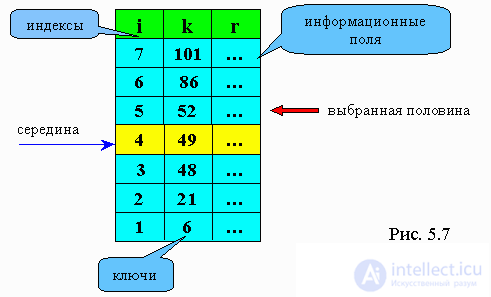
Consider the example shown in Fig. 5.7. Suppose we need to find an element with a key 52. The first element to be compared is 49. Since 49 <52, we are looking for the next middle among the elements located above 49. This number is 86. 86> 52, therefore we are now looking for 52 among the elements located below 86 , but above 49. In the next step, we find that the next value of the middle is equal to 52. We found an element in the array with the specified key.
Pseudocode and Pascal programs:
Low = 1
hi = n
while (low <= hi) do
mid = (low + hi) div 2
if key = k (mid) then
search = mid
return
endif
if key
hi = mid - 1
else low = mid + 1
endif
endwhile
search = 0
return |
low: = 1;
hi: = n;
while (low <= hi) do
begin
mid: = (low + hi) div 2;
if key = k [mid] then
begin
search: = mid;
exit;
end;
if key
then hi: = mid - 1
else low: = mid + 1;
end;
search: = 0;
exit |
If key = 101, the record will be found in three comparisons (in a sequential search, seven comparisons would be needed).
If
C is the number of comparisons, and
n is the number of elements in the table, then
C = log 2 n.
For example,
n =
1024 .
With sequential search
C = 512 , and with binary
C =
10 .
You can combine binary and index-sequential search (for large amounts of data), given that the latter is also used when sorted array.
5.7. Search in binary tree
Its purpose is to search for a node of the tree according to a given key. The duration of the operation depends on the structure of the tree. Indeed, a tree can be degenerate into a unidirectional list, like the right one in fig. 5.8.
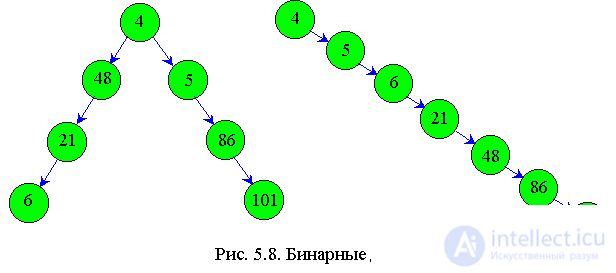
In this case, the search time will be the same as in the unidirectional list, i.e. will have to sort through N / 2 items.
The greatest effect of using the tree is achieved in the case when the tree is balanced. In this case, no more than
log 2 N elements should be searched for.
A strictly balanced tree is a tree in which each node has left and right subtrees differing in level by no more than one.
The search for an element in a binary tree is called a binary search in a tree.
Such a tree is called a binary search tree.
The essence of the search is as follows. Analyze the top of the next subtree. If the key is less than the vertex information field, then we analyze the left subtree, more - the right one.
Let the key argument be given
p = tree
whlie p <> nil do
if key = k (p) then
search = p
return
endif
if key
p = left (p)
else
p = right (p)
endif
endwhile
search = nil
return |
p: = tree;
whlie p <> nil do
begin
if key = p ^ .k then
begin
search: = p;
exit;
end;
if key
p: = p ^ .left
else
p: = p ^ .right;
end;
search: = nil;
|


Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.