6.4.1. Quick Sort
Refers to exchange sorting methods. The basis is the method of separation of keys in relation to the selected.
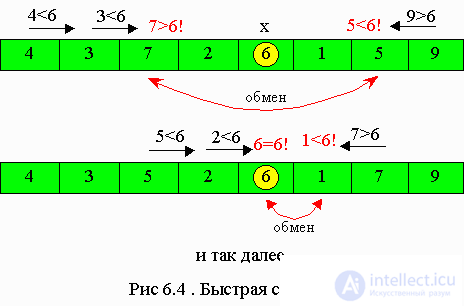
To the left of 6, all keys with smaller keys are located, and to the right, with greater or equal to 6 (Fig. 6.4).
Sub Sort (L, R)
i = L
j = r
x = a ((L + R) div 2)
repeat
while a (i) <x do
i = i + 1
endwhile
while a (j)> x do
j = j - 1
endwhile
if i <= j then
y = a (i)
a (i) = a (j)
a (j) = y
i = i + 1
j = j - 1
endif
until i> j
if L <j then
sort (L, j)
endif
if i <R then
sort (i, R)
endif
return
sub QuickSort
sort (1, n)
return |
procedure Sort (L, R: integer);
begin
i: = L;
j: = r;
x: = a [(L + r) div 2];
repeat
while a [i] <x do
i: = i + 1;
while a [j]> x do
j: = j - 1;
if i <= j then
begin
y: = a [i];
a [i]: = a [j];
a [j]: = y;
i: = i + 1;
j: = j - 1
end;
until i> j;
if L <j then sort (L, j);
if i <r then sort (i, r);
end;
procedure QuickSort ;
begin
sort (1, n);
end;
|
Algorithm efficiency: O (n log n) is the most efficient method.
6.4.2 Shell sorting (sorting in decreasing steps)
In 1959, D. Shell proposed the improvement of sorting using the live inclusion method. His work is presented in Fig. 6.5:

First, the elements that are separated from each other at a distance of 4 are separately grouped and sorted. This process is called quadruple sorting. After the first pass, the elements are regrouped - now each element of the group is 2 positions apart from the other - and re-sorted. This is called double sorting. And, finally, on the third pass is a normal or single sort.
At first glance, one can begin to doubt: if several sorting processes are necessary, and all the elements are included in each, will they add more work than they save? However, at each stage, relatively few elements are sorted, or the elements are already fairly well ordered and require relatively few permutations.
It is clear that such a method results in an ordered array, and, of course, it is immediately obvious that each pass only gains from the previous ones; it is also obvious that the distances in groups can be reduced in different ways, if only the latter is single, because in the worst case, the last pass will do all the work.
The given algorithm is based on the direct insertion method without a barrier and is not focused on a certain specific sequence of distances, although steps 5, 3 and 1 are specified for concreteness.
When using the barrier method, each of the sorts needs to set up its own barrier, and the program for determining its location should be made as simple as possible. Therefore, we have to expand the array to [-h1..N].
h [1..t] - array of step sizes
a [1..n] is a sortable array
k - sorting step
x - the value of the inserted element
Subroutine ShellSort
Pseudocode:
const t = 3
h (1) = 5
h (2) = 3
h (3) = 1
for m = 1 to t
k = h (m)
for i = k + 1 to n
x = a (i)
for j = i - k to 1 step -k
if x <a (j) then
a (j + k) = a (j)
else
goto L
endif
next j
L: a (j + k) = x
next i
next m
return
|
Pascal:
const t = 3;
h (1) = 5;
h (2) = 3;
h (3) = 1;
var
h: array [1..t] of integer;
a: array [1..n] of integer;
k, x, m, t, i, j: integer;
begin
for m = 1 to t do
begin
k: = h (m);
for i = k + 1 to n do
begin
x: = a (i);
for j = ik downto k do
begin
if x <a (j) then
a (j + k): = a (j);
else
goto 1;
end;
end;
end;
1: a (j + 1) = x;
end;
end. |
It is not proved which distances give the best result, but they should not be multipliers of each other.
D. Knut suggests the following sequence of steps (in reverse order): 1, 3, 7, 15, 31, ... That is: h
m -1 = h
m + 1,
t = log
2 n - 1. With such an organization of the algorithm, its efficiency is of the order
O (n
1. 2 )
test questions
What is sorting?
What are the main methods of sorting.
What sorting methods are strict?
What sorting methods are improved?
What sorting is called sustainable?
What is the essence of the method of direct inclusion?
What is the essence of the method of direct selection?
What is the essence of the method of direct exchange?
What is the difference between these three methods?
What sorting method is the most efficient?
Which of the main methods is the Shell method?


Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.