Lecture
One of the most interesting programming tasks is the implementation of sparse arrays. A sparse array , or a sparse array (sparse array), is an array in which not all elements are used, available or needed at the moment. Sparse arrays are useful in cases where two conditions are met: the size of the array that is required by the application is large enough (perhaps more than the amount of available memory), and when not all elements of the array are used. Thus, a sparse array is usually a large, but rarely full array. As will be shown later, there are several ways to implement sparse arrays. But before proceeding to their consideration, let's pay attention to the problems that are solved using sparse arrays.

To understand why sparse arrays are needed, recall the following two facts:
The fact that the memory for an array is allocated when it is created means that the size of the largest array that you can describe in your program is limited (in particular) by the amount of available memory. If you need a larger array than the capacity of the computer allows, you will have to implement it in some other way. (For example, one or another form of virtual memory is usually used to work with completely filled large arrays.) Even if a large array is located in memory, creating it can significantly reduce the available system resources, since the memory occupied by a large array is inaccessible to the rest of the program. and other processes running on the system. And this, in turn, may adversely affect the overall performance of the program or computer as a whole. In situations where not all elements of an array will be used, allocating memory for the entire array seems to be a particularly wasteful waste of system resources.
To get rid of the problems caused by the need for memory for large, rarely filled arrays, some techniques for working with sparse arrays were invented. All of them are characterized by one common feature: memory for array elements is allocated only when necessary. Therefore, the advantage of a sparse array is that it only requires as much memory as is needed to store only those elements that are actually used. In this case, the remaining memory can be used for other purposes. In addition, these techniques allow you to create very large arrays, the size of which is much larger than the size allowed by the system of ordinary arrays.
There are numerous examples of applications that require processing sparse arrays. Many of them are related to working with matrices or to scientific and engineering problems that are understandable only to experts in relevant fields. However, there is one very popular application in which a sparse array is usually used - a spreadsheet. Despite the fact that the matrix in the average spreadsheet is very large, at any given time only some of it is used. Formulas, values, and strings are stored in spreadsheet cells. When using a sparse array, memory for each element is allocated only when necessary. Since only a small part of the elements of the array are actually used, the whole of it (that is, the spreadsheet) seems very large, but it takes up the minimum necessary memory.
In this chapter, two terms will often be repeated: the logical array and the physical array . A logical array is an array that is thought of as existing in the system. For example, if a spreadsheet matrix has a size of 1`000x1`000, then a logical array that implements the matrix will also have a size of 1`000x1`000 - even though physically such an array does not exist in the computer. A physical array is an array that actually exists in computer memory. So, if only 100 elements of the spreadsheet matrix are used, then the memory required to store only these 100 elements is required to store the physical array. Sparse array processing methods, disclosed in this chapter, provide a link between logical and physical arrays.
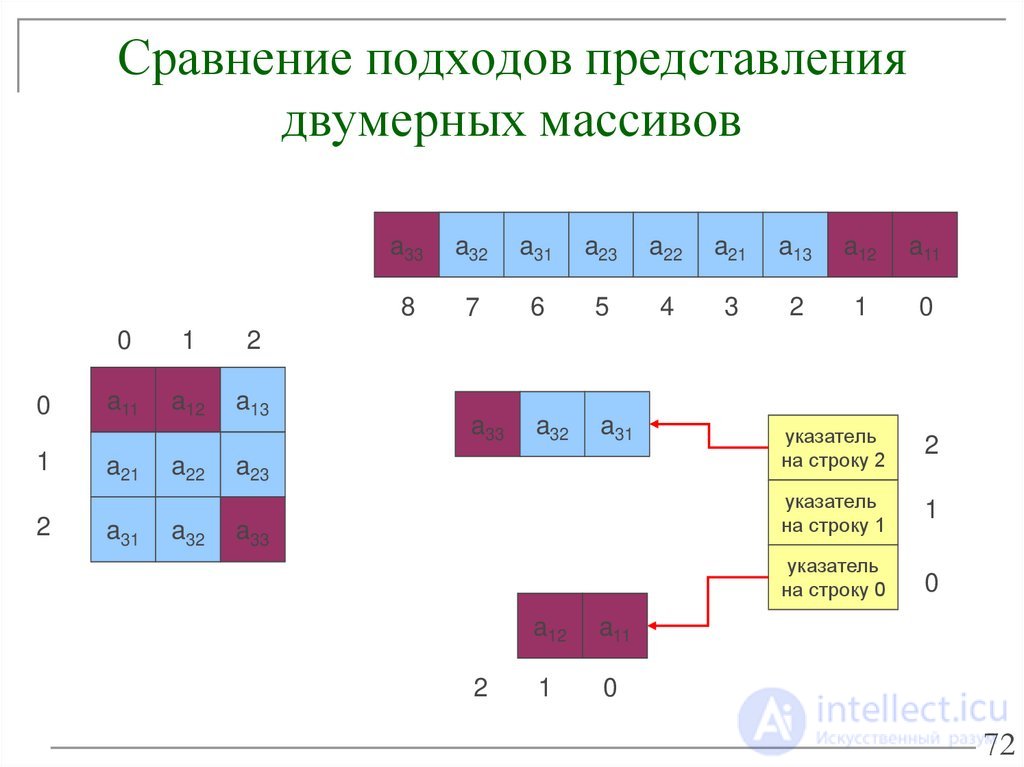
Below are four different ways to create a sparse array: a linked list, a binary tree, an array of pointers, and hashing. Although the spreadsheet program is not fully developed, all examples focus on the spreadsheet matrix shown in Figure 2. 23.1. In this figure, element X is located in cell B2.
Fig. 23.1. Simple Spreadsheet Organization
--- A --- --- B --- --- C --- one 2 X 3 four five 6 7 . . Fig. 23.1. Simple Spreadsheet Organization |
When implementing a sparse array using a linked list, the first step is to create a structure containing the following elements:
Each new structure is placed in the list so that the elements remain ordered by index in the array. Access to the array is made by clicking on the links.
For example, the following structure can be used as a carrier of a sparse array element in a spreadsheet:
struct cell {
char cell_name [9]; / * cell name, eg A1, B34 * /
char formula [128]; / * information, for example, 10 / B2 * /
struct cell * next; / * pointer to the next entry * /
struct cell * prior; / * pointer to the previous entry * /
};
The cell_name field contains the string corresponding to the cell name, for example, A1, B34 or Z19. The string field formula stores the formula (data) from the corresponding table cell.
A complete spreadsheet program would be too large [1] to use as an example. Instead, this chapter discusses key functions that provide sparse array implementation based on a linked list. It should be remembered that there are many ways to implement a spreadsheet program. The functions and data structure shown here are just examples of working with sparse arrays.
The following global variables indicate the beginning and end of a linked list:
struct cell * start = NULL; / * first list item * / struct cell * last = NULL; / * last list item * /
In most spreadsheets, when a formula is entered into a cell, a new element of a sparse array is created. If the spreadsheet is based on a linked list, this element is inserted into the list using a function similar to the dls_store () function in Chapter 22. Remember that the list is sorted by cell name; for example, A12 precedes A13, etc.
/ * Insert cells into an ordered list. * /
void dls_store (struct cell * i, / * pointer to the inserted cell * /
struct cell ** start,
struct cell ** last)
{
struct cell * old, * p;
if (! * last) {/ * first item in the list * /
i-> next = NULL;
i-> prior = NULL;
* last = i;
* start = i;
return;
}
p = * start; / * start at the top of the list * /
old = NULL;
while (p) {
if (strcmp (p-> cell_name, i-> cell_name) <0) {
old = p;
p = p-> next;
}
else {
if (p-> prior) {/ * is an element from the middle * /
p-> prior-> next = i;
i-> next = p;
i-> prior = p-> prior;
p-> prior = i;
return;
}
i-> next = p; / * new first item * /
i-> prior = NULL;
p-> prior = i;
* start = i;
return;
}
}
old-> next = i; / * insert at the end * /
i-> next = NULL;
i-> prior = old;
* last = i;
return;
}
In the above function, the parameter i is a pointer to a new inserted cell. The parameters start and last are respectively pointers to pointers to the beginning and end of the list.
The following deletecell () function deletes a cell from the list whose name is passed as a parameter.
void deletecell (char * cell_name,
struct cell ** start,
struct cell ** last)
{
struct cell * info;
info = find (cell_name, * start);
if (info) {
if (* start == info) {
* start = info-> next;
if (* start) (* start) -> prior = NULL;
else * last = NULL;
}
else {
if (info-> prior) info-> prior-> next = info-> next;
if (info! = * last)
info-> next-> prior = info-> prior;
else
* last = info-> prior;
}
free (info); / * free up system memory * /
}
}
The last function you need to implement a sparse array based on a linked list is the find () function that finds the specified cell. To find a cell of this function, you have to perform a linear search, but, as shown in Chapter 21, the average number of comparisons in a linear search is n / 2, where n is the number of items in the list. The following is the text of the find () function:
struct cell * find (char * cell_name, struct cell * start)
{
struct cell * info;
info = start;
while (info) {
if (! strcmp (cell_name, info-> cell_name)) return info;
info = info-> next; / * go to the next cell * /
}
printf ("Cell not found. \ n");
return NULL; / * search failed * /
}
The principal advantage of the method of implementing a sparse array using a linked list is that it allows efficient use of memory - space is allocated only for those elements of the array that actually contain information. In addition, it is easy to implement. However, this method has one major drawback: it uses linear search to access cells. Moreover, the cell saving procedure also uses a linear search to find the place to insert a new item. These problems can be solved by building a sparse array based on a binary tree, as shown below.
[1] Many users joke that Microsoft itself does not know how much Excel it exactly takes. Of course, this is only a joke, but personally I sometimes think that it is 100% true.

In essence, a binary tree is simply a modified doubly linked list. Its main advantage is the ability to quickly search. Due to this, it is possible to very quickly perform inserts and spend quite a bit of time on access to the elements. (After all, binary trees are ideal for applications that require a linked list structure in which the search should take very little time.)
To use a binary tree to implement a spreadsheet, you need to change the cell structure as follows:
struct cell {
char cell_name [9]; / * cell name, eg A1, B34 * /
char formula [128]; / * data, eg, 10 / B2 * /
struct cell * left; / * pointer to the left subtree * /
struct cell * right; / * pointer to the right subtree * /
} list_entry;
The street () function in Chapter 22 can be modified to build a tree based on the cell name. The following code assumes that the parameter n is a pointer to an inserted tree element.
struct cell * stree (
struct cell * root,
struct cell * r,
struct cell * n)
{
if (! r) {/ * first vertex of the subtree * /
n-> left = NULL;
n-> right = NULL;
if (! root) return n; / * first entrance to the tree * /
if (strcmp (n-> cell_name, root-> cell_name) <0)
root-> left = n;
else
root-> right = n;
return n;
}
if (strcmp (r-> cell_name, n-> cell_name) <= 0)
stree (r, r-> right, n);
else
stree (r, r-> left, n);
return root;
}
When calling the stree () function, it needs to pass pointers to the root of the tree as the first two parameters and a pointer to the new cell as the third. The function returns a pointer to the root.
To delete a cell of a spreadsheet, you can use the modified dtree () function shown below, which takes the cell name as a key:
struct cell * dtree (
struct cell * root,
char * key)
{
struct cell * p, * p2;
if (! root) return root; / * item not found * /
if (! strcmp (root-> cell_name, key)) {/ * root removal * /
/ * it means an empty tree * /
if (root-> left == root-> right) {
free (root);
return NULL;
}
/ * or if one of the subtrees is empty * /
else if (root-> left == NULL) {
p = root-> right;
free (root);
return p;
}
else if (root-> right == NULL) {
p = root-> left;
free (root);
return p;
}
/ * or if both subtrees are non-empty * /
else {
p2 = root-> right;
p = root-> right;
while (p-> left) p = p-> left;
p-> left = root-> left;
free (root);
return p2;
}
}
if (strcmp (root-> cell_name, key) <= 0)
root-> right = dtree (root-> right, key);
else root-> left = dtree (root-> left, key);
return root;
}
Finally, to quickly find a cell in a spreadsheet by its name, you can use a modified version of the search () function.
struct cell * search_tree (
struct cell * root,
char * key)
{
if (! root) return root; / * empty tree * /
while (strcmp (root-> cell_name, key)) {
if (strcmp (root-> cell_name, key) <= 0)
root = root-> right;
else root = root-> left;
if (root == NULL) break;
}
return root;
}
Using a binary tree significantly reduces the time to insert and search for items compared to a linked list. It should be remembered that sequential search requires on average n / 2 comparisons, where n is the number of list items. Compared to this, a binary search requires only log 2 n comparisons (if the tree is balanced). In addition, binary trees also use memory as economically as linked lists. However, in some situations there are better alternatives than binary trees.
Suppose that a spreadsheet has a size of 26x100 (from A1 to Z100), that is, it consists of 2'600 elements. Theoretically, table elements can be stored in the following array of structures:
struct cell {
char cell_name [9];
char formula [128];
} list_entry [2600]; / * 2600 cells * /
Ho 2`600 multiplied by 137 bytes (the size of this structure in bytes) is 356`200 bytes of memory. This is too much memory to waste on an incompletely used array. Nevertheless, it is possible to create an array of pointers (pointer array) on structures of the type cell . It takes much less memory to store an array of pointers than an array of structures. Each time a cell is assigned a logical data array, memory is allocated for this data, and the address of the selection is assigned to the corresponding pointer in the array of pointers. This scheme allows to achieve higher performance than with a linked list or binary tree. The description of the array of pointers is as follows:
struct cell {
char cell_name [9];
char formula [128];
} list_entry;
struct cell * sheet [2600]; / * array of 2600 pointers * /
This smaller memory array is used to store pointers to the data entered in the spreadsheet. When you enter the next entry in the appropriate cell of the array is entered a pointer to the entered data. In fig. Figure 23.2 shows what a sparse array looks like in memory, represented as an array of pointers.
Fig. 23.2. Representation of a sparse array as an array of pointers
+ - + - + - + - + - + - + - + - + - + - + - + - +
|. |. | 0 | 0 |. | 0 | 0 | 0 |. | 0 | 0 | 0 |
+ | + | + - + - + | + - + - + - + | + - + - + - +
| | | | + ---- +
| | | '-> | A [8] |
| | | + ---- +
| | | + ---- +
| | '-> | A [4] |
| | + ---- +
| | + ---- +
| '-> | A [1] |
| + ---- +
| + ---- +
'-> | A [0] |
+ ---- +
|
Before using an array of pointers, each of its elements must be initialized to zero ( NULL ), which means the absence of this entry. The following is the array initialization function:
void init_sheet (void)
{
register int t;
for (t = 0; t <2600; ++ t) sheet [t] = NULL;
}
When a user enters a formula in a cell that occupies a certain position in the spreadsheet (and the position of the cell, as is known, is determined by its name), the index is calculated in the array of pointers sheet . This index is obtained by converting the string representation of the cell name into a number, as shown in the following listing:
void store (struct cell * i)
{
int loc;
char * p;
/ * calculate the index by the given name * /
loc = * (i-> cell_name) - 'A'; / * column * /
p = & (i-> cell_name [1]);
loc + = (atoi (p) -1) * 26; / * number of lines * line width +
column * /
if (loc> = 2600) {
printf ("Cell outside the array. \ n");
return;
}
sheet [loc] = i; / * put pointer into array * /
}
When calculating the index in the store () function, it is assumed that all cell names begin with a capital letter followed by an integer, for example, B34, C19, etc. Therefore, as a result of calculations using the formula programmed in the store () function, the cell name A1 corresponds to index 0, the name B1 corresponds to index 1, A2 - 26, and so on. Since the cell names are unique, the indices are also unique and the pointer to each record is stored in the corresponding array position. If you compare this procedure with versions using a linked list or binary tree, it becomes clear how much simpler and shorter it is.
The deletecell () cell deletion function also becomes very short. When called, it simply resets the pointer to the element and returns the system memory.
void deletecell (struct cell * i)
{
int loc;
char * p;
/ * calculation of the index for a given cell name * /
loc = * (i-> cell_name) - 'A'; / * column * /
p = & (i-> cell_name [1]);
loc + = (atoi (p) -1) * 26; / * number of lines * line width +
column * /
if (loc> = 2600) {
printf ("Cell outside the array. \ n");
return;
}
if (! sheet [loc]) return; / * do not free if pointer is zero
(null) * /
free (sheet [loc]); / * free up system memory * /
sheet [loc] = NULL;
}
This code is also much faster and easier than with the linked list version.
The process of finding a cell by name is simple, since the cell name uniquely identifies the index in the array of pointers. Therefore, the search function takes the following form:
struct cell * find (char * cell_name)
{
int loc;
char * p;
/ * calculation of the index for a given cell name * /
loc = * (cell_name) - 'A'; / * column * /
p = & (cell_name [1]);
loc + = (atoi (p) -1) * 26; / * number of lines * line width +
column * /
if (loc> = 2600 ||! sheet [loc]) {/ * this cell is empty * /
printf ("Cell not found. \ n");
return NULL; / * search unsuccessful * /
}
else return sheet [loc];
}
The sparse array implementation method based on an array of pointers provides much faster access to elements than methods based on a linked list and binary tree. If the array is not very large, allocating memory for the array of pointers only slightly reduces the amount of free system memory. However, in the array of pointers, a certain amount of memory is allocated for each cell, regardless of whether it is used or not. In some applications this may be a limitation, although in general this is not a problem.
Hashing (hashing) is the process of obtaining the index of an element of an array directly as a result of operations performed on a key that is stored with the element or even coincides with it. The generated index is called a hash address (hash). Traditionally, hashing is applied to disk files as one of the means to reduce access time. However, this general method can also be applied to access sparse arrays. In the previous example with an array of pointers, a special form of hashing was used, which is called direct addressing . In it, each key corresponds to one and only one cell of the array [1]. In other words, each index calculated by hashing is unique. (When representing a sparse array as an array of pointers, the hash function does not have to implement direct addressing — it was just an obvious approach to implementing a spreadsheet.) In real life, direct hashing schemes are rare; usually a more flexible method is required. This section shows how you can generalize the hashing method, giving it greater power and flexibility.
In the example with a spreadsheet, it is clear that even in the most difficult cases, not all table cells are used. Suppose that in almost all cases the actually occupied cells make up no more than 10 percent of the potentially available places. This means that if the table has a size of 260x100 (2`600 cells), only about 260 cells will be used at any given time. This implies that the largest array that will be needed to store all occupied cells will normally consist of only 260 elements. But how do cells of a logical array match this smaller physical array? And what happens when this array is full? Below is one of the possible solutions.
When a user enters data in a cell of a spreadsheet (i.e., fills an element of a logical array), the position of the cell, determined by its name, is used to obtain an index (hash address) in a smaller physical array. When hashing is performed, the physical array is also called the primary array.. The index in the primary array is obtained from the cell name, which is converted to a number, just as in the example with the array of pointers. But then this number is divided by 10, resulting in the initial entry point to the primary array. (Remember that in this case the size of the physical array is only 10% of the size of the logical array.) If the cell of the physical array is free at this index, the logical index and data are entered into it. But since 10 logical positions correspond to one physical position, collisions may occur when calculating hash addresses [2] . When this happens, the entries are stored in a linked list, sometimes called a collision list.(collision list). Each cell of the primary array is associated with a separate list of collisions. Of course, before the occurrence of a collision, these lists have zero length, as shown in Fig. 23.3.
Fig. 23.3. Hash Example
Pointer
on
list
Conflict index
+ ------ + ---------- + + - + + - +
0 |A1 | --------> | B1 | ---> | C1 |
+ ------ + ---------- + + - + + - +
1 |L1 | --------> | P1 |
+ ------ + ---------- + + - +
2 |A2 | NULL |
+ ------ + ---------- +
3 |M2 | NULL |
+ ------ + ---------- +
4 | | NULL |
+ ------ + ---------- + Order
| . | receipts:
| . | A1
| . | L1
+ ------ + ---------- + B1
258 | A1 | NULL | C1
+ ------ + ---------- + P1
259 | A1 | NULL | A2
+ ------ + ---------- + M2
Primary array
|
Suppose you want to find an element in a physical array by its logical index. First, it is necessary to convert the logical index to the corresponding value of the hash address and check whether the logical index stored in the resulting position of the physical array matches the desired one. If yes, information can be retrieved. Otherwise, it is necessary to view the list of collisions for this position until the required logical index is found or until the end of the chain is reached.
The hash example uses an array of structures called primary:
#define MAX 260
struct htype {
int index; / * logical index * /
int val; / * actual value of the data element * /
struct htype * next; / * pointer to the next item with the same
hash address * /
} primary [MAX];
Before using this array, you must initialize it. The following function assigns the field a indexvalue of -1 (a value that by definition will never be generated as an index); this value indicates an empty element. The value NULLin the field nextcorresponds to an empty hash chain [3] .
/ * Initialize the hash array. * /
void init (void)
{
register int i;
for (i = 0; i
primary [i] .index = -1;
primary [i] .next = NULL; / * empty string * /
primary [i] .val = 0;
}
}
The procedure store()converts the cell name to a hash address in the primary array primary. If the position pointed to by the hash address is occupied, the procedure automatically adds an entry to the list of collisions using the modified version of the function slstore()from the previous chapter. The logical index is also preserved, since it will be needed when retrieving the item. These features are shown below:
/ * Calculate hash address and store value. * /
void store (char * cell_name, int v)
{
int h, loc;
struct htype * p;
/ * Getting the hash address * /
loc = * cell_name - 'A'; / * column * /
loc + = (atoi (& cell_name [1]) - 1) * 26; / * string * width + column * /
h = loc / 10; / * hash * /
/ * Save to received position if it is not occupied.
or if the logical indices are the same - that is, when updating.
* /
if (primary [h] .index == - 1 || primary [h] .index == loc) {
primary [h] .index = loc;
primary [h] .val = v;
return;
}
/ * otherwise, create a collision list
or add to engo element * /
p = (struct htype *) malloc (sizeof (struct htype));
if (! p) {
printf ("Out of memory \ n");
return;
}
p-> index = loc;
p-> val = v;
slstore (p, & primary [h]);
}
/ * Adding items to the collision list. * /
void slstore (struct htype * i,
struct htype * start)
{
struct htype * old, * p;
old = start;
/ * find the end of the list * /
while (start) {
old = start;
start = start-> next;
}
/ * associate with new entry * /
old-> next = i;
i-> next = NULL;
}
In order to get the value of an element, the program must first calculate the hash address and check whether the logical index stored in the received position of the physical array coincides with the desired logical index. If it matches, it returns the value of the cell; otherwise, the search is performed in the list of collisions. The function find()that performs these tasks is shown below:
/ * Calculating the hash address and getting the value. * /
int find (char * cell_name)
{
int h, loc;
struct htype * p;
/ * get hash value * /
loc = * cell_name - 'A'; / * column * /
loc + = (atoi (& cell_name [1]) - 1) * 26; / * string * width + column * /
h = loc / 10;
/ * return value if cell is found * /
if (primary [h] .index == loc) return (primary [h] .val);
else {/ * otherwise see a list of collisions * /
p = primary [h] .next;
while (p) {
if (p-> index == loc) return p-> val;
p = p-> next;
}
printf ("No cells in the array \ n");
return -1;
}
}
Creating a delete function is left to the reader as an exercise. ( Hint : Just reverse the insertion process.)
The hashing algorithm shown above is very simple. As a rule, in practice, more complex methods are used to ensure a more uniform distribution of indices in the primary array, which eliminates long hash chains. However, the basic principle remains the same.
At best (quite rare), each physical index calculated by the hash function is unique, and the access time is approximately equal to the access time for direct addressing. This means that collision lists are not created, and all sampling operations are essentially direct access operations. However, this is rarely the case, since for this it is required that the logical indices are evenly distributed in the space of physical indices. In the worst case (also rare), the hashing scheme degenerates into a linked list. This happens when the hash addresses of all logical indexes match. On average (and most likely), the access time for hashing is equal to the access time for direct addressing plus some constant proportional to the average length of the hashing chains.The most important factor in the implementation of sparse arrays by the method of hashing is the choice of such a hashing algorithm, in which physical indices are evenly distributed, thus avoiding the formation of long lists of collisions.
[1] In other words, the hash function is a bijection.
[2] That is, situations where the same hash address corresponds to different keys k 1 ≠ k 2 : h (k 1 ) = h (k 2 ) (here h is a hash function).
[3] The hash chain is a chain connecting the elements of a hash table with the same hash code. Earlier, the author called her a collision list (collision list). Sometimes it is also called an overflow package .
When choosing one of the methods for representing a sparse array — using a linked list, binary tree, pointer array, or hashing — you must be guided by the requirements for speed and efficient use of memory. In addition, it is necessary to take into account how dense the sparse array will be filled.
If the logical array is filled very rarely, linked lists and binary trees are the most efficient in terms of memory usage, since they allocate memory only for those elements that are actually used. The links themselves require very little additional memory, which can usually be neglected. Representation in the form of an array of pointers involves the creation of the entire array of pointers, even if some elements are not used. In this case, the memory should not only fit the entire array, but also should remain free memory for the application. In some cases this can be a serious problem. You can usually estimate in advance the approximate amount of free memory and decide whether it is sufficient for your program.The hashing method takes an intermediate position between views using an array of pointers and a linked list or binary tree. Despite the fact that the entire primary array, even if it is not used, must be in memory, this array will still be smaller than the array of pointers.
If the logical array is filled fairly densely, the situation changes significantly. In this case, creating an array of pointers and hashing becomes more acceptable methods. Moreover, the search time for an element in the array of pointers is constant and does not depend on the degree of filling of the logical array. Although the search time for hashing is not constant, it is bounded above by some small value. But in the case of a linked list and a binary tree, the average search time increases as the array is filled. This should be remembered if access time is a critical factor.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.