Lecture
In general, sorting should be understood as the process of regrouping a given set of objects in a certain order. The purpose of sorting is to facilitate the subsequent search for elements in such a sorted set. It is almost universal, fundamental activity. We meet with sorted objects in phone books, in income tax lists, in table of contents of books, in libraries, in dictionaries, in warehouses almost everywhere where it is necessary to search for stored objects. Even kids are taught to keep their things "in order," and they already face some sort of sorting long before they become familiar with the basics of arithmetic.
Thus, talking about sorting is appropriate and important when it comes to data processing. What can be easier to sort than data? Nevertheless, our initial interest in sorting is based on the fact that when building algorithms we encounter many very fundamental techniques. There are almost no methods that are not encountered when discussing this problem. In particular, sorting is an ideal object for demonstrating a huge variety of algorithms, all of them are invented for the same task, many in some sense are optimal, most have their merits. Therefore, it is also an ideal object, demonstrating the need to analyze the performance of algorithms. Moreover, with examples of sorting, it is possible to show how by complicating the algorithm, although there are already obvious methods at hand, one can achieve a significant gain in efficiency.
The choice of the algorithm depends on the structure of the data being processed is almost a law, but in the case of sorting this dependence is so deep that the corresponding methods were even divided into two classes: sorting arrays and sorting sequence files. Sometimes they are called internal and external sorting, because arrays are stored in fast RAM, internal memory of a machine with random access, and files are usually placed in slower, but more capacious external memory, on devices based on mechanical movements of disks or tapes. Already by the example of sorting numbered cards, a significant difference in these approaches becomes apparent. If the cards are "lined up" in the form of an array, then they seem to lie before the sorting, he sees each of them and has access to it. If the cards form a file, then this assumes that only the top card is visible in each of the stacks. This restriction, of course, will seriously affect the sorting method, but nothing can be done: there can be so many cards that they all do not fit on the table.
Before going further, we introduce some concepts and notation. We will use them further. If we have elements a1, a2, ..., аn, then sorting is a permutation of these elements array ak1, ak2, ..., akn, where for some ordering function f the relations f ak1 <= f ak2 <= are fulfilled .. . <= f аkn.
Usually, the ordering function is not calculated by any rule, but is stored as an explicit component of the field of each element. Its value is called the item key keu. Therefore, such formations as recording are well suited for the presentation of elements, and graphically it appears as follows (Fig. 1):
Speaking of sorting algorithms, we will pay attention only to the component - the key, while other components can even not be defined (Fig. 2). Therefore, from our further considerations all the related information. To reduce these costs, sorting is done in the key address table. After sorting, reset the pointers. This is the method of sorting the address table (Fig. 3). A sorting method is called stable if the sorting process does not change the relative position of elements with equal keys. Stability of sorting is often desirable if we are talking about elements that are already ordered (sorted) by some secondary keys (i.e. properties) that do not affect the primary key. 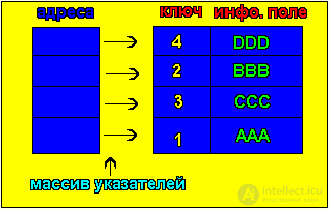
Sorted array (Fig. 2): 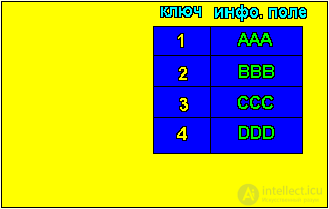
Array sorted by another method (Fig. 3): 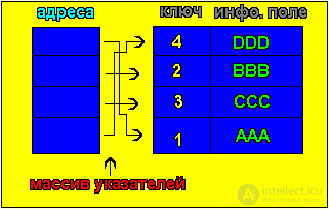
The main condition: the selected method of sorting arrays must economically use the available memory. This implies that permutations that put the elements in order should be performed at the same place, i.e. methods in which elements from array A are transferred to the resulting array H are of much lower interest. By limiting the criterion of saving our memory to the choice of the desired method among the many possible, we will first classify the methods according to their economy, on the time of their work. A good measure of efficiency can be C - the number of necessary comparisons of keys and M - the number of shipments (permutations) of elements.
These numbers are functions of the n-number of elements to be sorted. Although the improved sorting algorithms require the order of n * log n comparisons, we will examine a simple method that is referred to as the so-called direct method, where the order of n ^ 2 key comparisons is required. The advantages of direct methods include:
1. Direct methods are especially convenient for explaining the characteristic features of the basic principles of most sorts.
2. The programs of these methods are easy to understand, and they are short. Recall that the programs themselves also take up memory.
3. Improved methods require a small number of operations, but these operations are usually more complex, and therefore for sufficiently small n, direct methods turn out to be faster, although for large n, they should not be used, of course.
Sorting methods "in the same place" can be divided according to their defining principles into three main categories:
1. Sorting by direct switching on the insertion.
2. Sorting direct selection By selection.
3. Sorting direct exchange Bü exchange.
Direct methods include direct selection.
Consider the entire array row and select an element smaller or larger than element a (i), determine its place in the array - k, and then swap element a (i) and element a (k).
for i = 1 to n - 1
x = a (i)
k = i
for j = i + 1 to n
if x> a (j) then
k = j
x = a (k)
endif
next j
a (k) = a (i)
a (i) = x
next i
return
for i: = 1 to n - 1 do
begin
x: = a [i];
k: = i;
for j: = i + 1 to n do
if x> a [j] then
begin
k: = j;
x: = a [k];
end;
a [k]: = a [i];
a [i]: = x;
end;
Efficiency of the algorithm:
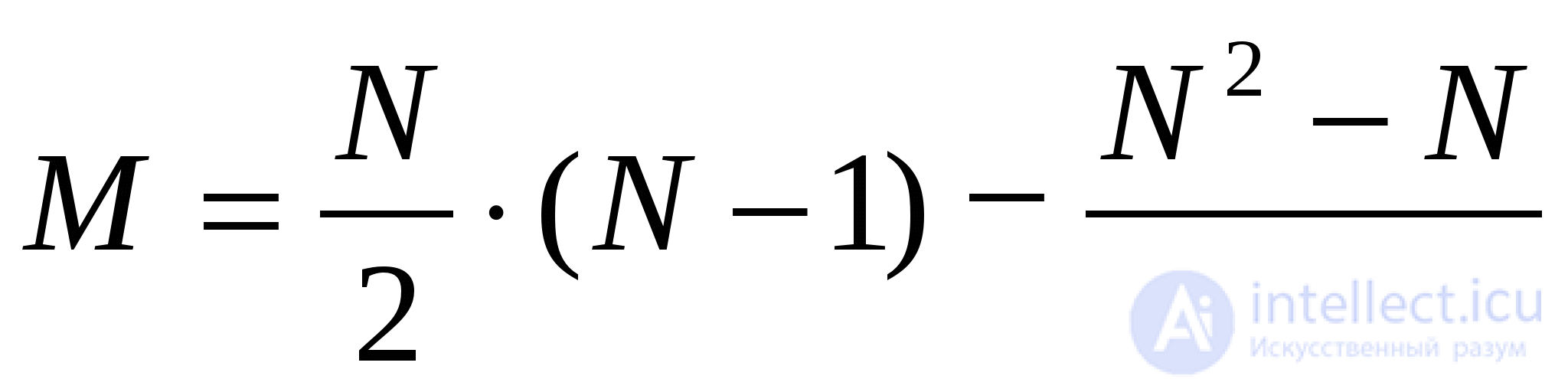
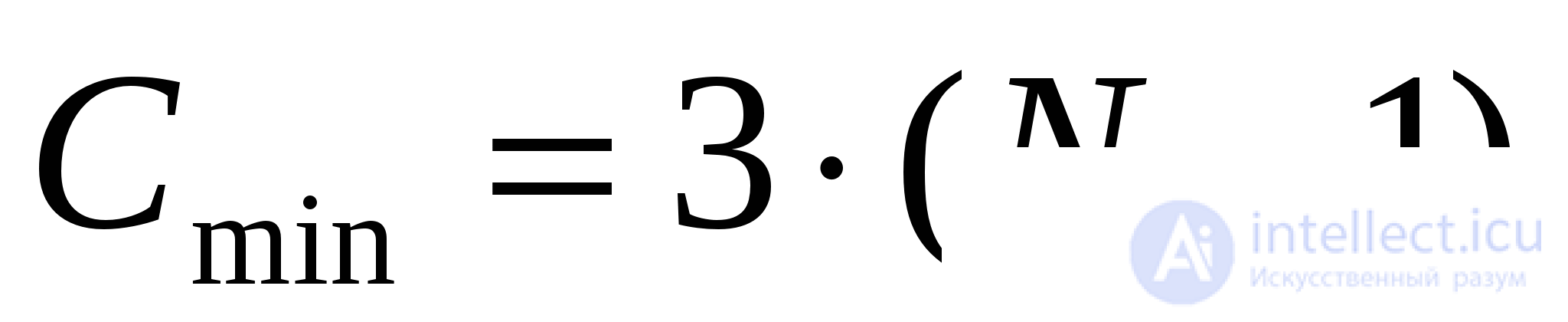
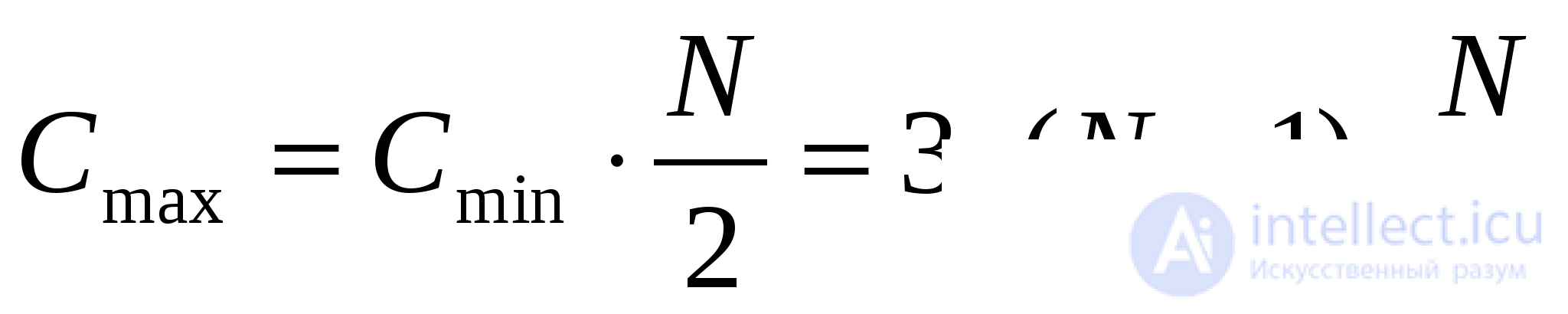
In the worst case, sorting by direct choice gives the order of n 2 , as for the number of comparisons, and for the number of displacements.
Create a group of N students. Enter them: last name, first name, year of birth, assessment of subjects: p. And al., Higher. mathematics, physics, programming, the total score of the session; Develop a program using the method of "direct selection", which would carry out the sorting (according to option):
1. Names of students alphabetically.
2. Names of students alphabetically in reverse order.
3. Seniority students (starting from the oldest).
4. Seniority students (starting from the youngest).
5. Students on a general score (ascending).
6. Students by total score (descending).
7. Students according to the results of the 1st exam (ascending).
8. Students according to the results of the 2nd exam (descending).
9. Students according to the results of the 3rd exam (ascending).
10. Students according to the results of the 4th exam (descending).
11. Names in alphabetical order.
12. Names in reverse alphabetical order.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.