Lecture
By elementary data structures we mean data structures that are either provided directly by a computer or modeled by computer using data types available at the computer level. Thus, any basic computer data structure can be called the elementary data structure. Below will be considered such as an array and a linked list. It should be noted that they can be considered atomic data structures, since they are not supposed to be simulated using other elementary data structures. Although this possibility exists from a computer point of view, the constructed implementation will not give a tangible gain over the system data structure, since it obviously leads to a decrease in the efficiency of some of the basic operations, such as inserting and deleting an element.
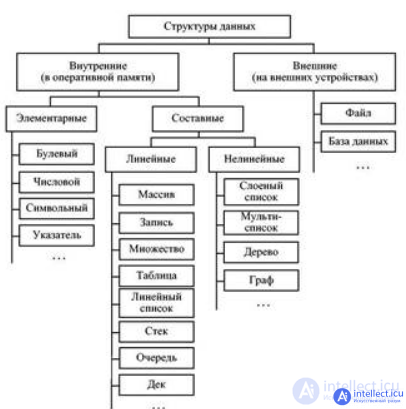
rice data structure classification
An array is a linear, homogeneous, elementary data structure, which is a continuous ordered sequence of memory cells and designed to store data of the same type. Access to the elements of the array is carried out by index or by a set of indices, where by index we mean some integer value. In general, an array is a multidimensional parallelepiped, in which the measurement values can be different. An array with measurements will be called m-dimensional and denoted by, where is the number of elements that can be written at the level. Thus, an array with measurements allows you to store elements with memory costs inside, where is the number of memory cells required to store one element. As noted earlier, any array is a continuous section of memory,therefore, a multidimensional array is technically a one-dimensional array, access to the elements of which is carried out according to the following formula:
In the following presentation, we will assume that the indexing of the elements of the array begins with unity, unless otherwise specified. The procedure for calculating the corresponding index according to the above expression is presented below (procedure
Procedure 2.1.1. Get index
Get Index Impl (i1, i2, ..., im) index = 0 for j = 1 to m - 1 do index = (index + ij) * nj + 1 index = index + im return index
Consider the basic operations that allow you to manipulate data stored in an array, without loss of generality, we assume that a one-dimensional array consisting of elements is specified: 1) reading / writing of an element takes time, since the array is a random access data structure; 2) the complexity of the search for elements in the array depends on whether it is ordered or not: in the case of an ordered array, the search the necessary data can be implemented in operations, otherwise operations in the worst case will be required; 3) inserting / deleting elements into an array requires operations in the worst case, since changing the structure of an array requires moving elements. This is evidenced by the site https://intellect.icu. If the insertion and removal of elements is carried out only at the end of the array, then the complexity of the operations will be. The algorithm for inserting an element into an array is given below (procedure 2).
Procedure 2. Array: Insert
Insert Impl (A, index, element) if index> 0 then for i = n downto index do A [i + 1] = A [i] A [index] = element
In conclusion, we emphasize once again that a multidimensional array can be implicitly regarded as an array of arrays of the same size. At the same time, there is the concept of a torn array *, the use of which is justified if its elements are arrays of arbitrary length and it should be clearly indicated that it consists of arrays. In this case, the torn array will be denoted as. An example of a torn array is shown below (Fig. 2.1):
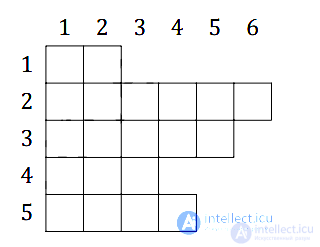
Fig. 2.1. Torn Array Example
It should be noted that most modern imperative programming languages have the ability to work with arrays. Some of the languages provide opportunities for creating torn arrays as one of the data types.
As noted above, the operations of inserting and deleting an element into an array are performed in the worst case, for operations. Therefore, there is a need to develop data structures that will get rid of this drawback and, as a result, provide effective methods for the inclusion / exclusion of elements. The advantages of the array include the economical memory consumption required for data storage, as well as
fast access time to array elements. Consequently, the use of arrays is justified if the data are accessed by an integer index and in some cases not involving modification of the data set by increasing / decreasing the number of its elements.
2.1.2. Linked Lists
A linked list is a linear, homogeneous, elementary data structure designed to store data of the same type, in which the order of objects is determined by pointers. Unlike an array, a linked list, as follows from this definition, stores items optionally in consecutive memory cells. This property is justified by the name “Linked List” of the data structure under consideration, since they are connected with the help of memory cell pointers into a single whole. Considering a linked list, we will assume that its element is described by a composite data type that stores user data of some type and a pointer to the next element of the list. In a linked list, it is customary to distinguish between the end elements: the head is the start element of the list, the tail is the end. In this way,The recursive description of the linked list is as follows (procedure 3):
Procedure .3. Linked List
Type linkedListElement
{
item: T
linkedList
}
linkedList
{
head: linkedListElement
tail: linkedListElement
}
emptyLinkedList = linkedList
{
head = null
tail = null
}
In addition to user data and pointers to neighboring elements, a list item can also store some overhead information dictated by the specifics of the task (for example, the time the list item was created, the address of the item in memory, information about the owner, etc.). In practice, most often all kinds of linked lists are used, which are mostly due to the peculiarities of iterating over the list. The main ones are singly connected, doubly connected, and ring lists, which will be discussed below together with the basic set of operations. If this does not lead to contradictions, then an empty list will be denoted by a symbol.
A simply linked list is a linked list in which each of the elements of the list contains a pointer directly to the next element of the same list. A singly linked list is the simplest kind of linked list, since each of its elements involves storing minimal information for linking list items into a single structure. You can see that this definition is identical to the definition of a linked list, so their description will be similar.
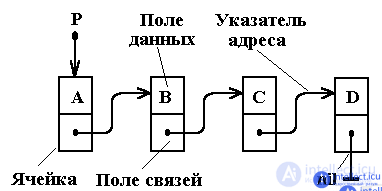
By a doubly linked list we mean a linked list in which each of the elements contains a pointer to both the next element of the list and the previous one.
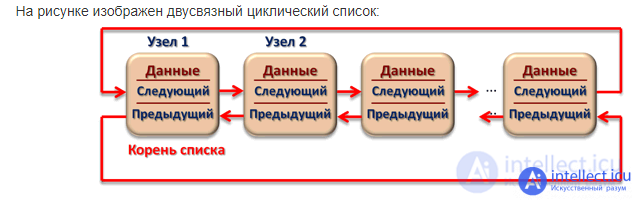
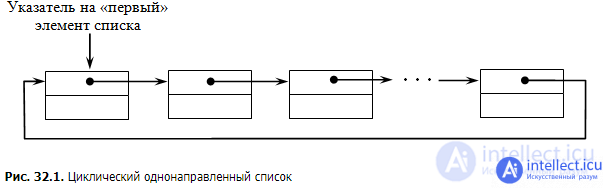
Ring lists
A ring list is a linked list in which the last element refers to the first. Typically, ring lists are based on either singly linked or doubly linked lists. Due to the fact that the list is closed in a ring, only one pointer is required that will determine the entry point to the list. Implementations of basic operations for a ring list are not given because of the great similarity with the corresponding operations for a singly linked list. The main advantages of ring lists should include the ability to view all elements of the list, starting with an arbitrary one, as well as quick access to the first and last elements if the list is implemented on the basis of a doubly linked list.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.