Lecture
Dynamic structures, by definition, are characterized by the lack of physical contiguity of the structure elements in memory by the inconstancy and unpredictability of the size (number of elements) of the structure during its processing. In this section, the features of dynamic structures, determined by their first characteristic property, are considered. The features associated with the second property are discussed in the last section of this chapter.
Since the elements of a dynamic structure are located at unpredictable memory addresses, the address of an element of such a structure cannot be calculated from the address of the initial or previous element. To establish the connection between the elements of the dynamic structure, pointers are used through which explicit links are established between the elements. Such a representation of data in memory is called connected. The element of a dynamic structure consists of two fields:
When a coherent presentation of data is used to solve an application problem, for the end user, only the content of the information field is made visible, and the field of bundles is used only by the programmer-developer.
The merits of a coherent presentation of data is the ability to provide significant variability in structures;
At the same time, a coherent presentation is not without flaws, the main ones are:
The last drawback is the most serious and it is they who limit the applicability of the coherent view of data. If in the adjacent data representation, in all cases it was enough for us to calculate the address of any element and the element number and information contained in the structure descriptor, then for the connected representation, the element address cannot be calculated from the original data. The handle of the connected structure contains one or more pointers to enter the structure, then the search for the desired element is performed by following the chain of pointers from element to element. Therefore, a coherent representation is almost never used in tasks where a logical data structure has the form of a vector or an array — with access by element number, but it is often used in tasks where the logical structure requires other initial access information (tables, lists, trees, etc. .).
A list is an ordered set consisting of a variable number of elements to which the include and exclude operations apply. A list that reflects the neighborhood relations between elements is called linear. We discussed logical lists in Chapter 4, but there we talked about semi-static data structures and restrictions on the size of the list were imposed. If restrictions on the length of the list are not allowed, the list is represented in memory as a coherent structure. Linear connected lists are the simplest dynamic data structures.
Graphically, links in lists are conveniently depicted using arrows. If the component is not related to any other, then a value is written in the pointer field, not indicating any element. Such a link is denoted by a special name - nil.
5.2.1. Machine Representation of Connected Linear Lists
In fig. 5.1 shows the structure of a single-linked list. On it, the INF field is an information field, data, NEXT is a pointer to the next element of the list. Each list must have a special element called the list start indicator or a list head, which is usually different in format from the other elements. In the index field of the last element of the list is a special sign nil, indicating the end of the list.

Fig.5.1. The structure of a single-linked list
However, processing a single-linked list is not always convenient, since there is no possibility of moving in the opposite direction. This possibility is provided by a doubly linked list, each element of which contains two pointers: to the next and previous elements of the list. The structure of a linear doubly linked list is shown in Fig. 5.2, where the NEXT field is a pointer to the next element, the PREV field is a pointer to the previous element. In the extreme elements, the corresponding pointers must contain nil, as shown in Fig. 5.2.
For the convenience of processing the list add another special element - the pointer to the end of the list. The presence of two pointers in each element complicates the list and leads to additional memory costs, but at the same time provides more efficient execution of some list operations.
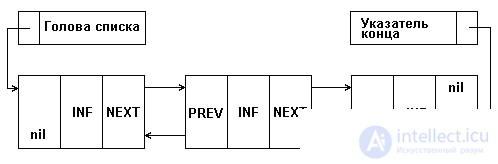
Fig.5.2. Double link structure
A variation of the considered types of linear lists is a ring list, which can be organized on the basis of both simply-connected and doubly-connected lists. In this case, in a simply linked list, the pointer of the last element must point to the first element; in a doubly linked list in the first and last elements, the corresponding pointers are redefined, as shown in Figure 5.5.
When working with such lists, some procedures that are performed on the list are somewhat simplified. However, when viewing such a list, some precautions should be taken to avoid falling into an infinite loop.
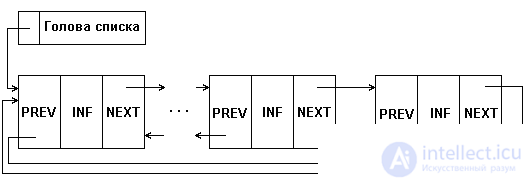
Fig.5.3. The structure of a ring double-linked list
In memory, the list is a collection of a descriptor and records of the same size and format placed arbitrarily in a certain area of memory and connected to each other in a linearly ordered chain using pointers. A record contains information fields and fields of pointers to neighboring elements of the list, and some fields of the information part may be pointers to memory blocks with additional information relating to the list element. The list descriptor is implemented as a special record and contains such information about the list as the address of the beginning of the list, the structure code, the name of the list, the current number of elements in the list, the description of the element, etc., etc. The descriptor may be in the same area of memory in which the elements of the list are located, or some other place is allocated for it.
5.2.2. Implementation of operations on connected linear lists
The following are some simple linear list operations. The execution of operations is illustrated in the general case with drawings with schemes for changing links and program examples.
In all the figures, the solid lines show the connections that existed before execution and remained after the operation was performed. The dotted line shows the connections established during the operation. The 'x' is marked with links broken during the operation. In all operations, the sequence of correction of pointers is extremely important, which ensures the correct change of the list, not affecting other elements. With the wrong order of correction is easy to lose part of the list. Therefore, the pictures next to the established links in brackets show the steps in which these links are established.
In the software examples, the following data types are defined:
type
sllptr = ^ slltype; {pointer in a single-linked list}
slltype = record {single-linked list element}
inf: data; {information part}
next: sllptr; {pointer to the next element}
end;
type
dllptr = ^ dlltype; {pointer in a doubly linked list}
dlltype = record {single-linked list element}
inf: data; {information part}
next: sllptr; {pointer to the next item (forward)}
prev: sllptr; {pointer to the previous item (back)}
end;
Verbal descriptions of algorithms are given in the form of comments to software examples.
In the general case, the examples should show the implementation of each operation for the lists: a simply connected linear, simply connected ring, two-connected linear, doubly connected ring. The volume of our publication does not allow to give a complete set of examples; we provide the reader with the development of missing examples.
Enumerate list items.
This operation, perhaps more often than others, is performed on linear lists. When it is executed, sequential access to the elements of the list is performed - to all until the end of the list or until the search element is found.
The search algorithm for a single-linked list is represented by software example 5.1.
{==== Software Example 5.1 ====}
{Enumeration of 1-linked list}
Procedure LookSll (head: sllptr);
{head - pointer to the beginning of the list}
var cur: sllptr; {current element address}
begin
cur: = head; {1st list item is set to be current}
while cur <> nil do begin
{the informational part of that email is being processed
which cur points to.
Processing may consist of:
}
cur: = cur ^ .next;
{the pointer to the next el-t is selected from the current one and for the next iteration the next one becomes the current one; if the current item was the last one, then its next field contains a null pointer, and so on. in cur, nil is written, which will lead to exit from the loop while checking the condition while} end; end;
In a doubly linked list, the search is possible both in the forward direction (it looks exactly the same as the search in the simply connected list) and in the reverse. In the latter case, the procedure parameter should be tail - a pointer to the end of the list, and the transition to the next element should be carried out by a pointer back:
cur: = cur ^ .prev;
In the ring list, the end of the search should not occur on the basis of the last element - such a sign is absent, but on reaching the element from which the search began. The brute-force algorithms for the doubly-connected and ring list are left to the reader for independent development.
Insert item into the list.
Inserting an element in the middle of a single-linked list is shown in Figure 5.4 and Example 5.2.
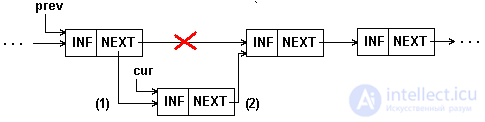
Fig.5.4. Insert an item in the middle of a 1-linked list
{==== Software Example 5.2 ====}
{Insert an item in the middle of a 1-linked list}
Procedure InsertSll (prev: sllptr; inf: data);
{prev - the address of the previous email; inf - new el data}
var cur: sllptr; {new email address}
begin
{allocation of memory for a new element and entry in its inf. part}
New (cur); cur ^ .inf: = inf;
cur ^ .next: = prev ^ .next; {el following next
will follow the new}
prev ^ .next: = cur; {new el follows the previous one}
end;
Figure 5.5 represents an insertion in a doubly linked list.
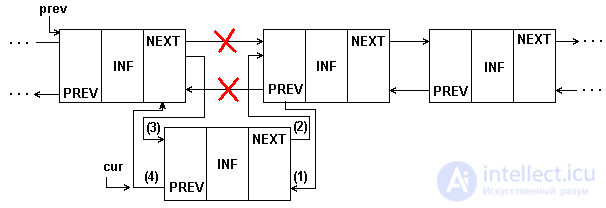
Fig.5.5. Insert an item in the middle of a 2-link list
The examples provided provide an insertion in the middle of the list, but cannot be applied to the insert at the top of the list. With the latter, the pointer to the beginning of the list should be modified, as shown in Fig.5.6.
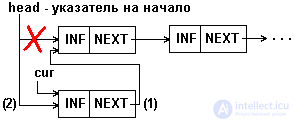
Fig.5.6. Insert an item at the beginning of a 1-linked list
Program example 5.3 represents a procedure that performs the insertion of an element anywhere in a single-linked list.
{==== Software Example 5.3 ====}
{Insert an item anywhere in the 1-linked list}
Procedure InsertSll
var head: sllptr; {pointer to the beginning of the list, may change in
procedure, if head = nil - the list is empty}
prev: sllptr; {pointer to the item, after which an insert is made,
if prev-nil - insertion before the 1st e-volume}
inf: data {- new email data}
var cur: sllptr; {new email address}
begin
{allocation of memory for a new element and entry in its inf. part}
New (cur); cur ^ .inf: = inf;
if prev <> nil then begin {if there is a previous email, insert it in
the middle of the list, see note 5.2}
cur ^ .next: = prev ^ .next; prev ^ .next: = cur;
end
else begin {insert at the beginning of the list}
cur ^ .next: = head; {new email indicates the former 1st list email;
if head = nil, then the new email will be the last email of the list}
head: = cur; {new el-t becomes the 1st in the list, pointer to
the beginning now points to him}
end; end;
Remove item from list.
Removing an element from a single-linked list is shown in Figure 5.7.
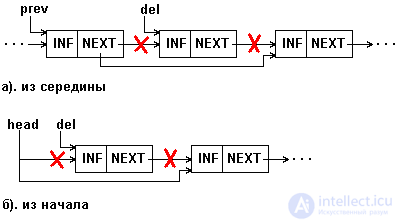
Fig.5.7. Deleting an item from a 1-linked list
Obviously, the deletion procedure is easy to perform if the address of the element preceding the deleted one is known (prev in Figure 5.7.a). We, however, in fig. 5.7 and in Example 5.4 we give the procedure for the case when the element to be deleted is specified by its address (del in Figure 5.7). The procedure provides for deleting both from the middle and from the beginning of the list.
{==== Software Example 5.4 ====}
{Deleting an item from anywhere in a 1-linked list}
Procedure DeleteSll (
var head: sllptr; {pointer to the beginning of the list, can
change in procedure}
del: sllptr {the pointer to the item that is deleted});
var prev: sllptr; {previous email address}
begin
if head = nil then begin {attempt to remove from empty list
regarded as an error (in the following examples this case
will be taken into account)}
Writeln ('Error!'); Halt;
end;
if del = head then {if the deleted item is the 1st in the list, then
the next one becomes the first}
head: = del ^ .next
else begin {remove from the middle of the list}
{it is necessary to search for the el preceding the deleted one; the search is performed by enumerating the list from the very beginning until it finds an email, the next field matches the address of the element to be deleted}
prev: = head ^ .next;
while (prev ^ .next <> del) and (prev ^ .next <> nil) do
prev: = prev ^ .next;
if prev ^ .next = nil then begin
{this is the case when the entire list has been moved, but the email was not found, it is not in the list; regarded as an error (in the following examples this case will be taken into account)}
Writeln ('Error!'); Halt;
end;
prev ^ .next: = del ^ .next; {previous email now indicates
next to delete}
end;
{item is excluded from the list, now you can free
his memory}
Dispose (del);
end;
Removing an item from a doubly linked list requires correction of a larger number of pointers, as shown in Figure 5.8.
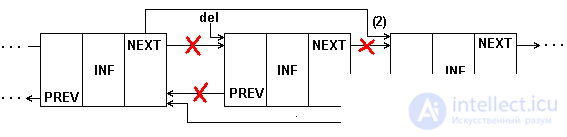
Fig.5.8. Deleting an item from a 2-linked list
The procedure for removing an item from a doubly linked list will be even easier than for a simply connected one, since it does not need to search for the previous item; it is selected by the backward pointer.
Swap items in the list.
The variability of dynamic data structures involves not only changes in the size of the structure, but also changes in the relationships between elements. For connected structures, changing connections does not require sending data in memory, but only changing pointers in the elements of a connected structure. As an example, the permutation of two adjacent elements of the list is given. In the permutation algorithm in a simply connected list (Fig. 5.9, Example 5.5), it was assumed that the address of the element preceding the pair in which the permutation is made is known. The algorithm also does not take into account the case of permutation of the first and second elements.

Fig.5.9. Permutation of neighboring elements of a 1-linked list
{==== Software Example 5.5 ====}
{Permutation of two adjacent elements in a 1-linked list}
Procedure ExchangeSll (
prev: sllptr {pointer to the element preceding
rearranged pair});
var p1, p2: sllptr; {pointers to e-couples}
begin
p1: = prev ^ .next; {pointer to the 1st el-t of the pair}
p2: = p1 ^ .next; {pointer to the 2nd el-t pair}
p1 ^ .next: = p2 ^ .next; {1st element of the pair now indicates
following the pair}
p2 ^ .next: = p1; {1st el pair now follows 2nd}
prev ^ .next: = p2; {2nd el-pair now becomes 1st}
end;
In the permutation procedure for a doubly linked list (Fig.5.10.), It is easy to take into account the permutation at the beginning / end of the list.
Copy part of the list.
When copying, the original list is stored in memory, and a new list is created. The information fields of the elements of the new list contain the same data as in the elements of the old list, but the bundle fields in the new list are completely different, since the elements of the new list are located at different addresses in memory. It is significant that the copy operation involves duplication of data in memory. If after creating a copy the data in the original list is changed, the change will not be reflected in the copy and vice versa.
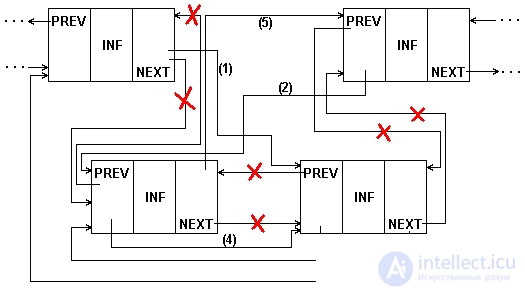
Fig.5.10. Rearrange the neighboring elements of a 2-linked list
Copying for a single-linked list is shown in program example 5.6.
{==== Software Example 5.6 ====}
{Copy part of a 1-linked list. head - pointer to
the beginning of the copied part; num is the number of el. F-tion returns
pointer to copy list}
Function CopySll (head: sllptr; num: integer): sllptr;
var cur, head2, cur2, prev2: sllptr;
begin
if head = nil then {the source list is empty - the copy is empty}
CopySll: = nil
else begin
cur: = head; prev2: = nil;
{brute force source list to the end or on the num counter}
while (num> 0) and (cur <> nil) do begin
{allocating memory for the output list item and writing to it
information part}
New (cur2); cur2 ^ .inf: = cur ^ .inf;
{if the 1st el-t of the output list - the pointer to
start, otherwise - the pointer is written to the previous element}
if prev2 <> nil then prev2 ^ .next: = cur2 else head2: = cur2;
prev2: = cur2; {current el becomes previous}
cur: = cur ^ .next; {promotion on the original list}
num: = num-1; {counting email}
end;
cur2 ^ .next: = nil; {null pointer - last email
output list}
CopySll: = head2; {return a pointer to the beginning of the exit list}
end; end;
Merge two lists.
The merge operation consists of forming one list from two lists - it is similar to the string concatenation operation. In the case of a single-linked list shown in Example 5.7, the merging is very simple. The last element of the first list contains a null pointer to the next element, this pointer is a sign of the end of the list. Instead, a null pointer is placed in the last element of the first list with a pointer to the beginning of the second list. Thus, the second list becomes a continuation of the first.
{==== Software Example 5.7 ====}
{Merge two lists. head1 and head2 are pointers to beginnings
lists. The resulting list is indicated by head1}
Procedure Unite (var head1, head2: sllptr);
var cur: sllptr;
begin {if the 2nd list is empty - nothing to do}
if head2 <> nil then begin
{if the 1st list is empty, the output list will be the 2nd}
if head1 = nil then head1: = head2
else {enumeration of the 1st list to the last of its email}
begin cur: = head1;
while cur ^ .next <> nil do cur: = cur ^ .next;
{last item of the 1st list indicates the beginning of the 2nd}
cur ^ .next: = head2;
end;head2: = nil; {2nd list is canceled}
end; end;
5.2.3. Applying linear lists
Линейные списки находят широкое применение в приложениях, где непредсказуемы требования на размер памяти, необходимой для хранения данных; большое число сложных операций над данными, особенно включений и исключений. На базе линейных списков могут строится стеки, очереди и деки. Представление очереди с помощью линейного списка позволяет достаточно просто обеспечить любые желаемые дисциплины обслуживания очереди. Особенно это удобно, когда число элементов в очереди трудно предсказуемо.
В программном примере 5.8 показана организация стека на односвязном линейном списке. Это пример функционально аналогичен примеру 4.1 с той существенной разницей, что размер стека здесь практически неограничен.
Стек представляется как линейный список, в котором включение элементов всегда производятся в начала списка, а исключение - также из начала. Для представления его нам достаточно иметь один указатель - top, который всегда указывает на последний записанный в стек элемент. В исходном состоянии (при пустом стеке) указатель top - пустой. Процедуры StackPush и StackPop сводятся к включению и исключению элемента в начало списка. Обратите внимание, что при включении элемента для него выделяется память, а при исключении - освобождается. Перед включением элемента проверяется доступный объем памяти, и если он не позволяет выделить память для нового элемента, стек считается заполненным. При очистке стека последовательно просматривается весь список и уничтожаются его элементы. При списковом представлении стека оказывается непросто определить размер стека. Эта операция могла бы потребовать перебора всего списка с подсчета числа элементов. Чтобы избежать последовательного перебора всего списка мы ввели дополнительную переменную stsize, которая отражает текущее число элементов в стеке и корректируется при каждом включении/исключении.
{==== Software Example 5.8 ====}
{Stack on a 1-connected linear list}
unit stack;
Interface
type data = ...; {emails can be of any type}
Procedure StackInit;
Procedure StackClr;
Function StackPush (a: data): boolean;
Function StackPop (Var a: data): boolean;
Function StackSize: integer;
Implementation
type stptr = ^ stit; {pointer to list email}
stit = record {list item}
inf: data; {data}
next: stptr; {pointer to the next email}
end;
Var top: stptr; {pointer to the top of the stack}
stsize: longint; {stack size}
{** initialization - list is empty}
Procedure StackInit;
begin top: = nil; stsize: = 0; end; {StackInit}
{** clear - free all memory}
Procedure StackClr;
var x: stptr;
begin {brute force emails to the end of the list and destroy them}
while top <> nil do
begin x: = top; top: = top ^ .next; Dispose (x); end;
stsize: = 0;
end; {StackClr}
Function StackPush (a: data): boolean; {paging}
var x: stptr;
begin {if there is no more free memory - failure}
if MaxAvail
else {allocating memory for the element and filling out the information parts}
begin New (x); x ^ .inf: = a;
{new el-t is placed in the head of the list}
x ^ .next: = top; top: = x;
stsize: = stsize + 1; {size correction}
StackPush: = true;
end;
end; {StackPush}
Function StackPop (var a: data): boolean; {stack fetch}
var x: stptr;
begin
{the list is empty - the stack is empty}
if top = nil then StackPop: = false
else begin
a: = top ^ .inf; {selection of information from the 1st e-list}
{1st el is excluded from the list, memory is freed}
x: = top; top: = top ^ .next; Dispose (top);
stsize: = stsize-1; {size correction}
StackPop: = true;
end; end; {StackPop}
Function StackSize : integer; { определение размера стека }
begin StackSize:=stsize; end; { StackSize }
END.
Программный пример для организация на односвязном линейном списке очереди FIFI разработайте самостоятельно. Для линейного списка, представляющего очередь, необходимо будет сохранять: top - на первый элемент списка, и bottom - на последний элемент.
Линейные связные списки иногда используются также для представления таблиц - в тех случаях, когда размер таблицы может существенно изменяться в процессе ее существования. Однако, то обстоятельство, что доступ к элементам связного линейного списка может быть только последовательным, не позволяет применить к такой таблице эффективный двоичный поиск, что существенно ограничивает их применимость. Поскольку упорядоченность такой таблицы не может помочь в организации поиска, задачи сортировки таблиц, представленных линейными связными списками, возникают значительно реже, чем для таблиц в векторном представлении. Однако, в некоторых случаях для таблицы, хотя и не требуется частое выполнение поиска, но задача генерации отчетов требует расположения записей таблицы в некотором порядке. Для упорядочения записей такой таблицы применимы любые алгоритмы из описанных нами в разделе 3.9. Некоторые алгоритмы, возможно, потребуют каких-либо усложнений структуры, например, быструю сортировку Хоара целесообразно проводить только на двухсвязном списке, в цифровой сортировке удобно создавать промежуточные списке для цифровых групп и т.д. Мы приведем два простейших примера сортировки односвязного линейного списка. В обоих случаях мы предполагаем, что определены типы данных:
type lptr = ^item; { указатель на элемент списка }
item = record { элемент списка }
key : integer; { ключ }
inf : data; { данные }
next: lptr; { указатель на элемент списка }
end;
В обоих случаях сортировка ведется по возрастанию ключей. В обоих случаях параметром функции сортировки является указатель на начало неотсортированного списка, функция возвращает указатель на начало отсортированного списка. Прежний, несортированный список перестает существовать.
Пример 5.9 демонстрирует сортировку выборкой. Указатель newh является указателем на начало выходного списка, исходно - пустого. Во входном списке ищется максимальный элемент. Найденный элемент исключается из входного списка и включается в начало выходного списка. Работа алгоритма заканчивается, когда входной список станет пустым. Обратим внимание читателя на несколько особенностей алгоритма. Во-первых, во входном списке ищется всякий раз не минимальный, а максимальный элемент. Поскольку элемент включается в начало выходного списка (а не в конец выходного множества, как было в программном примере 3.7), элементы с большими ключами оттесняются к концу выходного списка и последний, таким образом, оказывается отсортированным по возрастанию ключей. Во-вторых, при поиске во входном списке сохраняется не только адрес найденного элемента в списке, но и адрес предшествующего ему в списке эле- мента - это впоследствии облегчает исключение элемента из списка (вспомните пример 5.4). В-третьих, обратите внимание на то, что у нас не возникает никаких проблем с пропуском во входном списке тех элементов, которые уже выбраны - они просто исключены из входной структуры данных.
{==== Программный пример 5.9 ====}
{ Сортировка выборкой на 1-связном списке }
Function Sort(head : lptr) : lptr;
var newh, max, prev, pmax, cur : lptr;
begin newh:=nil; { выходной список - пустой }
while head<>nil do { цикл, пока не опустеет входной список }
begin max:=head; prev:=head; { нач.максимум - 1-й эл-т }
cur:=head^.next; { поиск максимума во входном списке }
while cur<>nil do begin
if cur^.key>max^.key then begin
{ запоминается адрес максимума и адрес предыдущего эл-та }
max:=cur; pmax:=prev;
end; prev:=cur; cur:=cur^.next; { движение по списку }
end; { исключение максимума из входного списка }
if max=head then head:=head^.next
else pmax^.next:=max^.next;
{ вставка в начало выходного списка }
max^.next:=newh; newh:=max;
end; Sort:=newh;
end;
В программном примере 5.10 - иллюстрации сортировки вставками - из входного списка выбирается (и исключается) первый элемент и вставляется в выходной список "на свое место" в соответствии со значениями ключей. Сортировка включением на векторной структуре в примере 3.11 требовала большого числа перемещений элементов в памяти. Обратите внимание на то, что в двух последних примерах пересылок данных не происходит, все записи таблиц остаются на своих местах в памяти, меняются только связи между ними - указатели.
{==== Программный пример 5.10 ====}
{ Сортировка вставками на 1-связном списке }
type data = integer;
Function Sort(head : lptr) : lptr;
var newh, cur, sel : lptr;
begin
newh:=nil; { выходной список - пустой }
while head <> nil do begin { цикл, пока не опустеет входной список }
sel:=head; { эл-т, который переносится в выходной список }
head:=head^.next; { продвижение во входном списке }
if (newh=nil) or (sel^.key < newh^.key) then begin
{выходной список пустой или элемент меньше 1-го-вставка в начало}
sel^.next:=newh; newh:=sel; end
else begin { вставка в середину или в конец }
cur:=newh;
{ до конца выходного списка или пока ключ следующего эл-та не будет
больше вставляемого }
while (cur^.next <> nil) and (cur^.next^.key < sel^.key) do
cur:=cur^.next;
{ вставка в выходной список после эл-та cur }
sel^.next:=cur^.next; cur^.next:=sel;
end; end; Sort:=newh;
end;
В программных системах, обрабатывающих объекты сложной структуры, могут решаться разные подзадачи, каждая из которых требует, возможно, обработки не всего множества объектов, а лишь какого-то его подмножества. Так, например, в автоматизированной системе учета лиц, пострадавших вследствие аварии на ЧАЭС, каждая запись об одном пострадавшем содержит более 50 полей в своей информационной части. Решаемые же автоматизированной системой задачи могут потребовать выборки, например:
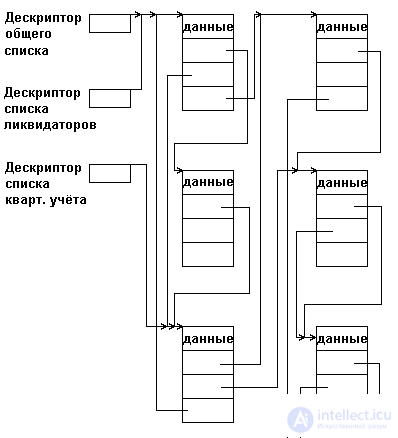
Рис.5.11. Пример мультисписка
Для того, чтобы при выборке каждого подмножества не выполнять полный просмотр с отсеиванием записей, к требуемому подмножеству не относящихся, в каждую запись включаются дополнительные поля ссылок, каждое из которых связывает в линейный список элементы соответствующего подмножества. В результате получается многосвязный список или мультисписок, каждый элемент которого может входить одновременно в несколько односвязных списков. Пример такого мультисписка для названной нами автоматизированной системы показан на рис.5.11.
К достоинствам мультисписков помимо экономии памяти (при множестве списков информационная часть существует в единственном экземпляре) следует отнести также целостность данных - в том смысле, что все подзадачи работают с одной и той же версией информационной части и изменения в данных, сделанные одной подзадачей немедленно становятся доступными для другой подзадачи.
Каждая подзадача работает со своим подмножеством как с линейным списком, используя для этого определенное поле связок. Специфика мультисписка проявляется только в операции исключения элемента из списка. Исключение элемента из какого-либо одного списка еще не означает необходимости удаления элемента из памяти, так как элемент может оставаться в составе других списков. Память должна освобождаться только в том случае, когда элемент уже не входит ни в один из частных списков мультисписка. Обычно задача удаления упрощается тем, что один из частных списков является главным - в него обязательно входят все имеющиеся элементы. Тогда исключение элемента из любого неглавного списка состоит только в переопределении указателей, но не в освобождении памяти. Исключение же из главного списка требует не только освобождения памяти, но и переопределения указателей как в главном списке, так и во всех неглавных списках, в которые удаляемый элемент входил.
5.4.1. Основные понятия
Нелинейным разветвленным списком является список, элементами которого могут быть тоже списки. В разделе 5.2 мы рассмотрели двухсвязные линейные списки. Если один из указателей каждого элемента списка задает порядок обратный к порядку, устанавливаемому другим указателем, то такой двусвязный список будет линейным. Если же один из указателей задает порядок произвольного вида, не являющийся обратным по отношению к порядку, устанавливаемому другим указателем, то такой список будет нелинейным.
В обработке нелинейный список определяется как любая последовательность атомов и списков (подсписков), где в качестве атома берется любой объект, который при обработке отличается от списка тем, что он структурно неделим.
Если мы заключим списки в круглые скобки, а элементы списков разделим запятыми, то в качестве списков можно рассматривать такие последовательности:
(a,(b,c,d),e,(f,g))
( )
((a))
The first list contains four elements: atom a, list (b, c, d) (containing in turn atoms b, c, d), atom e and list (f, g), whose elements are atoms f and g. The second list does not contain elements, however the zero list, in accordance with our definition, is a valid list. The third list consists of one element: list (a), which in turn contains atom a.
Another presentation method, often used to illustrate lists, is graphical diagrams, similar to the presentation method used to depict linear lists. Each item in the list is indicated by a rectangle; arrows or pointers indicate whether rectangles are elements of the same list or elements of a sublist. An example of such a presentation is given in Figure 5.12.
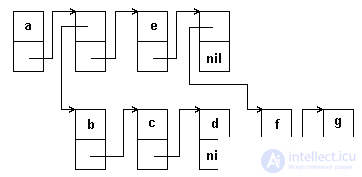
Fig.5.12. Schematic representation of an extensive list
Branched lists are described by three characteristics: order, depth and length.
Order. Above the elements of the list, a transitive relation is specified, determined by the sequence in which the elements appear inside the list. In the list (x, y, z), the atom x is preceded by y, and y is preceded by z. This implies that x precedes z. This list is not equivalent to the list (y, z, x). When lists are represented by graphical diagrams, the order is determined by horizontal arrows. Horizontal arrows are interpreted as follows: the element from which the arrow originates precedes the element to which it points.
Depth. This is the maximum level attributed to items within the list or within any sublist in the list. The element level is prescribed by the nesting of the sublists inside the list, i.e. the number of pairs of parentheses bordering the element. In the list shown in Figure 5.12), the elements a and e are at level 1, while the remaining elements - b, c, d, f and g have level 2. The depth of the input list is 2. When lists are represented by concept schemas Depths and levels are easier to understand if each number or atom number is attributed to an atomic or list node. The value of l for the element x, denoted as l (x), is the number of vertical arrows that must be traversed in order to reach a given element from the first element of the list. In Figure 5.12, l (a) = 0, l (b) = 1, etc. The depth of the list is the maximum level value among the levels of all atoms in the list.
Length is the number of elements of level 1 in the list. For example, the length of the list in Figure 5.12 is 3.
A typical example of an extensive list is the representation of the last algebraic expression in the form of a list. Algebraic expression can be represented as a sequence of elementary double operations of the form:
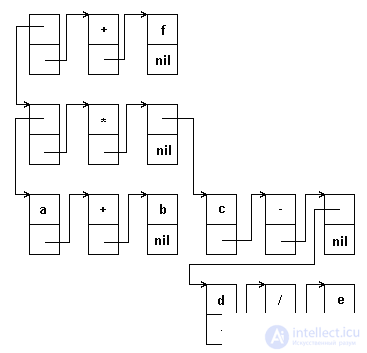
Fig.5.13. Schema of a list representing an algebraic expression
Expression:
(a + b) * (c- (d / e)) + f
will be calculated in the following order:
a + b
d / e
c- (d / e)
(a + b) * (cd / e)
(a + b) * (cd / e) + f
When representing an expression in the form of a branched list, each triple "operand-sign-operand" is represented as a list, and, as operands, can be either atoms — variables or constants, or sublists of the same kind. The bracket representation of our expression will be:
(((a, +, b), *, (c, -, (d, /, e)), +, f)
The depth of this list is 4, the length is 3.
5.4.2. Representation of list structures in memory.
In accordance with the schematic representation of branched lists, the typical structure of an element of such a list in memory should be the same as shown in Figure 5.14.

Fig.5.14. The structure of the element of the extensive list
The elements of the list can be of two types: atoms - containing data and nodes - containing pointers to sublists. In atoms, the down field of the list item is not used, and in nodes, the data field. Therefore, it is logical to combine these two fields into one, as shown in Figure 5.15.

Fig.5.15. The structure of the element of the extensive list
The type field contains the atom / node attribute, it can be 1-bit. This element format is convenient for lists whose atomic information occupies a small amount of memory. In this case, a small amount of memory is lost in the list items for which data fields are not required. In the more general case, atomic information requires a relatively large amount of memory. The most common format of the node structure in this situation is presented in Figure 5.16.

Fig. 5.16. The structure of the element of the extensive list
In this case, the down pointer points to the data or to a sublist. Since lists can be composed of data of different types, it is advisable to address with the pointer down not the data itself, but their descriptor, in which the data type, their length, etc. can be described. The very description of whether an object addressed by a data pointer is an atom or a node can also be in this descriptor. It is convenient to make the size of the data descriptor the same as the list item. In this case, the size of the type field can be extended, for example, to 1 byte, and this field can indicate not only the atom / sublist, but also the atomic data type, the next field in the data descriptor can be used to represent some other descriptive information, for example atom size. Fig.5.17 shows the presentation of elements of such a list format: (KOVAL (12,7,53), d). The first (top) line in the figure represents the elements of the list, the second - the elements of the sublist, the third - the data descriptors, the fourth - the data itself. In the type field of each element we used codes: n is a node, S is an atom, type STRING, I is an atom, type INTEGER, C is an atom, type CHAR.
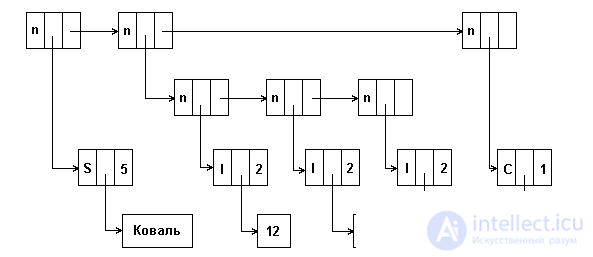
Fig.5.17. An example of a list of items in one format
5.4.3. List processing operations
The basic operations when processing lists are operations (functions): car, cdr, cons and atom.
The car operation takes a list as an argument (a pointer to the beginning of the list). Its return value is the first element of this list (pointer to the first element). For example:
The cdr operation also takes a list as an argument. Its return value is the rest of the list — a pointer to the list after removing the first item from it. For example:
The cons operation has two arguments: a pointer to a list item and a pointer to a list. The operation includes the argument element at the beginning of the list argument and returns a pointer to the resulting list. For example:
The atom operation performs a list item type check. It should return a boolean value: true - if its argument is an atom or false - if its argument is a sublist.
Programmatic example 5.11 shows the implementation of the described operations as functions of the PASCAL language. The structure of the element of the list processed by the functions of this module is defined in it as the litem type and fully corresponds to Fig.5.16. In addition to the described operations, the module also defines the memory allocation functions for the data descriptor - NewAtom and for the list item - NewNode. The implementation of operations is so simple that it does not require additional explanations.
{==== Software Example 5.11 ====}
{Elementary operations for working with lists}
Unit ListWork;
Interface
type lpt = ^ litem; {pointer to list item}
litem = record
typeflg: char; {Char (0) - node, otherwise - type code}
down: pointer; {pointer to data or sublist}
next: lpt; {pointer at current level}
end;
Function NewAtom (d: pointer; t: char): lpt;
Function NewNode (d: lpt): lpt;
Function Atom (l: lpt): boolean;
Function Cdr (l: lpt): lpt;
Function Car (l: lpt): lpt;
Function Cons (l1, l: lpt): lpt;
Function Append (l1, l: lpt): lpt;
Implementation
{*** creating a handle for an atom}
Function NewAtom (d: pointer; t: char): lpt;
var l: lpt;
begin New (l);
l ^ .typeflg: = t; {atom data type}
l ^ .down: = d; {data pointer}
l ^ .next: = nil; NewAtom: = l;
end;
{*** create list item for sublist}
Function NewNode (d: lpt): lpt;
var l: lpt;
begin
New (l);
l ^ .typeflg: = Chr (0); {sign of sub-list}
l ^ .down: = d; {pointer to start of sublist}
l ^ .next: = nil;
NewNode: = l;
end;
{*** list item check: true - atom, false - sublist}
Function Atom (l: lpt): boolean;
begin {type field check}
if l ^ .typeflg = Chr (0) then Atom: = false
else Atom: = true;
end;
Function Car (l: lpt): lpt; {selection of the 1st element from the list}
begin Car: = l ^ .down; {sample - pointer down} end;
Function Cdr (l: lpt): lpt; {excluding the 1st item from the list}
begin Cdr: = l ^ .next; {sample - pointer to the right} end;
{*** add an item to the top of the list}
Function Cons (l1, l: lpt): lpt;
var l2: lpt;
begin l2: = NewNode (l1); {list item to add}
l2 ^ .next: = l; {to the top of the list}
Cons: = l2; {returns the new beginning of the list}
end;
{*** add item to end of list}
Function Append (l1, l: lpt): lpt;
var l2, l3: lpt;
begin
l2: = NewNode (l1); {list item to add}
{if the list is empty - it will consist of one e-ta}
if l = nil then Append: = l2
else begin {exit to the last list item}
l3: = l; while l3 ^ .next <> nil do l3: = l3 ^ .next;
l3 ^ .next: = l2; {connect new e-ta to last}
Append: = l; {function returns the same pointer}
end; end;
End.
In Example 5.11, the Append function is turned on in the basic operations module - adding an element to the end of the list. In fact, this operation is not basic; it can be implemented using the described basic operations without reference to the internal structure of the list element, although, of course, such an implementation will be less fast. Software example 5.12 shows the implementation of several simple list processing functions that can be useful in solving a wide range of tasks. The functions of this module, however, do not use the internal structure of the list item.
{==== Software Example 5.12 ====}
{Secondary list processing functions}
Unit ListW1;
Interface
uses listwork;
Function Append (x, l: lpt): lpt;
Function ListRev (l, q: lpt): lpt;
Function FlatList (l, q: lpt): lpt;
Function InsList (x, l: lpt; m: integer): lpt;
Function DelList (l: lpt; m: integer): lpt;
Function ExchngList (l: lpt; m: integer): lpt;
Implementation
{*** add new item x to the end of list l}
Function Append (x, l: lpt): lpt;
begin
{if the list is empty - add x to the beginning of the empty list}
if l = nil then Append: = cons (x, l)
{if the list is non-empty
- take the same list without the 1st e-ta - cdr (l);
- add to its end al-x;
- add the first list to the beginning}
else Append: = cons (car (l), Append (x, cdr (l)));
end; {Function Append}
{*** Reverse list l; list q - resulting, at first
call it must be empty}
Function ListRev (l, q: lpt): lpt;
begin
{if input list is exhausted, return output list}
if l = nil then ListRev: = q
{otherwise: - add the 1st e-mail entry in the list to the beginning of the exit list,
- to reverse, having in. list without 1st e-ta, and out. List
- with added email}
else ListRev: = ListRev (cdr (l), cons (car (l), q));
end; {Function ListRev}
{*** Transformation of a branched list l into a linear one; q list
- resulting, at the first call it must be empty}
Function FlatList (l, q: lpt): lpt;
begin
{if input list is exhausted, return output list}
if l = nil then FlatList: = q
else
{if 1st el in. list - atom, then
- make the "flat" part of the input. list without 1st e-ta;
- add the 1st e-mail to its beginning}
if atom (car (l)) then
FlatList: = cons (car (l), FlatList (cdr (l), q))
{if 1st el in. list - sublist, then
- make the "flat" part of the entry list without the 1st e-ta;
- make a "flat" sublist of the 1st e-ta}
else FlatList: = FlatList (car (l), FlatList (cdr (l), q));
end; {Function FlatList}
{*** inserts into the list l of the element x in the place with the number m
(hereinafter, the numbering of emails in the list starts from 0)}
Function InsList (x, l: lpt; m: integer): lpt;
begin
{if m = 0, email is inserted at the top of the list}
if m = 0 then InsList: = cons (x, l)
{if the list is empty, it remains empty}
else if l = nil then InsList: = nil
{- insert the unit x in place of m-1 in the list without the 1st unit;
- insert the 1st el-t in the beginning of the received list}
else InsList: = cons (car (l), InsList (x, cdr (l), m-1));
end; {Function InsList}
{*** deletion from the list l at the place with the number m}
Function DelList (l: lpt; m: integer): lpt;
begin
{if the list is empty, it remains empty}
if l
продолжение следует...
Часть 1 5. DYNAMIC STRUCTURES OF DATA. RELATED LISTS
Часть 2 5.5. Язык программирования LISP - 5. DYNAMIC STRUCTURES OF DATA.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.