Lecture
Objective: to explore and explore search methods using the tree. The task of the work: to master the skills of writing programs for searching with the help of a binary tree in the PASCAL programming language. Operating procedure :
Brief theoryRemoving a tree node should not disrupt the orderliness of the tree. When deleting the following options for the location of nodes:
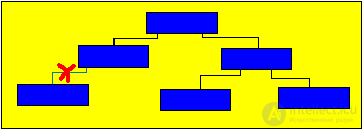
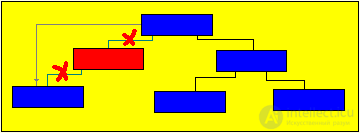
In this case, you need to find a suitable link of the subtree, which could be inserted in place of the deleted, and this suitable link should simply move. Such a link always exists: - this is the rightmost element of the left subtree (to reach this link, you must go to the next vertex on the left branch and then go to the next vertices only on the right branch until the next link is nil); - this is the leftmost element of the right subtree (to reach this link, you must go to the next vertex on the right branch and then go to the next vertices only on the left branch until the next such link is nil). Obviously, such suitable links may have no more than one branch. AlgorithmConsider an algorithm in which, instead of the node being deleted, the leftmost node of the right subtree is put. Remove the node with the number 150, then in its place will be the element at number 152, because it is the leftmost of the right subtree. We introduce the following notation: P - working pointer Q - pointer lagging behind P by one step V - pointer to the element that will replace the node to be deleted. T - pointer, one step behind V S - pointer, ahead of V by one step 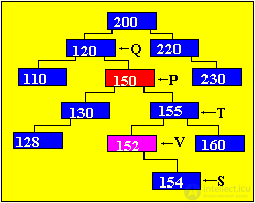 Sample program to remove elements of a binary tree (Pseudocode) Q = nil P = Tree While (P <> nil) and (K (P) <> key) do {find the node with the desired key} If key <k (p) then = "" p = "Left (P) <br"> Else P = Right (P) Endif Endwhile If P = nil then "Key not found" {check if there is no such item} Return {exit} Endif If Left (P) = nil then V = Right (P) {if the left link is nil Else If Right (P) = nil then V = Left (P) Else GetNode (P) T = p V = Right (P) S = Left (V) While S <> nil {search itself} T = V {left el-nta} V = S {right subtree} S = Left (V) Endwhile If T <> P then "V is not a son" Left (T) = Right (V) Right (V) = Right (P) Endif Left (V) = Left (P) If Q = nil then "p - root" Tree = V Return Endif If P = Left (Q) then Left (Q) = V Else Right (Q) = V Endif Endif Endif FreeNode (P) Return Illustration of the process of removing node 150, in accordance with the above algorithm (in red, new links in the tree are highlighted). 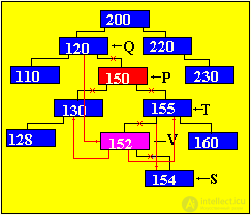 The final version of the tree after removal 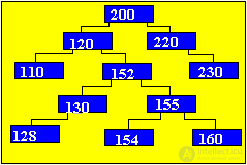 |
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.