Laboratory work number 6. "SORTING BY DIRECT INCLUSION METHOD"

Objective: to investigate and study the methods of sorting by inclusion.


The task of the work: to master the skills of writing programs for sorting by direct inclusion in the programming language PASCAL.


Operating procedure :

• 
  study the description of the laboratory work;

• 
  according to the task given by the teacher, to develop an algorithm for the program for solving the problem;

• 
  write a program in PASCAL;

• 
  debug the program;

• 
  to solve a task;

• 
  issue a report.

Brief theory

When processing data in a computer, it is important to know both the information field of the element and its placement in the memory of the machine. For these purposes sorting is used. So, sorting is the location of data in memory in a regular form by their keys. Regularity is considered as increasing the key value from the beginning to the end in the array.

There are the following types of sorts:

• 
  internal sorting is the sorting that takes place in the memory of the machine

• 
  external sorting - sorting in external memory.

If the sorted records occupy a large amount of memory, then their movement is expensive. In order to reduce them, the sorting is performed in the table of key addresses, the permutation of pointers is performed, i.e. the array itself does not move. This is a method to sort the address table.

When sorting can meet the same keys. In this case, when sorting, it is desirable to arrange after sorting the same keys in the same location as in the source file. This is a stable sort.

The sorting efficiency can be viewed from several criteria:

• 
  time spent on sorting

• 
  amount of RAM required for sorting

• 
  time spent by a programmer to write a program

Consider the second criterion in more detail: we can calculate the number of comparisons when performing sorting or the number of movements.

Suppose that the number of comparisons is determined by the formula:

C = 0.01n ² + 10n

If n <1000, then the second term is greater.

If n> 1000, then the first term is greater.

That is, for small n the order of comparison is equal, and for large n it is equal to n.

The following sorting methods are distinguished:

• 
  strict (direct) methods

• 
  improved methods

Consider the advantages of direct methods:

1. The programs of these methods are easy to understand, and they are short. Recall that the programs themselves also take up memory.

2. Direct methods are particularly convenient for explaining the characteristic features of the basic principles of most sorts.

3. Complicated methods require a small number of operations, but these operations are usually more complex themselves, and therefore for sufficiently small n the direct methods turn out to be faster, although for large n they, of course, should not be used.


Sorting methods "in the same place" can be divided according to their defining principles into 3 categories:

1. Sorting by means of inclusion (by insertion)

2. Sorting by selection (by selection)

3. Sorting using exchanges (by exchange)


Sort by direct inclusion


This method is widely used when playing cards. The elements (maps) are mentally divided into the already “ready” sequence a (1), ..., a (i-1) and the initial sequence. At each step, starting with i = 2 and increasing i each time by one, the i-th element is extracted from the initial sequence and transferred to the finished sequence, and it is inserted into the right place.

Algorithm

Direct methods include direct selection.

Consider the entire array row and select an element smaller or larger than element a (i), determine its place in the array - k, and then swap element a (i) and element a (k).

for i = 1 to n - 1

x = a (i)

k = i

for j = i + 1 to n

if x> a (j) then

k = j

x = a (k)

endif

next j

a (k) = a (i)

a (i) = x

next i

return

for i: = 1 to n - 1 do

begin

x: = a [i];

k: = i;

for j: = i + 1 to n do

if x> a [j] then

begin

k: = j;

x: = a [k];

end;

a [k]: = a [i];

a [i]: = x;

end;


Efficiency of the algorithm:

• 
  Number of comparisons

• 
  Number of moves when array is ordered

• 
  Number of moves when the array is back sorted

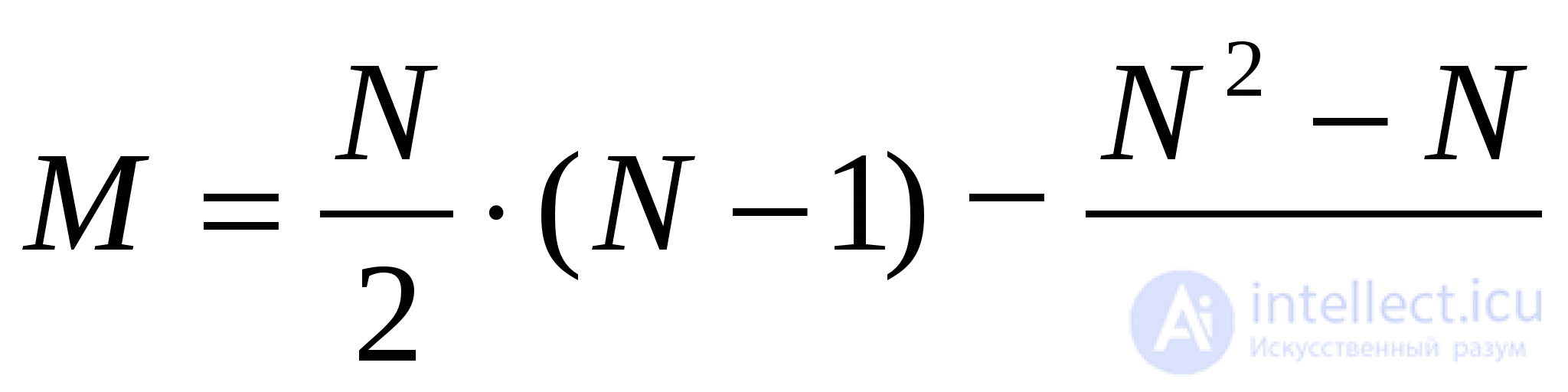
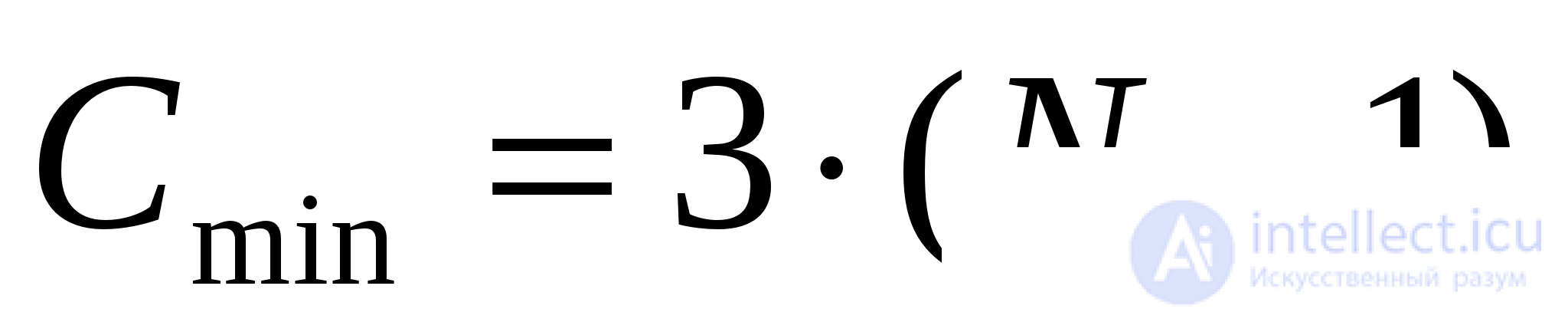
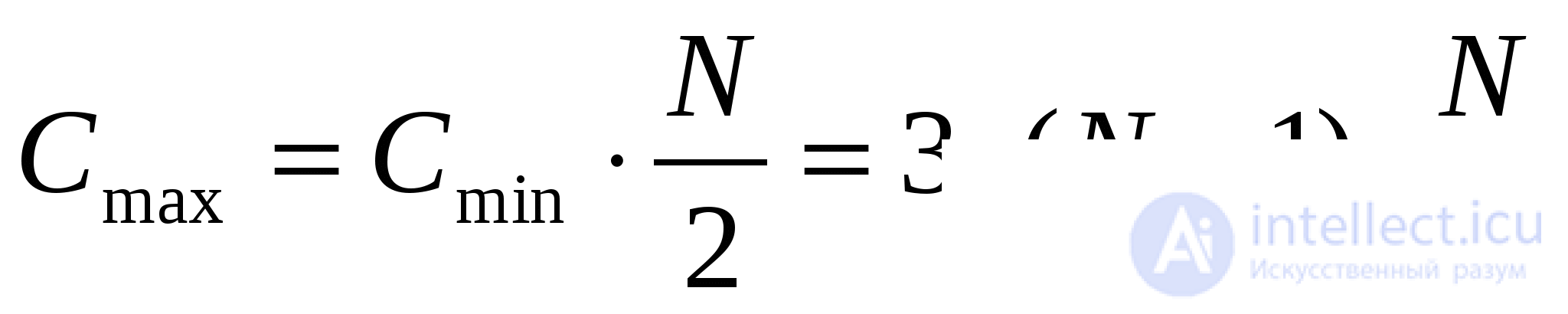
In the worst case, sorting by direct choice gives the order of n ² , as for the number of comparisons, and for the number of displacements.

Tasks

Create a group of N students. Enter them: last name, first name, year of birth, assessment of subjects: p. And al., Higher. mathematics, physics, programming, the total score of the session; Develop a program using the method of "direct selection", which would carry out the sorting (according to option):

1. Names of students alphabetically.

2. Names of students alphabetically in reverse order.

3. Seniority students (starting from the oldest).

4. Seniority students (starting from the youngest).

5. Students on a general score (ascending).

6. Students by total score (descending).

7. Students according to the results of the 1st exam (ascending).

8. Students according to the results of the 2nd exam (descending).

9. Students according to the results of the 3rd exam (ascending).

10. Students according to the results of the 4th exam (descending).

11. Names in alphabetical order.

12. Names in reverse alphabetical order.