5.8 Inserted search (with inclusion) 5.9 Deleted search

5.8 Search with insert (with inclusion)

To insert an element into the tree, you first need to search the tree for a given key. If there is such a key, the program is terminated; if not, an insertion occurs.

To include a new entry in the tree, first of all you need to find the node to which you can attach a new element. The algorithm for finding the desired node is the same as when searching for a node with a given key. However, the search procedure cannot be used directly, because after its completion the node from which the NIL link was selected (search = nil) does not fix.

We modify the description of the search procedure so that, as its side effect, there is a link to the node where the specified key was found (in case of a successful search), or a link to the node after which processing the search stops (in case of unsuccessful search).

Pseudocode: P = tree Q = nil Whlie p <> nil do q = p if key = k (p) then search = p return endif if key <k (p) then p = left (p) else p = right (p) endif endwhile v = maketree (key, rec) if q = nil then tree = v else if key <k (q) then left (q) = v else right (q) = v endif endif search = v return

Pascal: p: = tree; q: = nil; whlie p <> nil do begin q: = p; if key = p ^ .k then begin search: = p; exit; end; if key <p ^ .k then p: = p ^ .left else p: = p ^ .right; end; v: = maketree (key, rec) if q = nil then tree: = v else if key <q ^ .k then q ^ .left: = v else q ^ .right: = v; search: = v;

5.9 Search with delete

Deleting a node should not disrupt the ordering of the tree. There are three options:

1) The found node is a leaf. Then he just deleted everything.

2) The found node has only one son. Then the son moves to the father's place.

3) The removed node has two sons. In this case, you need to find a suitable link of the subtree, which could be inserted in place of the deleted one. Such a link always exists:

- this is either the rightmost element of the left subtree (to reach this link, you must go to the next vertex on the left branch, and then go to the next vertices only on the right branch until the next link is equal to NIL.

- either the leftmost element of the right subtree (to reach this link, you must go to the next vertex on the right branch, and then go to the next vertices only on the left branch until the next link is equal to NIL

The predecessor of the deleted node is the right-most node of the left subtree (for 12-11). The successor is the leftmost node of the right subtree (for 12–13).

We will develop an algorithm for the successor (Fig.5.9).

p - working pointer;

q - one step behind p;

v - indicates the receiver of the node to be deleted;

t - one step behind v;

s - one step ahead of v (indicates left son or empty space).





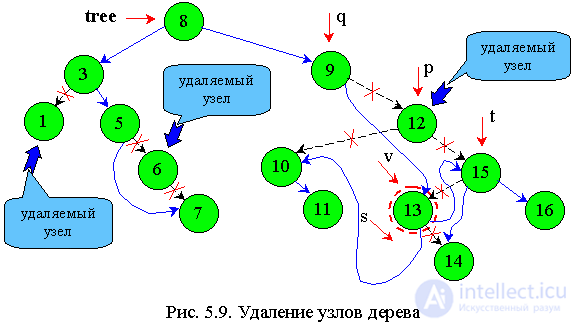
The node 13 should ultimately indicate v, and the pointer s should indicate empty space (as shown in Figure 5.9).

Pseudocode: q = nil p = tree while (p <> nil) and (k (p) <> key) do q = p if key <k (p) then p = left (p) else p = right (p) endif endwhile if p = nil then 'Key not found' return endif if left (p) = nil then v = right (p) else if right (p) = nil then v = left (p) else 'U nod (p) - two sons'   'We introduce two pointers (t is one step behind v by', s is ahead) t = p v = right (p) s = left (v) while s <> nil do t = v v = s s = left (v) endwhile if t <> p then 'v is not the son of p' left (t) = right (v) right (v) = right (p) endif left (v) = left (p) endif endif if q = nil then 'p - root' tree = v else if p = left (q) then left (q) = v else right (q) = v endif endif freenode (p) return

Pascal: q: = nil; p: = tree; while (p <> nil) and (p ^ .k <> key) do begin q: = p; if key <p ^ .k then p: = p ^ .left else p: = p ^ .right; end; if p = nil then WriteLn ('Key not found'); exit; end; if p ^ .left = nil then v: = p ^ .right else if p ^ .right = nil then v: = p ^ .left else begin {We introduce two pointers (t is one step behind v, s is ahead)} t: = p; v: = p ^ .right; s: = v ^ .left; while s <> nil do begin t: = v; v: = s; s: = v ^ .left; end; if t <> p then begin WriteLn ('v is not a son of p'); t ^ .left: = v ^ .right; v ^ .right: = p ^ .right; end; v ^ .left: = p ^ .left; end; end; if p = q ^ .left then q ^ .left: = v else q ^ .right: = v; end; dispose (p); end;

test questions

1. 
   What is the purpose of the search?
2. 
   What is a unique key?
3. 
   What operation is performed in the absence of a given key in the list?
4. 
   What is the difference between sequential and index-sequential search?
5. 
   Which one is more effective and why?
6. 
   What methods of reordering the table do you know?
7. 
   The main differences between the permutation method and the transposition method.
8. 
   Where will they work faster, in an array or list?
9. 
   What lists do they work in, ordered or not?
10. 
    What is the essence of a binary search?
11. 
    How can I get around a binary tree?
12. 
    Is it possible to apply binary search to arrays?
13. 
    If you delete a root in a non-empty binary tree, which element will take its place?