3. Dynamic data structures

So far, we have considered only static program objects. However, the use of only static objects in programming can cause certain difficulties, especially from the point of view of obtaining an efficient machine program. The fact is that sometimes we do not know in advance not only the size of the value of a program object, but also whether this object will exist or not. Such software objects, which appear already in the process of program execution or the size of values ​​of which is determined during program execution, are called dynamic objects.

Dynamic data structures have 2 features:

1. 
   The number of elements in the structure is not determined in advance.
2. 
   Elements of dynamic structures do not have a rigid linear order. They can be scattered in memory.

In order to link the elements of dynamic structures among themselves, the elements in addition to the information fields include pointer fields (Fig. 3.1) (bundles with other elements of the structure).





P ₁ and P ₂ are pointers containing the addresses of the elements with which they are associated. Pointers contain the slot number.

3.1 Linked Lists

The most common dynamic structures are linked lists. From the point of view of logical representation distinguish linear and nonlinear lists.

In linear lists, links are strictly ordered: the pointer of the previous element contains the address of the next element or vice versa.

Linear lists are simply linked and doubly linked lists. For nonlinear - multiply.

A list item is generally a record field and one or more pointers.

3.1.1 Singly linked lists

The element of a simply linked list contains two fields (Fig. 3.2): an information field (INFO) and a pointer field (PTR).





The peculiarity of the pointer is that it gives only the address of the subsequent element of the list. The index field of the last item in the list is empty (NIL). LST - pointer to the beginning of the list. The list may be empty, then LST will be equal to NIL.

Access to the list item is only from its beginning, that is, there is no feedback in this list.

3.1.2 Ring-related list

A simply-linked ring list is obtained from a simple simply-connected list by assigning to the pointer the last element of the list the value of the pointer to the beginning of the list (Figure 3.3).



The simplest operations performed on singly-linked lists

1. 
   Insert at the beginning of a single-linked list.

It is necessary to insert an element with the information field D at the beginning of a single-linked list. To do this, an empty element must be generated (P = GetNode). Assign the value of D (INFO (P) = D) to the information field of this element, assign the pointer value to the beginning of the list (Ptr (P) = Lst) to the pointer value of this element, assign the value of the pointer P (Lst = P) to the value of the pointer of the beginning of the list.

Pascal implementation:

type

PNode = ^ TNode;

TNode = record

Info: Integer; {type of list items - can be any}

Next: PNode;

end;

var

Lst: PNode; {pointer to the beginning of the list}

P: PNode;

Insert at the beginning

New (P); {create new item}

P ^ .Info: = D;

P ^ .Next: = Lst; {P indicates the beginning of the list, but Lst does not indicate P - new beginning}

Lst: = P; {Lst points to the new beginning of the list}

2. 
   Remove an item from the beginning of a single-linked list.

It is necessary to delete the first element of the list, but remember the information contained in the Info field of this element. To do this, enter the pointer P, which will point to the element to be deleted (P = Lst). In the variable X, enter the value of the Info information field of the element to be deleted (X = Info (P)). The value of the pointer at the beginning of the list is assigned to the value of the pointer following the element to be deleted (Lst = Ptr (P)). Remove the item (FreeNode (P)).

Implementation in Pascal:

Remove from start

P: = Lst;

X: = P ^ .Info;

Lst: = P ^ .Next;

Dispose (P); {Deletes an element from dynamic memory}

3.1.3 Twofold list

The use of unidirectional lists for solving a number of tasks can cause certain difficulties. The fact is that a unidirectional list can only move in one direction, from the title link to the last link in the list. Meanwhile, it is often necessary to perform any processing of elements that precede an element with a given property. However, after finding an element with this property in a simply-connected list, we are not able to get reasonably convenient and quick access to the previous elements — to achieve this goal, we will have to complicate the algorithm, which is inconvenient and irrational.

To eliminate this inconvenience, we will add one more field to each link of the list, the value of which will be a link to the previous link of the list. A dynamic structure consisting of elements of this type is called a bidirectional or doubly linked list.

A doubly linked list is characterized by the fact that any item has two pointers. One points to the previous element (reverse), the other points to the next element (direct) (Fig. 3.4).




In fact, a doubly linked list is two simply connected lists with the same elements, written in the opposite sequence.

3.1.4 Ring doubly linked list

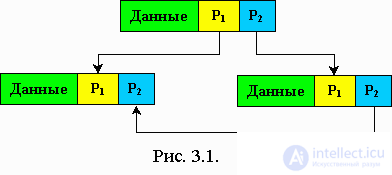
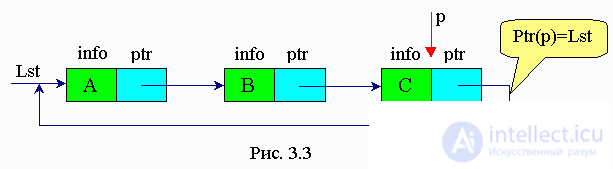
In programming, doubly-linked lists are often summarized as follows: as the value of the Rptr field of the last link, they take a link to the title link, and as the value of the Lptr field of the title link, the link to the last link. The list closes into a kind of ring: by following the links, you can go from the last link to the title link and vice versa.




ABOUT Operations over doubly linked lists:

- create a list item;

- Search for an item in the list;

- insert an item in the specified place in the list;

- removal of the specified item from the list.

3.2 Implementing Stacks Using Single-Linked Lists

Any single-linked list can be viewed as a stack. However, the list has an advantage over the stack in the form of a one-dimensional array, since its size has not been predefined.


Stack operations applicable to lists

one). To add an element to the stack, it is necessary in the algorithm to replace the pointer Lst with the pointer Stack (operation Push (S, X)).


P = GetNode

Info (P) = X

Ptr (P) = Stack

Stack = P

2. 
   Check stack for void (Empty (S))

If Stack = Nil then Print “The stack is empty”

Stop

3. 
   Fetch item from stack (POP (S))

P = Stack

X = Info (P)

Stack = Ptr (P)

FreeNode (P)


Implementation in Pascal:

Stack


Instead of the Lst pointer, the Stack pointer is used.

Push procedure (S, X)


procedure Push (var Stack: PNode; X: Integer);

var

P: PNode;

begin

New (P);

P ^ .Info: = X;

P ^ .Next: = Stack;

Stack: = P;

end;


Check for emptiness (Empty)


function Empty (Stack: PNode): Boolean;

begin

If Stack = nil then Empty: = True Else Empty: = False;

end;


Pop procedure


procedure Pop (var X: Integer; var Stack: PNode);

var

P: PNode;

begin

P: = Stack;

X: = P ^ .Info;

Stack: = P ^ .Next;

Dispose (P);

end;


Queue operations that apply to lists.


A pointer to the beginning of the list is taken as the pointer to the beginning of the queue F, and a pointer R that points to the last element of the list is taken as the pointer to the end of the queue.

1. 
   The operation of removal from the queue (Remove (Q, X)).

The delete operation from the queue must pass from its beginning.

P = F

F = Ptr (P)

X = Info (P)

FreeNode (P)

2. 
   Check the queue for emptiness. (Empty (Q))

If F = Nil then Print “The queue is empty”

Stop

3. 
   The operation of inserting into the queue. (Insert (Q, X))

The insert operation in the queue should be carried out to its end.

P = GetNode

Info (P) = X

Ptr (P) = Nil

Ptr (R) = P

R = P


Implementation in Pascal:

procedure Remove (var X: Integer; Fr: PNode);

var

P: PNode;

begin

New (P);

P: = Fr;

X: = P ^ .Info;

Fr: = P ^ .Next;

Dispose (P);

end;


function Empty (Fr: PNode): Boolean;

begin

If Fr = nil then Empty: = True Else Empty: = False;

end;


procedure Insert (X: Insert; var Re: PNode);

var

P: PNode;

begin

New (P);

P ^ .Info: = X;

P ^ .Next: = nil;

Re ^ .Next: = P;

end;

3.3 Organization of operations Getnode, Freenode and disposal of released elements

For more efficient use of computer memory (to eliminate garbage , that is, unused items) when working with lists it creates a free list that has the same field format as functional lists.

If the functional lists have a different format, then it is necessary to create a free list of each functional list.

The number of items in the free list must be determined by the task that the program solves. As a rule, a free list is created in the memory of the machine as a stack. In this case, the creation ( GetNode ) of a new element is equivalent to fetching an element of a free stack, and the FreeNode operation is adding a free element to a free stack.

Suppose we need to create an empty list of the type of stack (Fig. 3.6) with a pointer to the beginning of the list - AVAIL. We will develop procedures that allow us to create an empty list item and free an item from the list.

3.3.1 GetNode operation

We will develop a procedure that will create an empty list item with a pointer R.

To implement the GetNode operation, you need to assign the pointer value of the beginning of the free list to the pointer of the generated element, and move the pointer to the next element.


P = Avail

Avail = Ptr (avail)


Before this, you need to check whether there are items in the list. The void of a free list (Avail = Nil) is equivalent to the overflow of a functional list.


If Avail = Nil then Print “Overflow” Stop

Else

P = Avail

Avail = Ptr (avail)

Endif

3.3.2 FreeNode operation

When the Nod (P) element is freed from the functional list by the FreeNode (P) operation, it is entered into the free list.

Ptr (P) = avail

Avail = P

3.3.3 Disposal of freed items on multiply linked lists

The standard operations of returning a vacated list item to a pool of free elements do not always have an effect if nonlinear multiply connected lists are used.

The first method of disposal is the counter method. The field of the counter which counts the number of links to this element is inserted into each element of the multiply linked list. When the element counter is in the zero state, and the element pointer fields are in the nil state, this element can be returned to the pool of free elements.

The second method is garbage collection (marker method). If a connection is established with some element, then the one-bit element field (marker) is set to “1”, otherwise - to “0”. The overflow signal looks for elements whose marker is set to zero, i.e., the garbage collection program is turned on, which scans all allocated memory and returns all elements not marked with a marker to the free list.

3.4 Singly-linked list as an independent data structure

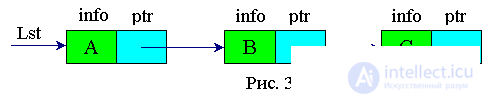
A single-linked list can be viewed only sequentially, starting from the head (from the beginning) of the list. If you need to view the previous item, then you need to go back to the top of the list. This is a disadvantage of simply linked lists compared to static structures like an array. The list structure shows its advantages when the number of elements in the list is large, and insertion or deletion must be made inside the list.

Example:

You must insert an element X between 5 and 6 elements into an existing array.





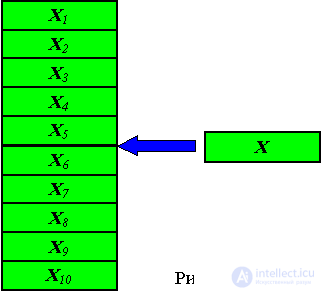
To perform this operation in the array, you need to “omit” all elements starting from X6 - increase their indices by one. As a result of insertion, we get the following array (fig. 3.7, 3.8):




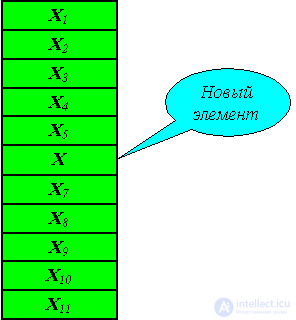
This procedure can take a very significant time. In contrast, in the linked list, the insert operation consists in changing the value of 2 pointers and generating a free element. Moreover, the time spent on this operation is constant and does not depend on the number of items in the list.

3.4.1 Inserting and retrieving items from the list

We define the element after which it is necessary to insert the element into the list. The insertion is done using the InsAfter procedure (Q, X), and the deletion is done DelAfter (Q, X).

At the same time, the working pointer P will point to the element after which it is necessary to insert or delete (Fig. 29).



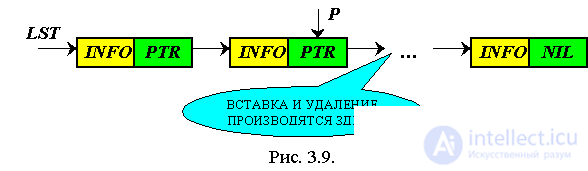
Example:

Let it be necessary to insert a new element with information field X after the element pointed to by the working pointer P.

For this:

one) You need to generate a new item.

Q = GetNode

2) Assign the value X to the information field of this element.

Info (Q) = X

3) Insert received item.

Ptr (Q) = Ptr (P)

Ptr (P) = Q

This is the InsAfter (Q, X) procedure.

Suppose you need to delete the list item that follows the item pointed to by the working pointer P.

For this:

1. 
   We assign the Q value of the pointer to the element to be deleted.

Q = Ptr (P)

2) In the variable X, save the value of the information field of the element to be deleted.

X = Info (Q)

3) Change the value of the pointer to the element to be deleted with the value of the pointer to the next element and delete it.

Ptr (P) = Ptr (Q)

FreeNode (Q)

This is the DelAfter (P, X) procedure.


In Pascal, the procedures described above will be as follows:

procedure InsAfter (var Q: PNode; X: Integer);

var

Q: PNode;

begin
New (Q);
Q ^ .Info: = X;
Q ^ .Next: = P ^ .Next;
P ^ .Next: = Q;

procedure DelAfter (var Q: PNode; var X: Integer);

var
Q: PNode;
begin
Q: = P ^ .Next;
P ^ .Next: = Q ^ .Next;
X: = Q ^ .Info;
Dispose (Q);
end;

3.4.2 Examples of typical list operations

Task 1.

It is required to view the list and delete elements whose information fields are equal to 4.

Let P - work pointer, at the beginning of the procedure P = Lst. We also introduce a pointer Q, which is one element behind P. When the pointer P finds an element, the latter will be deleted relative to the pointer Q as a subsequent element.

Q = Nil
P = Lst
While P <> Nil do
If Info (P) = 4 then
If Q = Nil then
Pop (lst)
FreeNode (P)
P = Lst
Else
DelAfter (Q, X)
Endif
Else
Q = P
P = Ptr (P)
Endif
Endwhile


Task 2.

Dan is ordered in ascending Info - list of fields. It is necessary to insert into this list an element with the value X, without disturbing the orderliness of the list.



Let X = 16. The initial condition: Q = Nil, P = Lst. The insertion of the element should occur between the 3rd and 4th elements (Fig.3.10).

Q = Nil
P = Lst
while (P <> Nil) and (X> Info (P)) do
Q = P
P = Ptr (P)
Endwhile
if Q = Nil then
Push (Lst, X)
Endif
InsAfter (Q, X)

Implementation of examples in Pascal:


Task 1:

Q: = nil;
P: = Lst;
While P <> nil do
If P ^ .Info = 4 then
begin
If Q = nil then
begin
Pop (Lst);
P: = Lst;
end
Else Delafter (Q, X);
End;
Else
begin
Q: = P;
P: = P ^ .Next;
end;
end;

Task 2:

Q: = nil;

P: = Lst;

While (P <> nil) and (X> P ^ .Info) do

begin

Q: = P;

P: = P ^ .Next;

end;

{This point is inserted}

If Q = nil then Push (Lst, X);

InsAfter (Q, X);

End;

3.4.3 Header Elements in Lists

To create a list with a header, an additional element is entered at the top of the list, which may contain information about the list (Fig. 3.11).





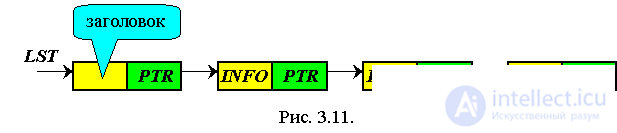
A dynamic variable is often placed in the list header, containing the number of elements in the list (not counting the title itself).

If the list is empty, then only the list header remains (Fig. 3.12).





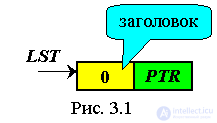
It is also convenient to enter the value of the end of list pointer in the header information field. Then, if the list is used as a queue, then Fr = Lst, and Re = Info (Lst).

The header information field can be used to store the working pointer when viewing the P = Info (Lst) list. That is, the header is a data structure descriptor.

3.5 Nonlinear related structures

A doubly linked list can be a non-linear data structure if the second pointers specify an arbitrary order of the elements (Fig. 3.13).





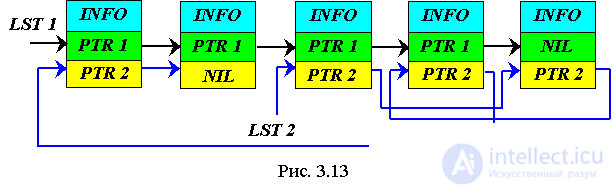
LST1 is a pointer to the beginning of the 1st list (oriented by pointer P1). It is linear and consists of 5 elements.

The 2nd list is formed from the same elements, but in an arbitrary sequence. The beginning of the 2nd list is the 3rd element, and the end of the 2nd element.

In the general case, the element of the list structure can contain as many pointers as it wishes, that is, it can indicate any number of elements.

There are 3 signs of differences in nonlinear structure:

1) Any element of the structure can refer to any number of other elements of the structure, that is, it can have any number of pointer fields.

2) Any number of other elements of this structure may refer to this structure element.

3) Links may have weight, that is, a hierarchy of links is implied.

Imagine that there is a discrete system, in the state graph of which nodes are states and edges are transitions from state to state (Fig. 3.14).



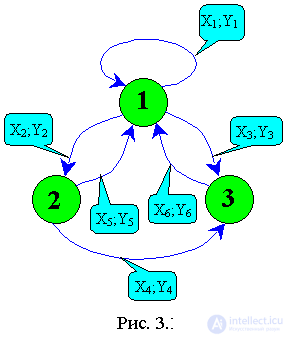
The input signal to the system is X. The reaction to the input signal is the generation of the output signal Y and the transition to the corresponding state.

The state graph of a discrete system can be represented as a doubly connected nonlinear list. In this case, information on the system states and edges must be recorded in the information fields. The pointers of the elements should form the logical edges of the system (Fig. 3.15).

To implement the above:

1) a list should be created that displays the state of the system (1, 2, 3);

2) lists should be created that reflect the transitions along edges from the corresponding states.





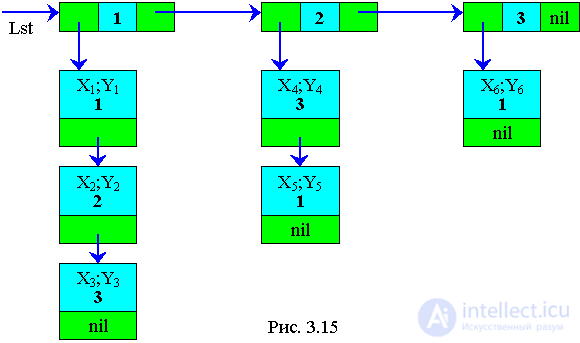
In general, when implementing a multiply-connected structure, a network is obtained.


test questions

1. What dynamic structures are known to you?
2. What is the distinctive feature of dynamic objects?
3. What type is presented for working with dynamic objects?
4. How are the elements in a dynamic structure?
5. What are the main features of a single-linked list ..
6. What is the difference between linear and ring lists?
7. Why were doubly linked lists introduced?
8. What is the difference in operations performed on singly-connected and doubly-linked lists?
9. Which list is more user-friendly, singular or biconnected?
10. What is a pointer?
11. What stack operations can be performed on lists?
12. What operations performed on the queue can be performed on lists?
13. Why is it possible to perform all these operations on lists?
14. What are the Getnode and Freenode operations for?
15. What recycling methods do you know?
16. List the headings in the lists.
17. Does the time taken to insert an element in a single-linked list depend on the number of elements in the list?
18. Where is the insertion and deletion process more efficiently, in a list or in an array?
19. How can I view a single-linked list?
20. What does AVAIL mean?
21. What is the disadvantage of simply linked lists compared to an array?
22. What structures are non-linear?
23. What are the signs of differences in nonlinear structures?
24. How can you create a nonlinear connected structure?
25. What is a state graph?