You get a bonus - 1 coin for daily activity. Now you have 1 coin

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Lecture



He has a lot of knowledge to study. It is a clear idea that they have been making it. In Java and also show the following operations:

  1. Inserting / Building a BST
  2. Finding maximum value node in BST
  3. Finding minimum value node in BST
  4. Inorder Traversal of BST
  5. Preorder Traversal of BST
  6. Postorder Traversal of BST

What is a Binary Search Tree (BST)?

It has been shown that it has been shown that it can be used in the field. Lets look at an example of a BST:

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

It is no longer a case for a child.

Building a Binary Search Tree (BST)

It is clear that in the Java system it’s possible to make it. The basic idea is that it is inserted. If there is a difference, it can be greater than It allows you to insert the value 64 in the above BST, lets you put it on the right place:

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Each node in the BST is by the java class below:

1 public class Node {
2 public int value;
3 public Node left;
4 public Node right;
5
6 public Node( int value) {
7 this .value = value;
8 }
9
10 }

Lets look for the above logic:

1 public class BinarySearchTree {
2 public Node root;
3
4 public void insert( int value){
5 Node node = new Node<>(value);
6
7 if ( root == null ) {
8 root = node;
9 return ;
10 }
11
12 insertRec(root, node);
13
14 }
15
16 private void insertRec(Node latestRoot, Node node){
17
18 if ( latestRoot.value > node.value){
19
20 if ( latestRoot.left == null ){
21 latestRoot.left = node;
22 return ;
23 }
24 else {
25 insertRec(latestRoot.left, node);
26 }
27 }
28 else {
29 if (latestRoot.right == null ){
30 latestRoot.right = node;
31 return ;
32 }
33 else {
34 insertRec(latestRoot.right, node);
35 }
36 }
37 }
38 }

Finding Maximum and Minimum Value in BST

If you have a note, it has the highest value. This is a sorted nature of the tree.

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Using the Binary Search Tree:

1 /**
2 * Returns the minimum value in the Binary Search Tree.
3 */
4 public int findMinimum(){
5 if ( root == null ){
6 return 0 ;
7 }
8 Node currNode = root;
9 while (currNode.left != null ){
10 currNode = currNode.left;
11 }
12 return currNode.value;
13 }
14
15 /**
16 * Returns the maximum value in the Binary Search Tree
17 */
18 public int findMaximum(){
19 if ( root == null ){
20 return 0 ;
21 }
22
23 Node currNode = root;
24 while (currNode.right != null ){
25 currNode = currNode.right;
26 }
27 return currNode.value;
28 }

Traversing the Binary Search Tree (BST)

This is the path to the bottom of the tree. If you want to go there, go ahead . The tree will be a recursive operation. It gives you the number of traversal techniques:

  1. Inorder traversal
  2. Preorder traversal
  3. Postorder traversal

Inorder traversal

It is a list of the rules of interest. It is a process of recursively.

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Applying the Inorder traversal for the give example we get: 3, 10, 17, 25, 30, 32, 38, 40, 50, 78, 78, 93.

1 /**
2 * Printing the contents of the tree in an inorder way.
3 */
4 public void printInorder(){
5 printInOrderRec(root);
6 System.out.println( "" );
7 }
8
9 /**
10 * Helper method to recursively print the contents in an inorder way
11 */
12 private void printInOrderRec(Node currRoot){
13 if ( currRoot == null ){
14 return ;
15 }
16 printInOrderRec(currRoot.left);
17 System.out.print(currRoot.value+ ", " );
18 printInOrderRec(currRoot.right);
19 }

Preorder traversal

It has been noted. It is a process of recursively.

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

We get: 40, 25, 10, 3, 17, 32, 30, 38, 78, 50, 78, 93.

1 /**
2 * Printing the contents of the tree in a Preorder way.
3 */
4 public void printPreorder() {
5 printPreOrderRec(root);
6 System.out.println( "" );
7 }
8
9 /**
10 * Helper method to recursively print the contents in a Preorder way
11 */
12 private void printPreOrderRec(Node currRoot) {
13 if (currRoot == null ) {
14 return ;
15 }
16 System.out.print(currRoot.value + ", " );
17 printPreOrderRec(currRoot.left);
18 printPreOrderRec(currRoot.right);
19 }

Postorder traversal

This is the first time it has been found. It is a process of recursively.

Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java

Applying the Postorder traversal for the give example we get: 3, 17, 10, 30, 38, 32, 25, 50, 93, 78, 78, 40.

1 /**
2 * Printing the contents of the tree in a Postorder way.
3 */
4 public void printPostorder() {
5 printPostOrderRec(root);
6 System.out.println( "" );
7 }
8
9 /**
10 * Helper method to recursively print the contents in a Postorder way
11 */
12 private void printPostOrderRec(Node currRoot) {
13 if (currRoot == null ) {
14 return ;
15 }
16 printPostOrderRec(currRoot.left);
17 printPostOrderRec(currRoot.right);
18 System.out.print(currRoot.value + ", " );
19
20 }

This is the complete code for the example, the order code, the order code, the order number, the order number, the order number, the order number and the order number:

view source
print?
1 /**
2 * Represents a node in the Binary Search Tree.
3 */
4 public class Node {
5 //The value present in the node.
6 public int value;
7
8 //The reference to the left subtree.
9 public Node left;
10
11 //The reference to the right subtree.
12 public Node right;
13
14 public Node( int value) {
15 this .value = value;
16 }
17
18 }
19
20 /**
21 * Represents the Binary Search Tree.
22 */
23 public class BinarySearchTree {
24
25 //Refrence for the root of the tree.
26 public Node root;
27
28 public BinarySearchTree insert( int value) {
29 Node node = new Node<>(value);
30
31 if (root == null ) {
32 root = node;
33 return this ;
34 }
35
36 insertRec(root, node);
37 return this ;
38 }
39
40 private void insertRec(Node latestRoot, Node node) {
41
42 if (latestRoot.value > node.value) {
43
44 if (latestRoot.left == null ) {
45 latestRoot.left = node;
46 return ;
47 } else {
48 insertRec(latestRoot.left, node);
49 }
50 } else {
51 if (latestRoot.right == null ) {
52 latestRoot.right = node;
53 return ;
54 } else {
55 insertRec(latestRoot.right, node);
56 }
57 }
58 }
59
60 /**
61 * Returns the minimum value in the Binary Search Tree.
62 */
63 public int findMinimum() {
64 if (root == null ) {
65 return 0 ;
66 }
67 Node currNode = root;
68 while (currNode.left != null ) {
69 currNode = currNode.left;
70 }
71 return currNode.value;
72 }
73
74 /**
75 * Returns the maximum value in the Binary Search Tree
76 */
77 public int findMaximum() {
78 if (root == null ) {
79 return 0 ;
80 }
81
82 Node currNode = root;
83 while (currNode.right != null ) {
84 currNode = currNode.right;
85 }
86 return currNode.value;
87 }
88
89 /**
90 * Printing the contents of the tree in an inorder way.
91 */
92 public void printInorder() {
93 printInOrderRec(root);
94 System.out.println( "" );
95 }
96
97 /**
98 * Helper method to recursively print the contents in an inorder way
99 */
100 private void printInOrderRec(Node currRoot) {
101 if (currRoot == null ) {
102 return ;
103 }
104 printInOrderRec(currRoot.left);
105 System.out.print(currRoot.value + ", " );
106 printInOrderRec(currRoot.right);
107 }
108
109 /**
110 * Printing the contents of the tree in a Preorder way.
111 */
112 public void printPreorder() {
113 printPreOrderRec(root);
114 System.out.println( "" );
115 }
116
117 /**
118 * Helper method to recursively print the contents in a Preorder way
119 */
120 private void printPreOrderRec(Node currRoot) {
121 if (currRoot == null ) {
122 return ;
123 }
124 System.out.print(currRoot.value + ", " );
125 printPreOrderRec(currRoot.left);
126 printPreOrderRec(currRoot.right);
127 }
128
129 /**
130 * Printing the contents of the tree in a Postorder way.
131 */
132 public void printPostorder() {
133 printPostOrderRec(root);
134 System.out.println( "" );
135 }
136
137 /**
138 * Helper method to recursively print the contents in a Postorder way
139 */
140 private void printPostOrderRec(Node currRoot) {
141 if (currRoot == null ) {
142 return ;
143 }
144 printPostOrderRec(currRoot.left);
145 printPostOrderRec(currRoot.right);
146 System.out.print(currRoot.value + ", " );
147
148 }
149 }
150
151 public class BinarySearchTreeDemo {
152
153 public static void main(String[] args) {
154 BinarySearchTree bst = new BinarySearchTree();
155 bst .insert( 40 )
156 .insert( 25 )
157 .insert( 78 )
158 .insert( 10 )
159 .insert( 3 )
160 .insert( 17 )
161 .insert( 32 )
162 .insert( 30 )
163 .insert( 38 )
164 .insert( 78 )
165 .insert( 50 )
166 .insert( 93 );
167 System.out.println( "Inorder traversal" );
168 bst.printInorder();
169
170 System.out.println( "Preorder Traversal" );
171 bst.printPreorder();
172
173 System.out.println( "Postorder Traversal" );
174 bst.printPostorder();
175
176 System.out.println( "The minimum value in the BST: " + bst.findMinimum());
177 System.out.println( "The maximum value in the BST: " + bst.findMaximum());
178
179 }
180 }
From Rosetta Code
Jump to: navigation, search
Binary Search Tree and Tree Traversal - Inorder, Preorder, Postorder implemented in Java
Tree traversal
You are encouraged to solve this task.

Implement a binary tree and implement the preoder, inorder, postorder and level-order traversal. Use the following tree tree:

  one
         / \
        / \
       / \
      2 3
     / \ /
    4 5 6
   / / \
  7 8 9

The correct output should look like this:

  preorder: 1 2 4 7 5 3 6 8 9
 inorder: 7 4 2 5 1 8 6 9 3
 postorder: 7 4 5 2 8 9 6 3 1
 level-order: 1 2 3 4 5 6 7 8 9

This article has more information on traversing trees.

Contents

[hide]
  • 1 ACL2
  • 2 Ada
  • 3 ALGOL 68
  • 4 ATS
  • 5 AutoHotkey
  • 6 bracmat
  • 7 C
  • 8 C #
  • 9 C ++
  • 10 Clojure
  • 11 CoffeeScript
  • 12 Common Lisp
  • 13 D
    • 13.1 Alternative Version
    • 13.2 Alternative Lazy Version
  • 14 E
  • 15 eiffel
  • 16 elisa
  • 17 Erlang
  • 18 euphoria
  • 19 F #
  • 20 factor
  • 21 Fantom
  • 22 Forth
  • 23 FunL
  • 24 go
    • 24.1 Individually allocated nodes
    • 24.2 Flat slice
  • 25 groovy
  • 26 haskell
  • 27 Icon and Unicon
  • 28 j
  • 29 java
  • 30 javascript
  • 31 jq
  • 32 Julia
  • 33 Logo
  • 34 logtalk
  • 35 Mathematica
  • 36 Nimrod
  • 37 objeck
  • 38 OCaml
  • 39 ooRexx
  • 40 oz
  • 41 perl
  • 42 perl 6
  • 43 PicoLisp
  • 44 Prolog
  • 45 PureBasic
  • 46 python
  • 47 Qi
  • 48 Racket
  • 49 rexx
  • 50 ruby
  • 51 Scala
  • 52 Tcl
  • 53 UNIX Shell
  • 54 Ursala
  • 55 zkl

[edit] ACL2

  ( defun flatten-preorder ( tree ) 
  ( if ( endp tree ) 
  nil 
  ( append ( list ( first tree ) ) 
  ( flatten-preorder ( second tree ) ) 
  ( flatten-preorder ( third tree ) ) ) ) ) 

  ( defun flatten-inorder ( tree ) 
  ( if ( endp tree ) 
  nil 
  ( append ( flatten-inorder ( second tree ) ) 
  ( list ( first tree ) ) 
  ( flatten-inorder ( third tree ) ) ) ) ) 

  ( defun flatten-postorder ( tree ) 
  ( if ( endp tree ) 
  nil 
  ( append ( flatten-postorder ( second tree ) ) 
  ( flatten-postorder ( third tree ) ) 
  ( list ( first tree ) ) ) ) ) 

  ( defun flatten-level-r1 ( tree level levels ) 
  ( if ( endp tree ) 
  levels 
  ( let ( ( curr ( cdr ( assoc level levels ) ) ) )) 
  ( flatten-level-r1 
  ( second tree ) 
  ( 1 + level ) 
  ( flatten-level-r1 
  ( third tree ) 
  ( 1 + level ) 
  ( put- assoc level 
  ( append curr ( list ( first tree ) ) ) 
  levels ) ) ) ) ) ) 

  ( defun flatten-level-r2 ( levels max-level ) 
  ( declare ( xargs : measure ( nfix ( 1 + max-level ) ) ) ) 
  ( if ( zp ( 1 + max-level ) ) 
  nil 
  ( append ( flatten-level-r2 levels 
  ( 1 - max-level ) ) 
  ( reverse ( cdr ( assoc max-level levels ) ) ) ) ) ) 


  ( defun flatten-level ( tree ) 
  ( let ( ( levels ( flatten-level-r1 tree 0 nil ) ) ) 
  ( flatten-level-r2 levels ( len levels ) ) ) )

[edit] Ada

  with Ada.  Text_Io ;  use Ada.  Text_Io ; 
  with Ada.  Unchecked_Deallocation ; 
  with Ada.  Containers .  Doubly_Linked_Lists ; 

  procedure Tree_Traversal is 
  type Node; 
  type Node_Access is access Node; 
  type Node is record 
  Left: Node_Access: = null ; 
  Right: Node_Access: = null ; 
  Data: Integer; 
  end record ; 
  procedure Destroy_Tree ( N: in out Node_Access ) is 
  procedure free is new Ada.  Unchecked_Deallocation ( Node, Node_Access ) ; 
  begin 
  if N. Left / = null then 
  Destroy_Tree ( N. Left ) ; 
  end if ; 
  if N. Right / = null then 
  Destroy_Tree ( N. Right ) ; 
  end if ; 
  Free ( N ) ; 
  end Destroy_Tree; 
  function Tree ( Value: Integer; Left: Node_Access; Right: Node_Access ) return Node_Access is 
  Temp: Node_Access: = new Node; 
  begin 
  Temp.  Data : = Value; 
  Temp.  Left : = Left; 
  Temp.  Right : = Right; 
  return Temp; 
  end tree; 
  procedure Preorder ( N: Node_Access ) is 
  begin 
  Put ( Integer'Image ( N. Data ) ) ; 
  if N. Left / = null then 
  Preorder ( N. Left ) ; 
  end if ; 
  if N. Right / = null then 
  Preorder ( N. Right ) ; 
  end if ; 
  end Preorder; 
  procedure Inorder ( N: Node_Access ) is 
  begin 
  if N. Left / = null then 
  Inorder ( N. Left ) ; 
  end if ; 
  Put ( Integer'Image ( N. Data ) ) ; 
  if N. Right / = null then 
  Inorder ( N. Right ) ; 
  end if ; 
  end inorder; 
  procedure Postorder ( N: Node_Access ) is 
  begin 
  if N. Left / = null then 
  Postorder ( N. Left ) ; 
  end if ; 
  if N. Right / = null then 
  Postorder ( N. Right ) ; 
  end if ; 
  Put ( Integer'Image ( N. Data ) ) ; 
  end postorder; 
  procedure Levelorder ( N: Node_Access ) is 
  package Queues is new Ada.  Containers .  Doubly_Linked_Lists ( Node_Access ) ; 
  use Queues; 
  Node_Queue: List; 
  Next: Node_Access; 
  begin 
  Node_Queue.  Append ( N ) ; 
  while not Is_Empty ( Node_Queue ) loop 
  Next: = First_Element ( Node_Queue ) ; 
  Delete_First ( Node_Queue ) ; 
  Put ( Integer'Image ( Next. Data ) ) ; 
  if next.  Left / = null then 
  Node_Queue.  Append ( Next. Left ) ; 
  end if ; 
  if next.  Right / = null then 
  Node_Queue.  Append ( Next. Right ) ; 
  end if ; 
  end loop ; 
  end levelorder; 
  N: Node_Access; 
  begin 
  N: = Tree ( 1 , 
  Tree ( 2 , 
  Tree ( 4 , 
  Tree ( 7 , null , null ) , 
  null ) , 
  Tree ( 5 , null , null ) ) , 
  Tree ( 3 , 
  Tree ( 6 , 
  Tree ( 8 , null , null ) , 
  Tree ( 9 , null , null ) ) , 
  null ) ) ; 

  Put ( "preorder:" ) ; 
  Preorder ( N ) ; 
  New_Line; 
  Put ( "inorder:" ) ; 
  Inorder ( N ) ; 
  New_Line; 
  Put ( "postorder:" ) ; 
  Postorder ( N ) ; 
  New_Line; 
  Put ( "level order:" ) ; 
  Levelorder ( N ) ; 
  New_Line; 
  Destroy_Tree ( N ) ; 
  end Tree_traversal;

[edit] ALGOL 68

Translation of : C
- note the strong code structural similarities with C.

C this diff. It contains examples of syntactic sugar available in ALGOL 68.

Works with : ALGOL 68 version Standard - no extensions to language used
Works with : ALGOL 68G version Any - tested with release 1.18.0-9h.tiny
Works with : ELLA ALGOL 68 version Any (with appropriate job cards)
  MODE VALUE = INT ; 
  PROC value repr = ( VALUE value ) STRING : whole ( value , 0 ) ; 

  MODE NODES = STRUCT ( VALUE value , REF NODES left , right ) ; 
  MODE NODE = REF NODES ; 

  PROC tree = ( VALUE value , NODE left , right ) NODE : 
  HEAP NODES : = ( value , left , right ) ; 

  PROC preorder = ( NODE node , PROC ( VALUE ) VOID action ) VOID : 
  IF node ISNT NODE ( NIL ) THEN 
  action ( value OF node ) ; 
  preorder ( left OF node , action ) ; 
  preorder ( right OF node , action ) 
  FI ; 

  PROC inorder = ( NODE node , PROC ( VALUE ) VOID action ) VOID : 
  IF node ISNT NODE ( NIL ) THEN 
  inorder ( left OF node , action ) ; 
  action ( value OF node ) ; 
  inorder ( right OF node , action ) 
  FI ; 

  PROC postorder = ( NODE node , PROC ( VALUE ) VOID action ) VOID : 
  IF node ISNT NODE ( NIL ) THEN 
  postorder ( left OF node , action ) ; 
  postorder ( right OF node , action ) ; 
  action ( value OF node ) 
  FI ; 

  PROC destroy tree = ( NODE node ) VOID : 
  postorder ( node , ( VALUE skip ) VOID : 
  # free (node) - PR garbage collect hint PR # 
  node : = ( SKIP , NIL , NIL ) 
  ) ; 

  # helper queue for level order # 
  MODE QNODES = STRUCT ( REF QNODES next , NODE value ) ; 
  MODE QNODE = REF QNODES ; 


  MODE QUEUES = STRUCT ( QNODE begin , end ) ; 
  MODE QUEUE = REF QUEUES ; 

  PROC enqueue = ( QUEUE queue , NODE node ) VOID : 
  ( 
  HEAP QNODES qnode : = ( NIL , node ) ; 
  IF end OF queue ISNT QNODE ( NIL ) THEN 
  next OF end OF queue 
  ELSE 
  begin OF queue 
  FI : = end OF queue : = qnode 
  ) ; 

  PROC queue empty = ( QUEUE queue ) BOOL : 
  begin OF queue IS QNODE ( NIL ) ; 

  PROC dequeue = ( QUEUE queue ) NODE : 
  ( 
  NODE out : = value OF begin OF queue ; 
  QNODE second : = next OF begin OF queue ; 
  # free (begin OF queue);  PR garbage collect hint PR # 
  QNODE ( begin OF queue ) : = ( NIL , NIL ) ; 
  begin OF queue : = second ; 
  IF queue empty ( queue ) THEN 
  end OF queue : = begin OF queue 
  FI ; 
  out 
  ) ; 

  PROC level order = ( NODE node , PROC ( VALUE ) VOID action ) VOID : 
  ( 
  HEAP QUEUES queue : = ( QNODE ( NIL ) , QNODE ( NIL ) ) ; 
  enqueue ( queue , node ) ; 
  WHILE NOT queue empty ( queue ) 
  Do 
  NODE next : = dequeue ( queue ) ; 
  IF next ISNT NODE ( NIL ) THEN 
  action ( value OF next ) ; 
  enqueue ( queue , left OF next ) ; 
  enqueue ( queue , right OF next ) 
  FI 
  Od 
  ) ; 

  PROC print node = ( VALUE value ) VOID : 
  print ( ( "" , value repr ( value ) ) ) ; 

  main : ( 
  NODE node : = tree ( 1 , 
  tree ( 2 , 
  tree ( 4 , 
  tree ( 7 , NIL , NIL ) , 
  NIL ) 
  tree ( 5 , NIL , NIL ) ) , 
  tree ( 3 , 
  tree ( 6 , 
  tree ( 8 , NIL , NIL ) , 
  tree ( 9 , NIL , NIL ) ) , 
  NIL ) ) ; 

  MODE TEST = STRUCT ( 
  STRING name , 
  PROC ( NODE , PROC ( VALUE ) VOID ) VOID order 
  ) ; 

  PROC test = ( TEST test ) VOID : ( 
  STRING pad = "" * ( 12 - UPB name OF test ) ; 
  print ( ( name OF test , pad , ":" ) ) ; 
  ( order OF test ) ( node , print node ) ; 
  print ( new line ) 
  ) ; 

  [ ] TEST test list = ( 
  ( "preorder" , preorder ) , 
  ( "inorder" , inorder ) , 
  ( "postorder" , postorder ) , 
  ( "level order" , level order ) 
  ) ; 

  FOR i TO UPB test list DO test ( test list [ i ] ) OD ; 

  destroy tree ( node ) 
  )

Output:

  preorder: 1 2 4 7 5 3 6 8 9 
 inorder: 7 4 2 5 1 8 6 9 3 
 postorder: 7 4 5 2 8 9 6 3 1 
 level-order: 1 2 3 4 5 6 7 8 9

[edit] ATS

  #include 
  "share / atspre_staload.hats" 
  // 
  (* ****** ****** *) 
  // 
  datatype 
  tree (a: t @ ype) = 
  |  tnil of () 
  |  tcons of (tree a, a, tree a) 
  // 
  (* ****** ****** *) 

  symintr ++ 
  infixr (+) ++ 
  overload ++ with list_append 

  (* ****** ****** *) 

  #define sing list_sing 

  (* ****** ****** *) 

  fun { 
  a: t @ ype 
  } preorder 
  (t0: tree a): List0 a = 
  case t0 of 
  |  tnil () => nil () 
  |  tcons (tl, x, tr) => sing (x) ++ preorder (tl) ++ preorder (tr) 

  (* ****** ****** *) 

  fun { 
  a: t @ ype 
  } inorder 
  (t0: tree a): List0 a = 
  case t0 of 
  |  tnil () => nil () 
  |  tcons (tl, x, tr) => inorder (tl) ++ sing (x) ++ inorder (tr) 

  (* ****** ****** *) 

  fun { 
  a: t @ ype 
  } postorder 
  (t0: tree a): List0 a = 
  case t0 of 
  |  tnil () => nil () 
  |  tcons (tl, x, tr) => postorder (tl) ++ postorder (tr) ++ sing (x) 

  (* ****** ****** *) 

  fun { 
  a: t @ ype 
  } levelorder 
  (t0: tree a): List0 a = let 
  // 
  fun auxlst 
  (ts: List (tree (a))): List0 a = 
  case ts of 
  |  list_nil () => list_nil () 
  |  list_cons (t, ts) => 
  ( 
  case + t of 
  |  tnil () => auxlst (ts) 
  |  tcons (tl, x, tr) => cons (x, auxlst (ts ++ $ list {tree (a)} (tl, tr))) 
  ) 
  // 
  in 
  auxlst (sing (t0)) 
  end // end of [levelorder] 

  (* ****** ****** *) 

  macdef 
  tsing (x) = tcons (tnil,, (x), tnil) 

  (* ****** ****** *) 

  implement 
  main0 () = let 
  // 
  val t0 = 
  tcons {int} 
  ( 
  tcons (tcons (tsing (7), 4, tnil ()), 2, tsing (5)) 
  , 
  one 
  , 
  tcons (tcons (tsing (8), 6, tsing (9)), 3, tnil () 
  ) 
  // 
  in 
  println!  ("preorder: \ t", preorder (t0)); 
  println!  ("inorder: \ t", inorder (t0)); 
  println!  ("postorder: \ t", postorder (t0)); 
  println!  ("level-order: \ t", levelorder (t0)); 
  end (* end of [main0] *)

Output:

  preorder: 1 2 4 7 5 3 6 8 9 
 inorder: 7 4 2 5 1 8 6 9 3 
 postorder: 7 4 5 2 8 9 6 3 1 
 level-order: 1 2 3 4 5 6 7 8 9

[edit] AutoHotkey

Works with : AutoHotkey_L version 45
  AddNode ( Tree , 1 , 2 , 3 , 1 ) ;  Build global tree 
  AddNode ( Tree , 2 , 4 , 5 , 2 ) 
  AddNode ( Tree , 3 , 6 , 0 , 3 ) 
  AddNode ( Tree , 4 , 7 , 0 , 4 ) 
  AddNode ( Tree , 5 , 0 , 0 , 5 ) 
  AddNode ( Tree , 6 , 8 , 9 , 6 ) 
  AddNode ( Tree , 7 , 0 , 0 , 7 ) 
  AddNode ( Tree , 8 , 0 , 0 , 8 ) 
  AddNode ( Tree , 9 , 0 , 0 , 9 ) 

  MsgBox % "Preorder:" PreOrder ( Tree , 1 ) ;  1 2 4 7 5 3 6 8 9 
  MsgBox % "Inorder:" InOrder ( Tree , 1 ) ;  7 4 2 5 1 8 6 9 3 
  MsgBox % "postorder:" PostOrder ( Tree , 1 ) ;  7 4 5 2 8 9 6 3 1 
  MsgBox % "levelorder:" LevOrder ( Tree , 1 ) ;  1 2 3 4 5 6 7 8 9 

  AddNode ( ByRef Tree , Node , Left , Right , Value ) { 
  if ! isobject ( Tree ) 
  Tree : = object ( ) 

  Tree [ Node , "L" ] : = Left 
  Tree [ Node , "R" ] : = Right 
  Tree [ Node , "V" ] : = Value 
  } 

  PreOrder ( Tree , Node ) { 
  ptree : = Tree [ Node , "V" ] "" 
  .  ( ( L : = Tree [ Node , "L" ] ) ? PreOrder ( Tree , L ) : "" ) 
  .  ( ( R : = Tree [ Node , "R" ] ) ? PreOrder ( Tree , R ) : "" ) 
  return ptree 
  } 
  InOrder ( Tree , Node ) { 
  Return itree : = ( ( L : = Tree [ Node , "L" ] ) ? InOrder ( Tree , L ) : "" ) 
  .  Tree [ Node , "V" ] "" 
  .  ( ( R : = Tree [ Node , "R" ] ) ? InOrder ( Tree , R ) : "" ) 
  } 
  PostOrder ( Tree , Node ) { 
  Return ptree : = ( ( L : = Tree [ Node , "L" ] ) ? PostOrder ( Tree , L ) : "" ) 
  .  ( ( R : = Tree [ Node , "R" ] ) ? PostOrder ( Tree , R ) : "" ) 
  .  Tree [ Node , "V" ] "" 
  } 
  LevOrder ( Tree , Node , Lev = 1 ) { 
  Static ;  make node lists static 
  i % Lev% . = Tree [ Node , "V" ] "" ;  build node lists in every level 
  If ( L : = Tree [ Node , "L" ] ) 
  LevOrder ( Tree , L , Lev + 1 ) 
  If ( R : = Tree [ Node , "R" ] ) 
  LevOrder ( Tree , R , Lev + 1 ) 
  If ( Lev > 1 ) 
  Return 
  While i % Lev% ;  concatenate node lists from all levels 
  t . = i % Lev% , Lev ++ 
  Return t 
  }

[edit] Bracmat

  ( 
  (tree 
  = 1 
  .  (2. (4.7.) (5.)) 
  (3.6. (8.) (9.)) 
  ) 
  & (preorder 
  = K sub 
  .  ! arg :(? K.?sub)? arg 
  &! K preorder $! Sub preorder $! Arg 
  | 
  ) 
  & out $ ("preorder:" preorder $! tree) 
  & (inorder 
  = K lhs rhs 
  .  ! arg :(? K.?sub)? arg 
  & (! sub:%? lhs? rhs 
  & inorder $! lhs! K inorder $! rhs inorder $! arg 
  |  ! K 
  ) 
  ) 
  & out $ ("inorder:" inorder $! tree) 
  & (postorder 
  = K sub 
  .  ! arg :(? K.?sub)? arg 
  & postorder $! sub! K postorder $! arg 
  | 
  ) 
  & out $ ("postorder:" postorder $! tree) 
  & (levelorder 
  = todo tree sub 
  .  ! arg: (.) ​​& 
  |  ! arg :(? tree.?todo) 
  & (! tree :(? K.?sub)? tree 
  &! K levelorder $ (! Tree.! Todo! Sub) 
  |  levelorder $ (! todo.) 
  ) 
  ) 
  & out $ ("level-order:" levelorder $ (! tree.)) 
  & 
  )

[edit] C

  #include  
  #include  

  typedef struct node_s 
  { 
  int value ; 
  struct node_s * left ; 
  struct node_s * right ; 
  } * node ; 

  node tree ( int v , node l , node r ) 
  { 
  node n = malloc ( sizeof ( struct node_s ) ) ; 
  n -> value = v ; 
  n -> left = l ; 
  n -> right = r ; 
  return n ; 
  } 

  void destroy_tree ( node n ) 
  { 
  if ( n -> left ) 
  destroy_tree ( n -> left ) ; 
  if ( n -> right ) 
  destroy_tree ( n -> right ) ; 
  free ( n ) ; 
  } 

  void preorder ( node n , void ( * f ) ( int ) ) 
  { 
  f ( n -> value ) ; 
  if ( n -> left ) 
  preorder ( n -> left , f ) ; 
  if ( n -> right ) 
  preorder ( n -> right , f ) ; 
  } 

  void inorder ( node n , void ( * f ) ( int ) ) 
  { 
  if ( n -> left ) 
  inorder ( n -> left , f ) ; 
  f ( n -> value ) ; 
  if ( n -> right ) 
  inorder ( n -> right , f ) ; 
  } 

  void postorder ( node n , void ( * f ) ( int ) ) 
  { 
  if ( n -> left ) 
  postorder ( n -> left , f ) ; 
  if ( n -> right ) 
  postorder ( n -> right , f ) ; 
  f ( n -> value ) ; 
  } 

  / * helper queue for levelorder * / 
  typedef struct qnode_s 
  { 
  struct qnode_s * next ; 
  node value ; 
  } * qnode ; 

  typedef struct { qnode begin , end ;  } queue ; 

  void enqueue ( queue * q , node n ) 
  { 
  qnode node = malloc ( sizeof ( struct qnode_s ) ) ; 
  node -> value = n ; 
  node -> next = 0 ; 
  if ( q -> end ) 
  q -> end -> next = node ; 
  else 
  q -> begin = node ; 
  q -> end = node ; 
  } 

  node dequeue ( queue * q ) 
  { 
  node tmp = q -> begin -> value ; 
  qnode second = q -> begin -> next ; 
  free ( q -> begin ) ; 
  q -> begin = second ; 
  if ( ! q -> begin ) 
  q -> end = 0 ; 
  return tmp ; 
  } 

  int queue_empty ( queue * q ) 
  { 
  return !  q -> begin ; 
  } 

  void levelorder ( node n , void ( * f ) ( int ) ) 
  { 
  queue nodequeue = { } ; 
  enqueue ( & nodequeue , n ) ; 
  while ( ! queue_empty ( & nodequeue ) ) 
  { 
  node next = dequeue ( & nodequeue ) ; 
  f ( next -> value ) ; 
  if ( next -> left ) 
  enqueue ( & nodequeue , next -> left ) ; 
  if ( next -> right ) 
  enqueue ( & nodequeue , next -> right ) ; 
  } 
  } 

  void print ( int n ) 
  { 
  printf ( "% d" , n ) ; 
  } 

  int main ( ) 
  { 
  node n = tree ( 1 , 
  tree ( 2 , 
  tree ( 4 , 
  tree ( 7 , 0 , 0 ) 
  0 ) 
  tree ( 5 , 0 , 0 ) ) , 
  tree ( 3 , 
  tree ( 6 , 
  tree ( 8 , 0 , 0 ) 
  tree ( 9 , 0 , 0 ) ) , 
  0 ) ) ; 

  printf ( "preorder:" ) ; 
  preorder ( n , print ) ; 
  printf ( " \ n " ) ; 

  printf ( "inorder:" ) ; 
  inorder ( n , print ) ; 
  printf ( " \ n " ) ; 

  printf ( "postorder:" ) ; 
  postorder ( n , print ) ; 
  printf ( " \ n " ) ; 

  printf ( "level-order:" ) ; 
  levelorder ( n , print ) ; 
  printf ( " \ n " ) ; 

  destroy_tree ( n ) ; 

  return 0 ; 
  }

[edit] C #

  using System ; 
  using System.Collections.Generic ; 
  using System.Linq ; 

  class Node 
  { 
  int value ; 
  Node Left ; 
  Node Right ; 

  Node ( int value = default ( int ) , Node left = default ( Node ) , Node right = default ( Node ) ) 
  { 
  Value = value ; 
  Left = left ; 
  Right = right ; 
  } 

  IEnumerable < int > Preorder ( ) 
  { 
  yield return Value ; 
  if ( Left ! = null ) 
  foreach ( var value in Left . Preorder ( ) ) 
  yield return value ; 
  if ( Right ! = null ) 
  foreach ( var value in Right . Preorder ( ) ) 
  yield return value ; 
  } 

  IEnumerable < int > Inorder ( ) 
  { 
  if ( Left ! = null ) 
  foreach ( var value in Left . Inorder ( ) ) 
  yield return value ; 
  yield return Value ; 
  if ( Right ! = null ) 
  foreach ( var value in Right . Inorder ( ) ) 
  yield return value ; 
  } 

  IEnumerable < int > Postorder ( ) 
  { 
  if ( Left ! = null ) 
  foreach ( var value in Left . Postorder ( ) ) 
  yield return value ; 
  if ( Right ! = null ) 
  foreach ( var value in Right . Postorder ( ) ) 
  yield return value ; 
  yield return Value ; 
  } 

  IEnumerable < int > LevelOrder ( ) 
  { 
  var queue = new Queue < Node > ( ) ; 
  queue .  Enqueue ( this ) ; 
  while ( queue . Any ( ) ) 
  { 
  var node = queue .  Dequeue ( ) ; 
  yield return node .  Value ; 
  if ( node . Left ! = null ) 
  queue .  Enqueue ( node . Left ) ; 
  if ( node . Right ! = null ) 
  queue .  Enqueue ( node . Right ) ; 
  } 
  } 

  static void Main ( ) 
  { 
  var tree = new Node ( 1 , new Node ( 2 , new Node ( 4 , new Node ( 7 ) ) , new Node ( 5 ) ) , new Node ( 3 , new Node ( 6 , new Node ( 8 ) , new Node ( 9 ) ) ) ) ; 
  foreach ( var traversal func < IEnumerable < int >> [ ] { tree . Preorder , tree . Inorder , tree . Postorder , tree . LevelOrder } ) 
  Console .  WriteLine ( "{0}: \ t {1}" , traversal . Method . Name , string . Join ( "" , traversal ( ) ) ) ; 
  } 
  }

[edit] C ++

Compiler: g ++ (version 4.3.2 20081105 (Red Hat 4.3.2-7))

Library: Boost version 1.39.0
  #include  
  #include  
  #include  

  template < typename T > 
  class TreeNode { 
  public : 
  TreeNode ( const T & n, TreeNode * left = NULL , TreeNode * right = NULL ) 
  : mValue ( n ) , 
  mLeft ( left ) , 
  mRight ( right ) { } 

  T getValue ( ) const { 
  return mValue ; 
  } 

  TreeNode * left ( ) const { 
  return mLeft.  get ( ) ; 
  } 

  TreeNode * right ( ) const { 
  return mRight.  get ( ) ; 
  } 

  void preorderTraverse ( ) const { 
  std :: cout << "" << getValue ( ) ; 
  if ( mLeft ) { mLeft - > preorderTraverse ( ) ;  } 
  if ( mRight ) { mRight - > preorderTraverse ( ) ;  } 
  } 

  void inorderTraverse ( ) const { 
  if ( mLeft ) { mLeft - > inorderTraverse ( ) ;  } 
  std :: cout << "" << getValue ( ) ; 
  if ( mRight ) { mRight - > inorderTraverse ( ) ;  } 
  } 

  void postorderTraverse ( ) const { 
  if ( mLeft ) { mLeft - > postorderTraverse ( ) ;  } 
  if ( mRight ) { mRight - > postorderTraverse ( ) ;  } 
  std :: cout << "" << getValue ( ) ; 
  } 

  void levelorderTraverse ( ) const { 
  std :: queue < const TreeNode * > q ; 
  q.  push ( this ) ; 

  while ( ! q. empty ( ) ) { 
  const TreeNode * n = q.  front ( ) ; 
  q.  pop ( ) ; 
  std :: cout << "" << n - > getValue ( ) ; 

  if ( n - > left ( ) ) { q.  push ( n - > left ( ) ) ;  } 
  if ( n - > right ( ) ) { q.  push ( n - > right ( ) ) ;  } 
  } 
  } 

  protected : 
  T mValue ; 
  boost :: scoped_ptr < TreeNode > mLeft ; 
  boost :: scoped_ptr < TreeNode > mRight ; 

  private : 
  TreeNode ( ) ; 
  } ; 

  int main ( ) { 
  TreeNode < int > root ( 1 , 
  new TreeNode < int > ( 2 , 
  new TreeNode < int > ( 4 , 
  new TreeNode < int > ( 7 ) ) , 
  new TreeNode < int > ( 5 ) ) , 
  new TreeNode < int > ( 3 , 
  new TreeNode < int > ( 6 , 
  new TreeNode < int > ( 8 ) , 
  new TreeNode < int > ( 9 ) ) ) ) ; 

  std :: cout << "preorder:" ; 
  root  preorderTraverse ( ) ; 
  std :: cout << std :: endl ; 

  std :: cout << "inorder:" ; 
  root  inorderTraverse ( ) ; 
  std :: cout << std :: endl ; 

  std :: cout << "postorder:" ; 
  root  postorderTraverse ( ) ; 
  std :: cout << std :: endl ; 

  std :: cout << "level-order:" ; 
  root  levelorderTraverse ( ) ; 
  std :: cout << std :: endl ; 

  return 0 ; 
  }

[edit] Clojure

  ( defn walk [ node f order ] 
  ( when node 
  ( doseq [ o order ] 
  ( if ( = o: visit ) 
  ( f ( : val node ) ) 
  ( walk ( node o ) f order ) ) ) ) ) 

  ( defn preorder [ node f ] 
  ( walk node f [ : visit : left : right ] ) ) 

  ( defn inorder [ node f ] 
  ( walk node f [ : left : visit : right ] ) ) 

  ( defn postorder [ node f ] 
  ( walk node f [ : left : right : visit ] ) ) 

  ( defn queue [ & xs ] 
  ( when ( seq xs ) 
  ( apply conj clojure . lang . PersistentQueue / EMPTY xs ) ) ) 

  ( defn level - order [ root f ] 
  ( loop [ q ( queue root ) ] 
  ( when-not ( empty? q ) 
  ( if-let [ node ( first q ) ] 
  ( do 
  ( f ( : val node ) ) 
  ( recur ( conj ( pop q ) ( : left node ) ( : right node ) ) ) )) 
  ( recur ( pop q ) ) ) ) ) ) 

  ( defn vec - to - tree [ t ] 
  ( if ( vector? t ) 
  ( let [ [ val left right ] t ] 
  { : val 
  : left ( vec - to - tree left ) 
  : right ( vec - to - tree right ) } ) 
  t ) ) 

  ( let [ tree ( vec - to - tree [ 1 [ 2 [ 4 [ 7 ] ] [ 5 ] ] [ 3 [ 6 [ 8 ] [ 9 ] ] ] ] ) 
  fs' [ preorder inorder postorder level - order ] 
  pr - node # ( print ( format "% 2d" % ) ) ] 
  ( doseq [ f fs ] 
  ( print ( format "% -12s" ( str f ":" ) ) ) 
  ( ( resolve f ) tree pr - node ) 
  ( println ) ) )

[edit] CoffeeScript

  # In this example, we don’t encapsulate binary trees as objects;  instead, we have a 
  # convention on how to store them 
  # operate on those data structures. 
  binary_tree = 
  preorder : ( tree , visit ) -> 
  return unless tree ? 
  [ node , left , right ] = tree 
  visit node 
  binary_tree.  preorder left , visit 
  binary_tree.  preorder right visit 

  inorder : ( tree , visit ) -> 
  return unless tree ? 
  [ node , left , right ] = tree 
  binary_tree.  inorder left , visit 
  visit node 
  binary_tree.  inorder right , visit 

  postorder : ( tree , visit ) -> 
  return unless tree ? 
  [ node , left , right ] = tree 
  binary_tree.  postorder left , visit 
  binary_tree.  postorder right visit 
  visit node 

  Levelorder : ( tree , visit ) -> 
  q = [ ] 
  q.  push tree 
  while q.  length > 0 
  t = q.  shift ( ) 
  continue unless t ? 
  [ node , left , right ] = t 
  visit node 
  q.  push left 
  q.  push right 

  do -> 
  tree = [ 1 , [ 2 , [ 4 , [ 7 ] ] , [ 5 ] ] , [ 3 , [ 6 , [ 8 ] , [ 9 ] ] ] 
  test_walk = ( walk_function_name ) -> 
  output = [ ] 
  binary_tree [ walk_function_name ] tree , output.  push .  bind ( output ) 
  console.  log walk_function_name , output.  join '' 
  test_walk "preorder" 
  test_walk "inorder" 
  test_walk "postorder" 
  test_walk "levelorder"

output

  > coffee tree_traversal.coffee 
  preorder 1 2 4 7 5 3 6 8 9 
  inorder 7 4 2 5 1 8 6 9 3 
  postorder 7 4 5 2 8 9 6 3 1 
  levelorder 1 2 3 4 5 6 7 8 9

[edit] Common Lisp

  ( defun preorder ( node f ) 
  ( when node 
  ( funcall f ( first node ) ) 
  ( preorder ( second node ) f ) 
  ( preorder ( third node ) f ) ) ) 

  ( defun inorder ( node f ) 
  ( when node 
  ( inorder ( second node ) f ) 
  ( funcall f ( first node ) ) 
  ( inorder ( third node ) f ) ) ) 

  ( defun postorder ( node f ) 
  ( when node 
  ( postorder ( second node ) f ) 
  ( postorder ( third node ) f ) 
  ( funcall f ( first node ) ) ) ) 

  ( defun level-order ( node f ) 
  ( loop with level = ( list node ) 
  while level 
  do 
  ( setf level ( loop for node in level 
  when node 
  do ( funcall f ( first node ) ) 
  and collect ( second node ) 
  and collect ( third node ) ) ) ) ) 

  ( defparameter * tree * ' ( 1 ( 2 ( 4 ( 7 ) ) 
  ( 5 ) ) 
  ( 3 ( 6 ( 8 ) 
  ( 9 ) ) ) ) ) 

  ( defun show ( traversal- function ) 
  ( format t "~ & ~ (~ A ~): ~ 12.0T" traversal- function ) 
  ( funcall traversal- function * tree * ( lambda ( value ) ( format t "~ A" value ) ) ) ) 

  ( map nil # 'show' ( preorder inorder postorder level-order ) )

Output:

  preorder: 1 2 4 7 5 3 6 8 9
 inorder: 7 4 2 5 1 8 6 9 3
 postorder: 7 4 2 5 1 8 6 9 3
 level-order: 1 2 3 4 5 6 7 8 9

[edit] D

This code is long because it's very generic.

  import std.  stdio , std.  traits ; 

  const final class Node ( T ) { 
  T data ; 
  Node left , right ; 

  this ( in T data , in Node left = null , in Node right = null ) 
  const pure nothrow { 
  this .  data = data ; 
  this .  left = left ; 
  this .  right = right ; 
  } 
  } 

  // 'static' templated opCall can't be used in Node 
  auto node ( T ) ( in T data , in Node ! T left = null , in Node ! T right = null ) 
  pure nothrow { 
  return new const ( Node ! T ) ( data , left , right ) ; 
  } 

  void show ( T ) ( in T x ) { 
  write ( x , "" ) ; 
  } 

  enum Visit { pre , inv , post } 

  // 'visitor' it is a default visitor. 
  // TNode can be any kind of Node, with data, left and right fields, 
  // so this is more generic than a member function of Node. 
  void backtrackingOrder ( Visit v , TNode , TyF = void * ) 
  ( in TNode node , TyF visitor = null ) { 
  alias trueVisitor = Select !  ( is ( TyF == void * ) , show , visitor ) ; 
  if ( node ! is null ) { 
  static if ( v == Visit. pre ) 
  trueVisitor ( node. data ) ; 
  backtrackingOrder !  v ( node. left , visitor ) ; 
  static if ( v == Visit. inv ) 
  trueVisitor ( node. data ) ; 
  backtrackingOrder !  v ( node. right , visitor ) ; 
  static if ( v == Visit. post ) 
  trueVisitor ( node. data ) ; 
  } 
  } 

  void levelOrder ( TNode , TyF = void * ) 
  ( TNode node , TyF visitor = null , 
  const ( TNode ) [ ] more = [ ] ) { 
  alias trueVisitor = Select !  ( is ( TyF == void * ) , show , visitor ) ; 
  if ( node ! is null ) { 
  more ~ = [ node.  left , node.  right ] ; 
  trueVisitor ( node. data ) ; 
  } 
  if ( more. length ) 
  levelOrder ( more [ 0 ] , visitor , more [ 1 .. $ ] ) ; 
  } 

  void main ( ) { 
  alias N = node ; 
  const tree = N ( 1 , 
  N ( 2 , 
  N ( 4 , 
  N ( 7 ) ) 
  N ( 5 ) ) , 
  N ( 3 , 
  N ( 6 , 
  N ( 8 ) , 
  N ( 9 ) ) ) ) ; 

  write ( "preOrder:" ) ; 
  tree.  backtrackingOrder !  ( Visit. Pre ) ; 
  write ( " \ n inorder:" ) ; 
  tree.  backtrackingOrder !  ( Visit. Inv ) ; 
  write ( " \ n postOrder:" ) ; 
  tree.  backtrackingOrder !  ( Visit. Post ) ; 
  write ( " \ n levelorder:" ) ; 
  tree.  levelOrder ; 
  writeln ; 
  }

Output:

  preOrder: 1 2 4 7 5 3 6 8 9 
    inorder: 7 4 2 5 1 8 6 9 3 
  postOrder: 7 4 5 2 8 9 6 3 1 
 levelorder: 1 2 3 4 5 6 7 8 9

[edit] Alternative Version

Translation of : Haskell

Generic as the first version, but not the lazy as the Haskell version.

  const struct node ( t ) { 
  T v ; 
  Node * l , r ; 
  } 

  T [ ] preOrder ( T ) ( in Node ! T * t ) pure nothrow { 
  return t ?  t.  v ~ preOrder ( t. l ) ~ preOrder ( t. r ) : [ ] ; 
  } 

  T [ ] inOrder ( T ) ( in Node ! T * t ) pure nothrow { 
  return t ?  inOrder ( t. l ) ~ t.  v ~ inOrder ( t. r ) : [ ] ; 
  } 

  T [ ] postOrder ( T ) ( in Node ! T * t ) pure nothrow { 
  return t ?  postOrder ( t. l ) ~ postOrder ( t. r ) ~ t.  v : [ ] ; 
  } 

  T [ ] levelOrder ( T ) ( in Node ! T * t ) pure nothrow { 
  static T [ ] loop ( in Node ! T * [ ] a ) pure nothrow { 
  if ( ! a. length ) return [ ] ; 
  if ( ! a [ 0 ] ) return loop ( a [ 1 .. $ ] ) ; 
  return a [ 0 ] .  v ~ loop ( a [ 1 .. $ ] ~ [ a [ 0 ] . l , a [ 0 ] . r ] ) ; 
  } 
  return loop ( [ t ] ) ; 
  } 

  void main ( ) { 
  alias N = Node !  int ; 
  auto tree = new N ( 1 , 
  new N ( 2 , 
  new N ( 4 , 
  new N ( 7 ) ) , 
  new N ( 5 ) ) , 
  new N ( 3 , 
  new N ( 6 , 
  new N ( 8 ) , 
  new N ( 9 ) ) ) ) ; 

  import std.  stdio ; 
  writeln ( preOrder ( tree ) ) ; 
  writeln ( inOrder ( tree ) ) ; 
  writeln ( postOrder ( tree ) ) ; 
  writeln ( levelOrder ( tree ) ) ; 
  }

Output:

  [1, 2, 4, 7, 5, 3, 6, 8, 9]
 [7, 4, 2, 5, 1, 8, 6, 9, 3]
 [7, 4, 5, 2, 8, 9, 6, 3, 1]
 [1, 2, 3, 4, 5, 6, 7, 8, 9]

[edit] Alternative Lazy Version

This is not a complete order visit.

  import std.  stdio , std.  algorithm , std.  range , std.  string ; 

  const struct Tree ( T ) { 
  T value ; 
  Tree * left , right ; 
  } 

  alias VisitRange ( T ) = InputRange !  ( const Tree ! T ) ; 

  VisitRange !  T preOrder ( T ) ( in Tree ! T * t ) / * pure nothrow * / { 
  enum self = mixin ( "&" ~ __FUNCTION__. split ( "." ) . back ) ; 
  if ( t == null ) 
  return typeof ( return ) .  init .  takeNone .  inputRangeObject ; 
  return [ * t ] 
  .  chain ( [ t. left , t. right ] 
  .  filter !  ( t => t ! = null ) 
  .  map !  ( a => self ( a ) ) 
  .  joiner ) 
  .  inputRangeObject ; 
  } 

  VisitRange !  T inOrder ( T ) ( in Tree ! T * t ) / * pure nothrow * / { 
  enum self = mixin ( "&" ~ __FUNCTION__. split ( "." ) . back ) ; 
  if ( t == null ) 
  return typeof ( return ) .  init .  takeNone .  inputRangeObject ; 
  return [ t.  left ] 
  .  filter !  ( t => t ! = null ) 
  .  map !  ( a => self ( a ) ) 
  .  joiner 
  .  chain ( [ * t ] ) 
  .  chain ( [ t. right ] 
  . filter ! ( t => t != null ) 
  . map ! ( a => self ( a ) ) 
  . joiner ) 
  . inputRangeObject ; 
  } 

 VisitRange ! T postOrder ( T ) ( in Tree ! T * t ) /*pure nothrow*/ { 
 enum self = mixin ( "&" ~ __FUNCTION__. split ( "." ) . back ) ; 
 if ( t == null ) 
 return typeof ( return ) . init . takeNone . inputRangeObject ; 
 return [ t. left , t. right ] 
  . filter ! ( t => t != null ) 
  . map ! ( a => self ( a ) ) 
  . joiner 
  . chain ( [ * t ] ) 
  . inputRangeObject ; 
  } 

 void main ( ) { 
 alias N = Tree ! int ; 
 const tree = new N ( 1 , 
 new N ( 2 , 
 new N ( 4 , 
 new N ( 7 ) ) , 
 new N ( 5 ) ) , 
 new N ( 3 , 
 new N ( 6 , 
 new N ( 8 ) , 
 new N ( 9 ) ) ) ) ; 

 tree. preOrder . map ! ( t => t. value ) . writeln ; 
 tree. inOrder . map ! ( t => t. value ) . writeln ; 
 tree. postOrder . map ! ( t => t. value ) . writeln ; 
  }

Output:

 [1, 2, 4, 7, 5, 3, 6, 8, 9]
[7, 4, 2, 5, 1, 8, 6, 9, 3]
[7, 4, 5, 2, 8, 9, 6, 3, 1]

[edit] E

 def btree := [ 1 , [ 2 , [ 4 , [ 7 , null , null ] , 
 null ] , 
 [ 5 , null , null ] ] , 
 [ 3 , [ 6 , [ 8 , null , null ] , 
 [ 9 , null , null ] ] , 
 null ] ] 

 def backtrackingOrder ( node , pre , mid , post ) { 
 switch ( node ) { 
 match == null { } 
 match [ value , left , right ] { 
 pre ( value ) 
 backtrackingOrder ( left , pre , mid , post ) 
 mid ( value ) 
 backtrackingOrder ( right , pre , mid , post ) 
 post ( value ) 
  } 
  } 
  } 

 def levelOrder ( root , func ) { 
 var level := [ root ] . diverge ( ) 
 while ( level. size ( ) > 0 ) { 
 for node in level. removeRun ( 0 ) { 
 switch ( node ) { 
 match == null { } 
 match [ value , left , right ] { 
 func ( value ) 
 level. push ( left ) 
 level. push ( right ) 
 } } } } } 

 print ( "preorder: " ) 
 backtrackingOrder ( btree , fn v { print ( " " , v ) } , fn _ { } , fn _ { } ) 
 println ( ) 

 print ( "inorder: " ) 
 backtrackingOrder ( btree , fn _ { } , fn v { print ( " " , v ) } , fn _ { } ) 
 println ( ) 

 print ( "postorder: " ) 
 backtrackingOrder ( btree , fn _ { } , fn _ { } , fn v { print ( " " , v ) } ) 
 println ( ) 

 print ( "level-order:" ) 
 levelOrder ( btree , fn v { print ( " " , v ) } ) 
 println ( )

[edit] Eiffel

Works with : EiffelStudio version 7.3, Void-Safety disabled

Void-Safety has been disabled for simplicity of the code.

 note 
 description : "Application for tree traversal demonstration" 
 output : "[ 
 Prints preorder, inorder, postorder and levelorder traversal of an example binary tree. 
 ]" 
 author : "Jascha Grübel" 
 date : "$2014-01-07$" 
 revision : "$1.0$" 

 class 
 APPLICATION 

 create 
 make 

 feature { NONE } -- Initialization 

 make 
 -- Run Tree traversal example. 
  local 
 tree : NODE 
 do 
 create tree. make ( 1 ) 
 tree. set_left_child ( create { NODE } . make ( 2 ) ) 
 tree. set_right_child ( create { NODE } . make ( 3 ) ) 
 tree. left_child . set_left_child ( create { NODE } . make ( 4 ) ) 
 tree. left_child . set_right_child ( create { NODE } . make ( 5 ) ) 
 tree. left_child . left_child . set_left_child ( create { NODE } . make ( 7 ) ) 
 tree. right_child . set_left_child ( create { NODE } . make ( 6 ) ) 
 tree. right_child . left_child . set_left_child ( create { NODE } . make ( 8 ) ) 
 tree. right_child . left_child . set_right_child ( create { NODE } . make ( 9 ) ) 

 Io. put_string ( "preorder: " ) 
 tree. print_preorder 
 Io. put_new_line 

 Io. put_string ( "inorder: " ) 
 tree. print_inorder 
 Io. put_new_line 

 Io. put_string ( "postorder: " ) 
 tree. print_postorder 
 Io. put_new_line 

 Io. put_string ( "level-order:" ) 
 tree. print_levelorder 
 Io. put_new_line 

  end 

 end -- class APPLICATION 
 note 
 description : "A simple node for a binary tree" 
 libraries : "Relies on LINKED_LIST from EiffelBase" 
 author : "Jascha Grübel" 
 date : "$2014-01-07$" 
 revision : "$1.0$" 
 implementation : "[ 
 All traversals but the levelorder traversal have been implemented recursively. 
 The levelorder traversal is solved iteratively. 
 ]" 

 class 
 NODE 
 create 
 make 

 feature { NONE } -- Initialization 

 make ( a_value : INTEGER ) 
 -- Creates a node with no children. 
 do 
 value := a_value 
 set_right_child ( Void ) 
 set_left_child ( Void ) 
  end 

 feature -- Modification 

 set_right_child ( a_node : NODE ) 
 -- Sets `right_child' to `a_node'. 
 do 
 right_child := a_node 
  end 

 set_left_child ( a_node : NODE ) 
 -- Sets `left_child' to `a_node'. 
 do 
 left_child := a_node 
  end 

 feature -- Representation 

 print_preorder 
 -- Recursively prints the value of the node and all its children in preorder 
 do 
 Io. put_string ( " " + value. out ) 
 if has_left_child then 
 left_child. print_preorder 
  end 
 if has_right_child then 
 right_child. print_preorder 
  end 
  end 

 print_inorder 
 -- Recursively prints the value of the node and all its children in inorder 
 do 
 if has_left_child then 
 left_child. print_inorder 
  end 
 Io. put_string ( " " + value. out ) 
 if has_right_child then 
 right_child. print_inorder 
  end 
  end 

 print_postorder 
 -- Recursively prints the value of the node and all its children in postorder 
 do 
 if has_left_child then 
 left_child. print_postorder 
  end 
 if has_right_child then 
 right_child. print_postorder 
  end 
 Io. put_string ( " " + value. out ) 
  end 

 print_levelorder 
 -- Iteratively prints the value of the node and all its children in levelorder 
  local 
 l_linked_list : LINKED_LIST [ NODE ] 
 l_node : NODE 
 do 
 from 
 create l_linked_list. make 
 l_linked_list. extend ( Current ) 
 until 
 l_linked_list. is_empty 
 loop 
 l_node := l_linked_list. first 
 if l_node. has_left_child then 
 l_linked_list. extend ( l_node. left_child ) 
  end 
 if l_node. has_right_child then 
 l_linked_list. extend ( l_node. right_child ) 
  end 
 Io. put_string ( " " + l_node. value . out ) 
 l_linked_list. prune ( l_node ) 
  end 
  end 

 feature -- Access 

 value : INTEGER 
 -- Value stored in the node. 

 right_child : NODE 
 -- Reference to right child, possibly void. 

 left_child : NODE 
 -- Reference to left child, possibly void. 

 has_right_child : BOOLEAN 
 -- Test right child for existence. 
 do 
 Result := right_child /= Void 
  end 

 has_left_child : BOOLEAN 
 -- Test left child for existence. 
 do 
 Result := left_child /= Void 
  end 

  end 
 -- class NODE

[edit] Elisa

This is a generic component for binary tree traversals. More information about binary trees in Elisa are given in trees.

 component BinaryTreeTraversals (Tree, Element); 
 type Tree; 
 type Node = Tree; 
 Tree (LeftTree = Tree, Element, RightTree = Tree) -> Tree; 
 Leaf (Element) -> Node; 
 Node (Tree) -> Node; 
 Item (Node) -> Element; 

 Preorder (Tree) -> multi (Node); 
 Inorder (Tree) -> multi (Node); 
 Postorder (Tree) -> multi (Node); 
 Level_order(Tree) -> multi (Node); 
  begin 
 Tree (Lefttree, Item, Righttree) = Tree: [ Lefttree; Item; Righttree ]; 
 Leaf (anItem) = Tree (null(Tree), anItem, null(Tree) ); 
 Node (aTree) = aTree; 
 Item (aNode) = aNode.Item; 

 Preorder (=null(Tree)) = no(Tree); 
 Preorder (T) = ( T, Preorder (T.Lefttree), Preorder (T.Righttree)); 

 Inorder (=null(Tree)) = no(Tree); 
 Inorder (T) = ( Inorder (T.Lefttree), T, Inorder (T.Righttree)); 

 Postorder (=null(Tree)) = no(Tree); 
 Postorder (T) = ( Postorder (T.Lefttree), Postorder (T.Righttree), T); 

 Level_order(T) = [ Queue = {T}; 
 node = Tree:items(Queue); 
 [ result(node); 
 add(Queue, node.Lefttree) when valid(node.Lefttree); 
 add(Queue, node.Righttree) when valid(node.Righttree); 
  ]; 
 no(Tree); 
  ]; 
 end component BinaryTreeTraversals;

Tests

 use BinaryTreeTraversals (Tree, integer); 

 BT = Tree( 
 Tree( 
 Tree(Leaf(7), 4, null(Tree)), 2 , Leaf(5)), 1, 
 Tree( 
 Tree(Leaf(8), 6, Leaf(9)), 3 ,null(Tree))); 

 {Item(Preorder(BT))}? 
 { 1, 2, 4, 7, 5, 3, 6, 8, 9} 

 {Item(Inorder(BT))}? 
 { 7, 4, 2, 5, 1, 8, 6, 9, 3} 

 {Item(Postorder(BT))}? 
 { 7, 4, 5, 2, 8, 9, 6, 3, 1} 

 {Item(Level_order(BT))}? 
 { 1, 2, 3, 4, 5, 6, 7, 8, 9}

[edit] Erlang

 - module ( tree_traversal ) . 
 - export ( [ main / 0 ] ) . 
 - export ( [ preorder / 2 , inorder / 2 , postorder / 2 , levelorder / 2 ] ) . 
 - export ( [ tnode / 0 , tnode / 1 , tnode / 3 ] ) . 

 - define ( NEWLINE , io : format ( "~n" ) ) . 

 tnode ( ) -> { } . 
 tnode ( V ) -> { node , V , { } , { } } . 
 tnode ( V , L , R ) -> { node , V , L , R } . 

 preorder ( _ , { } ) -> ok ; 
 preorder ( F , { node , V , L , R } ) -> 
 F ( V ) , preorder ( F , L ) , preorder ( F , R ) . 

 inorder ( _ , { } ) -> ok ; 
 inorder ( F , { node , V , L , R } ) -> 
 inorder ( F , L ) , F ( V ) , inorder ( F , R ) . 

 postorder ( _ , { } ) -> ok ; 
 postorder ( F , { node , V , L , R } ) -> 
 postorder ( F , L ) , postorder ( F , R ) , F ( V ) . 

 levelorder ( _ , [ ] ) -> [ ] ; 
 levelorder ( F , [ { } |T ] ) -> levelorder ( F , T ) ; 
 levelorder ( F , [ { node , V , L , R } |T ] ) -> 
 F ( V ) , levelorder ( F , T ++ [ L , R ] ) ; 
 levelorder ( F , X ) -> levelorder ( F , [ X ] ) . 

 main ( ) -> 
 Tree = tnode ( 1 , 
 tnode ( 2 , 
 tnode ( 4 , tnode ( 7 ) , tnode ( ) ) , 
 tnode ( 5 , tnode ( ) , tnode ( ) ) ) , 
 tnode ( 3 , 
 tnode ( 6 , tnode ( 8 ) , tnode ( 9 ) ) , 
 tnode ( ) ) ) , 
 F = fun ( X ) -> io : format ( "~p " , [ X ] ) end , 
 preorder ( F , Tree ) , ? NEWLINE , 
 inorder ( F , Tree ) , ? NEWLINE , 
 postorder ( F , Tree ) , ? NEWLINE , 
 levelorder ( F , Tree ) , ? NEWLINE .

Output:

 1 2 4 7 5 3 6 8 9 
7 4 2 5 1 8 6 9 3 
7 4 5 2 8 9 6 3 1 
1 2 3 4 5 6 7 8 9

[edit] Euphoria

 constant VALUE = 1 , LEFT = 2 , RIGHT = 3 

 constant tree = { 1 , 
 { 2 , 
 { 4 , 
 { 7 , 0 , 0 } , 
 0 } , 
 { 5 , 0 , 0 } } , 
 { 3 , 
 { 6 , 
 { 8 , 0 , 0 } , 
 { 9 , 0 , 0 } } , 
 0 } } 

 procedure preorder ( object tree ) 
 if sequence ( tree ) then 
 printf ( 1 , "%d " , { tree [ VALUE ] } ) 
 preorder ( tree [ LEFT ] ) 
 preorder ( tree [ RIGHT ] ) 
 end if 
 end procedure 

 procedure inorder ( object tree ) 
 if sequence ( tree ) then 
 inorder ( tree [ LEFT ] ) 
 printf ( 1 , "%d " , { tree [ VALUE ] } ) 
 inorder ( tree [ RIGHT ] ) 
 end if 
 end procedure 

 procedure postorder ( object tree ) 
 if sequence ( tree ) then 
 postorder ( tree [ LEFT ] ) 
 postorder ( tree [ RIGHT ] ) 
 printf ( 1 , "%d " , { tree [ VALUE ] } ) 
 end if 
 end procedure 

 procedure lo ( object tree , sequence more ) 
 if sequence ( tree ) then 
 more &= { tree [ LEFT ] , tree [ RIGHT ] } 
 printf ( 1 , "%d " , { tree [ VALUE ] } ) 
 end if 
 if length ( more ) > 0 then 
 lo ( more [ 1 ] , more [ 2 ..$ ] ) 
 end if 
 end procedure 

 procedure level_order ( object tree ) 
 lo ( tree , { } ) 
 end procedure 

 puts ( 1 , "preorder: " ) 
 preorder ( tree ) 
 puts ( 1 , ' \n ' ) 

 puts ( 1 , "inorder: " ) 
 inorder ( tree ) 
 puts ( 1 , ' \n ' ) 

 puts ( 1 , "postorder: " ) 
 postorder ( tree ) 
 puts ( 1 , ' \n ' ) 

 puts ( 1 , "level-order: " ) 
 level_order ( tree ) 
 puts ( 1 , ' \n ' )

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
level-order: 1 2 3 4 5 6 7 8 9

[edit] F#

 open System 
 open System. IO 

 type Tree < 'a> = 
  | Tree of ' a * Tree < 'a> * Tree<' a > 
  |  Empty 

 let rec inorder tree = 
 seq { 
 match tree with 
  | Tree ( x, left, right ) -> 
 yield! inorder left 
 yield x 
 yield! inorder right 
  | Empty -> ( ) 
  } 

 let rec preorder tree = 
 seq { 
 match tree with 
  | Tree ( x, left, right ) -> 
 yield x 
 yield! preorder left 
 yield! preorder right 
  | Empty -> ( ) 
  } 

 let rec postorder tree = 
 seq { 
 match tree with 
  | Tree ( x, left, right ) -> 
 yield! postorder left 
 yield! postorder right 
 yield x 
  | Empty -> ( ) 
  } 

 let levelorder tree = 
 let rec loop queue = 
 seq { 
 match queue with 
  | [ ] -> ( ) 
  | ( Empty::tail ) -> yield! loop tail 
  | ( Tree ( x, l, r ) ::tail ) -> 
 yield x 
 yield! loop ( tail @ [ l ; r ] ) 
  } 
 loop [ tree ] 

 [ < EntryPoint > ] 
 let main _ = 
 let tree = 
 Tree ( 1 , 
 Tree ( 2 , 
 Tree ( 4 , 
 Tree ( 7 , Empty, Empty ) , 
 Empty ) , 
 Tree ( 5 , Empty, Empty ) ) , 
 Tree ( 3 , 
 Tree ( 6 , 
 Tree ( 8 , Empty, Empty ) , 
 Tree ( 9 , Empty, Empty ) ) , 
 Empty ) ) 

 let show x = printf "%d " x 

 printf "preorder: " 
 preorder tree |> Seq . iter show 
 printf " \n inorder: " 
 inorder tree |> Seq . iter show 
 printf " \n postorder: " 
 postorder tree |> Seq . iter show 
 printf " \n level-order: " 
 levelorder tree |> Seq . iter show 
  0

[edit] Factor

 USING: accessors combinators deques dlists fry io kernel 
 math.parser ; 
 IN: rosetta.tree-traversal 

 TUPLE: node data left right ; 

 CONSTANT: example-tree 
 T{ node f 1 
 T{ node f 2 
 T{ node f 4 
 T{ node f 7 ff } 
  f 
  } 
 T{ node f 5 ff } 
  } 
 T{ node f 3 
 T{ node f 6 
 T{ node f 8 ff } 
 T{ node f 9 ff } 
  } 
  f 
  } 
  } 

 : preorder ( node quot: ( data -- ) -- ) 
 [ [ data>> ] dip call ] 
 [ [ left>> ] dip over [ preorder ] [ 2drop ] if ] 
 [ [ right>> ] dip over [ preorder ] [ 2drop ] if ] 
 2tri ; inline recursive 

 : inorder ( node quot: ( data -- ) -- ) 
 [ [ left>> ] dip over [ inorder ] [ 2drop ] if ] 
 [ [ data>> ] dip call ] 
 [ [ right>> ] dip over [ inorder ] [ 2drop ] if ] 
 2tri ; inline recursive 

 : postorder ( node quot: ( data -- ) -- ) 
 [ [ left>> ] dip over [ postorder ] [ 2drop ] if ] 
 [ [ right>> ] dip over [ postorder ] [ 2drop ] if ] 
 [ [ data>> ] dip call ] 
 2tri ; inline recursive 

 : (levelorder) ( dlist quot: ( data -- ) -- ) 
 over deque-empty? [ 2drop ] [ 
 [ dup pop-front ] dip { 
 [ [ data>> ] dip call drop ] 
 [ drop left>> [ swap push-back ] [ drop ] if* ] 
 [ drop right>> [ swap push-back ] [ drop ] if* ] 
 [ nip (levelorder) ] 
 } 3cleave 
 ] if ; inline recursive 

 : levelorder ( node quot: ( data -- ) -- ) 
 [ 1dlist ] dip (levelorder) ; inline 

 : levelorder2 ( node quot: ( data -- ) -- ) 
 [ 1dlist ] dip 
 [ dup deque-empty? not ] swap '[ 
 dup pop-front 
 [ data>> @ ] 
 [ left>> [ over push-back ] when* ] 
 [ right>> [ over push-back ] when* ] tri 
 ] while drop ; inline 

 : main ( -- ) 
 example-tree [ number>string write " " write ] { 
 [ "preorder: " write preorder nl ] 
 [ "inorder: " write inorder nl ] 
 [ "postorder: " write postorder nl ] 
 [ "levelorder: " write levelorder nl ] 
 [ "levelorder2: " write levelorder2 nl ] 
 } 2cleave ;

[edit] Fantom

 class Tree 
  { 
 readonly Int label 
 readonly Tree?  left 
 readonly Tree?  right 

 new make (Int label, Tree? left := null, Tree? right := null) 
  { 
 this.label = label 
 this.left = left 
 this.right = right 
  } 

 Void preorder(|Int->Void| func) 
  { 
 func(label) 
 left?.preorder(func) // ?. will not call method if 'left' is null 
 right?.preorder(func) 
  } 

 Void postorder(|Int->Void| func) 
  { 
 left?.postorder(func) 
 right?.postorder(func) 
 func(label) 
  } 

 Void inorder(|Int->Void| func) 
  { 
 left?.inorder(func) 
 func(label) 
 right?.inorder(func) 
  } 

 Void levelorder(|Int->Void| func) 
  { 
 Tree[] nodes := [this] 
 while (nodes.size > 0) 
  { 
 Tree cur := nodes.removeAt(0) 
 func(cur.label) 
 if (cur.left != null) nodes.add (cur.left) 
 if (cur.right != null) nodes.add (cur.right) 
  } 
  } 
  } 

 class Main 
  { 
 public static Void main () 
  { 
 tree := Tree(1, 
 Tree(2, Tree(4, Tree(7)), Tree(5)), 
 Tree(3, Tree(6, Tree(8), Tree(9)))) 
 List result := [,] 
 collect := |Int a -> Void| { result.add(a) } 
 tree.preorder(collect) 
 echo ("preorder: " + result.join(" ")) 
 result = [,] 
 tree.inorder(collect) 
 echo ("inorder: " + result.join(" ")) 
 result = [,] 
 tree.postorder(collect) 
 echo ("postorder: " + result.join(" ")) 
 result = [,] 
 tree.levelorder(collect) 
 echo ("levelorder: " + result.join(" ")) 
  } 
  }

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
levelorder: 1 2 3 4 5 6 7 8 9

[edit] Forth

 \ binary tree (dictionary) 
 : node ( lr data -- node ) here >r , , , r> ; 
 : leaf ( data -- node ) 0 0 rot node ; 

 : >data ( node -- ) @ ; 
 : >right ( node -- ) cell+ @ ; 
 : >left ( node -- ) cell+ cell+ @ ; 

 : preorder ( xt tree -- ) 
 dup 0= if 2drop exit then 
 2dup >data swap execute 
 2dup >left recurse 
 >right recurse ; 

 : inorder ( xt tree -- ) 
 dup 0= if 2drop exit then 
 2dup >left recurse 
 2dup >data swap execute 
 >right recurse ; 

 : postorder ( xt tree -- ) 
 dup 0= if 2drop exit then 
 2dup >left recurse 
 2dup >right recurse 
 >data swap execute ; 

 : max-depth ( tree -- n ) 
 dup 0= if exit then 
 dup >left recurse 
 swap >right recurse max 1+ ; 

 defer depthaction 
 : depthorder ( depth tree -- ) 
 dup 0= if 2drop exit then 
 over 0= 
 if >data depthaction drop 
 else over 1- over >left recurse 
 swap 1- swap >right recurse 
 then ; 

 : levelorder ( xt tree -- ) 
 swap is depthaction 
 dup max-depth 0 ?do 
 i over depthorder 
 loop drop ; 

 7 leaf 0 4 node 
 5 leaf 2 node 
 8 leaf 9 leaf 6 node 
 0 3 node 1 node value tree 

 cr ' . tree preorder \ 1 2 4 7 5 3 6 8 9 
 cr ' . tree inorder \ 7 4 2 5 1 8 6 9 3 
 cr ' . tree postorder \ 7 4 5 2 8 9 6 3 1 
 cr tree max-depth . \ 4 
 cr ' . tree levelorder \ 1 2 3 4 5 6 7 8 9

[edit] FunL

Translation of : Haskell
 data Tree = Empty | Node( value, left, right ) 

 def 
 preorder( Empty ) = [] 
 preorder( Node(v, l, r) ) = [v] + preorder( l ) + preorder( r ) 

 inorder( Empty ) = [] 
 inorder( Node(v, l, r) ) = inorder( l ) + [v] + inorder( r ) 

 postorder( Empty ) = [] 
 postorder( Node(v, l, r) ) = postorder( l ) + postorder( r ) + [v] 

 levelorder( x ) = 
 def 
 order( [] ) = [] 
 order( Empty  : xs ) = order( xs ) 
 order( Node(v, l, r) : xs ) = v : order( xs + [l, r] ) 

 order( [x] ) 

 tree = Node( 1, 
 Node( 2, 
 Node( 4, 
 Node( 7, Empty, Empty ), 
 Empty ), 
 Node( 5, Empty, Empty ) ), 
 Node( 3, 
 Node( 6, 
 Node( 8, Empty, Empty ), 
 Node( 9, Empty, Empty ) ), 
 Empty ) ) 

 println( preorder(tree) ) 
 println( inorder(tree) ) 
 println( postorder(tree) ) 
 println( levelorder(tree) )

Output:

 [1, 2, 4, 7, 5, 3, 6, 8, 9]
[7, 4, 2, 5, 1, 8, 6, 9, 3]
[7, 4, 5, 2, 8, 9, 6, 3, 1]
[1, 2, 3, 4, 5, 6, 7, 8, 9]

[edit] Go

[edit] Individually allocated nodes

Translation of : C

This is like many examples on this page.

 package main 

 import "fmt" 

 type node struct { 
 value int 
 left , right * node 
  } 

 func ( n * node ) iterPreorder ( visit func ( int )) { 
 if n == nil { 
 return 
  } 
 visit ( n . value ) 
 n . left . iterPreorder ( visit ) 
 n . right . iterPreorder ( visit ) 
  } 

 func ( n * node ) iterInorder ( visit func ( int )) { 
 if n == nil { 
 return 
  } 
 n . left . iterInorder ( visit ) 
 visit ( n . value ) 
 n . right . iterInorder ( visit ) 
  } 

 func ( n * node ) iterPostorder ( visit func ( int )) { 
 if n == nil { 
 return 
  } 
 n . left . iterPostorder ( visit ) 
 n . right . iterPostorder ( visit ) 
 visit ( n . value ) 
  } 

 func ( n * node ) iterLevelorder ( visit func ( int )) { 
 if n == nil { 
 return 
  } 
 for queue := [] * node { n };  ;  { 
 n = queue [ 0 ] 
 visit ( n . value ) 
 copy ( queue , queue [ 1 :]) 
 queue = queue [: len ( queue ) - 1 ] 
 if n . left != nil { 
 queue = append ( queue , n . left ) 
  } 
 if n . right != nil { 
 queue = append ( queue , n . right ) 
  } 
 if len ( queue ) == 0 { 
 return 
  } 
  } 
  } 

 func main () { 
 tree := &node { 1 , 
 &node { 2 , 
 &node { 4 , 
 &node { 7 , nil , nil }, 
 nil }, 
 &node { 5 , nil , nil }}, 
 &node { 3 , 
 &node { 6 , 
 &node { 8 , nil , nil }, 
 &node { 9 , nil , nil }}, 
 nil }} 
 fmt . Print ( "preorder: " ) 
 tree . iterPreorder ( visitor ) 
 fmt . Println () 
 fmt . Print ( "inorder: " ) 
 tree . iterInorder ( visitor ) 
 fmt . Println () 
 fmt . Print ( "postorder: " ) 
 tree . iterPostorder ( visitor ) 
 fmt . Println () 
 fmt . Print ( "level-order: " ) 
 tree . iterLevelorder ( visitor ) 
 fmt . Println () 
  } 

 func visitor ( value int ) { 
 fmt . Print ( value , " " ) 
  }

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
level-order: 1 2 3 4 5 6 7 8 9

[edit] Flat slice

Alternative representation. Like Wikipedia Binary tree#Arrays

 package main 

 import "fmt" 

 // flat, level-order representation. 
 // for node at index k, left child has index 2k, right child has index 2k+1. 
 // a value of -1 means the node does not exist. 
 type tree [] int 

 func main () { 
 t := tree { 1 , 2 , 3 , 4 , 5 , 6 , - 1 , 7 , - 1 , - 1 , - 1 , 8 , 9 } 
 visitor := func ( n int ) { 
 fmt . Print ( n , " " ) 
  } 
 fmt . Print ( "preorder: " ) 
 t . iterPreorder ( visitor ) 
 fmt . Print ( " \n inorder: " ) 
 t . iterInorder ( visitor ) 
 fmt . Print ( " \n postorder: " ) 
 t . iterPostorder ( visitor ) 
 fmt . Print ( " \n level-order: " ) 
 t . iterLevelorder ( visitor ) 
 fmt . Println () 
  } 

 func ( t tree ) iterPreorder ( visit func ( int )) { 
 var traverse func ( int ) 
 traverse = func ( k int ) { 
 if k > = len ( t ) || t [ k ] == - 1 { 
 return 
  } 
 visit ( t [ k ]) 
 traverse ( 2 * k + 1 ) 
 traverse ( 2 * k + 2 ) 
  } 
 traverse ( 0 ) 
  } 

 func ( t tree ) iterInorder ( visit func ( int )) { 
 var traverse func ( int ) 
 traverse = func ( k int ) { 
 if k > = len ( t ) || t [ k ] == - 1 { 
 return 
  } 
 traverse ( 2 * k + 1 ) 
 visit ( t [ k ]) 
 traverse ( 2 * k + 2 ) 
  } 
 traverse ( 0 ) 
  } 

 func ( t tree ) iterPostorder ( visit func ( int )) { 
 var traverse func ( int ) 
 traverse = func ( k int ) { 
 if k > = len ( t ) || t [ k ] == - 1 { 
 return 
  } 
 traverse ( 2 * k + 1 ) 
 traverse ( 2 * k + 2 ) 
 visit ( t [ k ]) 
  } 
 traverse ( 0 ) 
  } 

 func ( t tree ) iterLevelorder ( visit func ( int )) { 
 for _ , n := range t { 
 if n != - 1 { 
 visit ( n ) 
  } 
  } 
  }

[edit] Groovy

Uses Groovy Node and NodeBuilder classes

 def preorder ; 
 preorder = { Node node -> 
 ( [ node ] + node. children ( ) . collect { preorder ( it ) } ) . flatten ( ) 
  } 

 def postorder ; 
 postorder = { Node node -> 
 ( node. children ( ) . collect { postorder ( it ) } + [ node ] ) . flatten ( ) 
  } 

 def inorder ; 
 inorder = { Node node -> 
 def kids = node. children ( ) 
 if ( kids. empty ) [ node ] 
 else if ( kids. size ( ) == 1 && kids [ 0 ] . '@right' ) [ node ] + inorder ( kids [ 0 ] ) 
 else inorder ( kids [ 0 ] ) + [ node ] + ( kids. size ( ) > 1 ? inorder ( kids [ 1 ] ) : [ ] ) 
  } 

 def levelorder = { Node node -> 
 def nodeList = [ ] 
 def level = [ node ] 
 while ( ! level. empty ) { 
 nodeList += level 
 def nextLevel = level. collect { it. children ( ) } . flatten ( ) 
 level = nextLevel 
  } 
 nodeList 
  } 

 class BinaryNodeBuilder extends NodeBuilder { 
 protected Object postNodeCompletion ( Object parent, Object node ) { 
 assert node. children ( ) . size ( ) < 3 
 node 
  } 
  }

Verify that BinaryNodeBuilder will not allow a node to have more than 2 children

 try { 
 new BinaryNodeBuilder ( ) . '1' { 
 a { } 
 b { } 
 c { } 
  } 
 println 'not limited to binary tree \r \n ' 
 } catch ( org. codehaus . groovy . transform . powerassert . PowerAssertionError e ) { 
 println 'limited to binary tree \r \n ' 
  }

Test case #1 (from the task definition)

 // 1 
 // / \ 
 // 2 3 
 // / \ / 
 // 4 5 6 
 // / / \ 
 // 7 8 9 
 def tree1 = new BinaryNodeBuilder ( ) . 
 '1' { 
 '2' { 
 '4' { '7' { } } 
 '5' { } 
  } 
 '3' { 
 '6' { '8' { } ; '9' { } } 
  } 
  }

Test case #2 (tests single right child)

 // 1 
 // / \ 
 // 2 3 
 // / \ / 
 // 4 5 6 
 // \ / \ 
 // 7 8 9 
 def tree2 = new BinaryNodeBuilder ( ) . 
 '1' { 
 '2' { 
 '4' { '7' ( right: true ) { } } 
 '5' { } 
  } 
 '3' { 
 '6' { '8' { } ; '9' { } } 
  } 
  }

Run tests:

 def test = { tree -> 
 println "preorder: ${preorder(tree).collect{it.name()}}" 
 println "preorder: ${tree.depthFirst().collect{it.name()}}" 

 println "postorder: ${postorder(tree).collect{it.name()}}" 

 println "inorder: ${inorder(tree).collect{it.name()}}" 

 println "level-order: ${levelorder(tree).collect{it.name()}}" 
 println "level-order: ${tree.breadthFirst().collect{it.name()}}" 

 println ( ) 
  } 
 test ( tree1 ) 
 test ( tree2 )

Output:

 limited to binary tree

preorder: [1, 2, 4, 7, 5, 3, 6, 8, 9]
preorder: [1, 2, 4, 7, 5, 3, 6, 8, 9]
postorder: [7, 4, 5, 2, 8, 9, 6, 3, 1]
inorder: [7, 4, 2, 5, 1, 8, 6, 9, 3]
level-order: [1, 2, 3, 4, 5, 6, 7, 8, 9]
level-order: [1, 2, 3, 4, 5, 6, 7, 8, 9]

preorder: [1, 2, 4, 7, 5, 3, 6, 8, 9]
preorder: [1, 2, 4, 7, 5, 3, 6, 8, 9]
postorder: [7, 4, 5, 2, 8, 9, 6, 3, 1]
inorder: [4, 7, 2, 5, 1, 8, 6, 9, 3]
level-order: [1, 2, 3, 4, 5, 6, 7, 8, 9]
level-order: [1, 2, 3, 4, 5, 6, 7, 8, 9]

[edit] Haskell

 data Tree a = Empty 
  | Node { value :: a , 
 left :: Tree a , 
 right :: Tree a } 

 preorder , inorder , postorder , levelorder :: Tree a -> [ a ] 

 preorder Empty = [ ] 
 preorder ( Node vlr ) = [ v ] 
 ++ preorder l 
 ++ preorder r 

 inorder Empty = [ ] 
 inorder ( Node vlr ) = inorder l 
 ++ [ v ] 
 ++ inorder r 

 postorder Empty = [ ] 
 postorder ( Node vlr ) = postorder l 
 ++ postorder r 
 ++ [ v ] 

 levelorder x = loop [ x ] 
 where loop [ ] = [ ] 
 loop ( Empty  : xs ) = loop xs 
 loop ( Node vl r : xs ) = v : loop ( xs ++ [ l , r ] ) 

 tree :: Tree Int 
 tree = Node 1 
 ( Node 2 
 ( Node 4 
 ( Node 7 Empty Empty ) 
 Empty ) 
 ( Node 5 Empty Empty ) ) 
 ( Node 3 
 ( Node 6 
 ( Node 8 Empty Empty ) 
 ( Node 9 Empty Empty ) ) 
 Empty ) 

 main :: IO ( ) 
 main = do print $ preorder tree 
 print $ inorder tree 
 print $ postorder tree 
 print $ levelorder tree

Output:

 [1,2,4,7,5,3,6,8,9]
[7,4,2,5,1,8,6,9,3]
[7,4,5,2,8,9,6,3,1]
[1,2,3,4,5,6,7,8,9]

[edit] Icon and Unicon

 procedure main ( ) 
 bTree := [ 1 , [ 2 , [ 4 , [ 7 ] ] , [ 5 ] ] , [ 3 , [ 6 , [ 8 ] , [ 9 ] ] ] ] 
 showTree ( bTree , preorder | inorder | postorder | levelorder ) 
  end 

 procedure showTree ( tree , f ) 
 writes ( image ( f ) , ": \t " ) 
 every writes ( " " , f ( tree ) [ 1 ] ) 
 write ( ) 
  end 

 procedure preorder ( L ) 
 if \ L then suspend L | preorder ( L [ 2 | 3 ] ) 
  end 

 procedure inorder ( L ) 
 if \ L then suspend inorder ( L [ 2 ] ) | L | inorder ( L [ 3 ] ) 
  end 

 procedure postorder ( L ) 
 if \ L then suspend postorder ( L [ 2 | 3 ] ) |  L 
  end 

 procedure levelorder ( L ) 
 if \ L then { 
 queue := [ L ] 
 while nextnode := get ( queue ) do { 
 every put ( queue , \ nextnode [ 2 | 3 ] ) 
 suspend nextnode 
  } 
  } 
  end

Output:

 ->bintree
procedure preorder: 1 2 4 7 5 3 6 8 9
procedure inorder: 7 4 2 5 1 8 6 9 3
procedure postorder: 7 4 5 2 8 9 6 3 1
procedure levelorder: 1 2 3 4 5 6 7 8 9
 ->

[edit] J

 preorder=: ]S: 0 
 postorder=: ( [:; postorder&.>@}. ) , >@{. 
 levelorder=: ;@ ( {::L: 1 _ ~ [: ( /: #@> ) 1 @{:: ) 
 inorder=: ( [:; inorder&.>@ ( '' " _ ` ( 1 &{ ) @. ( 1 <# ))) , >@{. , [:; inorder&.>@}.@}.

Required example:

 N2=: conjunction def '( 
 N1=: adverb def '( 
 L=: adverb def ' 

 tree=: 1 N2 ( 2 N2 ( 4 N1 ( 7 L )) 5 L ) 3 N1 6 N2 ( 8 L ) 9 L

This tree is organized in a pre-order fashion

 preorder tree 
 1 2 4 7 5 3 6 8 9

post-order is not that much different from pre-order, except that the children must extracted before the parent.

 postorder tree 
 7 4 5 2 8 9 6 3 1

Implementing in-order is more complex because we must sometimes test whether we have any leaves, instead of relying on J's implicit looping over lists

 inorder tree 
 7 4 2 5 1 8 6 9 3

level-order can be accomplished by constructing a map of the locations of the leaves, sorting these map locations by their non-leaf indices and using the result to extract all leaves from the tree. Elements at the same level with the same parent will have the same sort keys and thus be extracted in preorder fashion, which works just fine.

 levelorder tree 
  1 2 3 4 5 6 7 8 9


For J novices, here's the tree instance with a few redundant parenthesis:

 tree=: 1 N2 ( 2 N2 ( 4 N1 ( 7 L )) ( 5 L )) ( 3 N1 ( 6 N2 ( 8 L ) ( 9 L )))

Syntactically, N2 is a binary node expressed as m N2 ny . N1 is a node with a single child, expressed as m N2 y . L is a leaf node, expressed as m L . In all three cases, the parent value ( m ) for the node appears on the left, and the child tree(s) appear on the right. (And n must be parenthesized if it is not a single word.)

[edit] Java

Works with : Java version 1.5+
 import java.util.Queue ; 
 import java.util.LinkedList ; 
 public class TreeTraverse 
  { 
 private static class Node < T > 
  { 
 public Node < T > left ; 
 public Node < T > right ; 
 public T data ; 
 public Node ( T data ) 
  { 
 this . data = data ; 
  } 
 public Node < T > getLeft ( ) 
  { 
 return this . left ; 
  } 
 public void setLeft ( Node < T > left ) 
  { 
 this . left = left ; 
  } 
 public Node < T > getRight ( ) 
  { 
 return this . right ; 
  } 
 public void setRight ( Node < T > right ) 
  { 
 this . right = right ; 
  } 
  } 
 public static void preorder ( Node  n ) 
  { 
 if ( n ! = null ) 
  { 
 System . out . print ( n. data + " " ) ; 
 preorder ( n. getLeft ( ) ) ; 
 preorder ( n. getRight ( ) ) ; 
  } 
  } 
 public static void inorder ( Node  n ) 
  { 
 if ( n ! = null ) 
  { 
 inorder ( n. getLeft ( ) ) ; 
 System . out . print ( n. data + " " ) ; 
 inorder ( n. getRight ( ) ) ; 
  } 
  } 
 public static void postorder ( Node  n ) 
  { 
 if ( n ! = null ) 
  { 
 postorder ( n. getLeft ( ) ) ; 
 postorder ( n. getRight ( ) ) ; 
 System . out . print ( n. data + " " ) ; 
  } 
  } 
 public static void levelorder ( Node  n ) 
  { 
 Queue < Node > nodequeue = new LinkedList < Node > ( ) ; 
 if ( n ! = null ) 
 nodequeue. add ( n ) ; 
 while ( ! nodequeue. isEmpty ( ) ) 
  { 
 Node  next = nodequeue. remove ( ) ; 
 System . out . print ( next. data + " " ) ; 
 if ( next. getLeft ( ) ! = null ) 
  { 
 nodequeue. add ( next. getLeft ( ) ) ; 
  } 
 if ( next. getRight ( ) ! = null ) 
  { 
 nodequeue. add ( next. getRight ( ) ) ; 
  } 
  } 
  } 
 public static void main ( final String [ ] args ) 
  { 
 Node < Integer > one = new Node < Integer > ( 1 ) ; 
 Node < Integer > two = new Node < Integer > ( 2 ) ; 
 Node < Integer > three = new Node < Integer > ( 3 ) ; 
 Node < Integer > four = new Node < Integer > ( 4 ) ; 
 Node < Integer > five = new Node < Integer > ( 5 ) ; 
 Node < Integer > six = new Node < Integer > ( 6 ) ; 
 Node < Integer > seven = new Node < Integer > ( 7 ) ; 
 Node < Integer > eight = new Node < Integer > ( 8 ) ; 
 Node < Integer > nine = new Node < Integer > ( 9 ) ; 
 one. setLeft ( two ) ; 
 one. setRight ( three ) ; 
 two. setLeft ( four ) ; 
 two. setRight ( five ) ; 
 three. setLeft ( six ) ; 
 four. setLeft ( seven ) ; 
 six. setLeft ( eight ) ; 
 six. setRight ( nine ) ; 
 preorder ( one ) ; 
 System . out . println ( ) ; 
 inorder ( one ) ; 
 System . out . println ( ) ; 
 postorder ( one ) ; 
 System . out . println ( ) ; 
 levelorder ( one ) ; 
 System . out . println ( ) ; 
  } 
  }

Output:

 1 2 4 7 5 3 6 8 9 
7 4 2 5 1 8 6 9 3 
7 4 5 2 8 9 6 3 1 
1 2 3 4 5 6 7 8 9

[edit] JavaScript

inspired by Ruby

 function BinaryTree ( value , left , right ) { 
 this . value = value ; 
 this . left = left ; 
 this . right = right ; 
  } 
 BinaryTree. prototype . preorder = function ( f ) { this . walk ( f , [ 'this' , 'left' , 'right' ] ) } 
 BinaryTree. prototype . inorder = function ( f ) { this . walk ( f , [ 'left' , 'this' , 'right' ] ) } 
 BinaryTree. prototype . postorder = function ( f ) { this . walk ( f , [ 'left' , 'right' , 'this' ] ) } 
 BinaryTree. prototype . walk = function ( func , order ) { 
 for ( var i in order ) 
 switch ( order [ i ] ) { 
 case "this" : func ( this . value ) ; break ; 
 case "left" : if ( this . left ) this . left . walk ( func , order ) ; break ; 
 case "right" : if ( this . right ) this . right . walk ( func , order ) ; break ; 
  } 
  } 
 BinaryTree. prototype . levelorder = function ( func ) { 
 var queue = [ this ] ; 
 while ( queue. length != 0 ) { 
 var node = queue. shift ( ) ; 
 func ( node. value ) ; 
 if ( node. left ) queue. push ( node. left ) ; 
 if ( node. right ) queue. push ( node. right ) ; 
  } 
  } 

 // convenience function for creating a binary tree 
 function createBinaryTreeFromArray ( ary ) { 
 var left = null , right = null ; 
 if ( ary [ 1 ] ) left = createBinaryTreeFromArray ( ary [ 1 ] ) ; 
 if ( ary [ 2 ] ) right = createBinaryTreeFromArray ( ary [ 2 ] ) ; 
 return new BinaryTree ( ary [ 0 ] , left , right ) ; 
  } 

 var tree = createBinaryTreeFromArray ( [ 1 , [ 2 , [ 4 , [ 7 ] ] , [ 5 ] ] , [ 3 , [ 6 , [ 8 ] , [ 9 ] ] ] ] ) ; 

 print ( "*** preorder ***" ) ; tree. preorder ( print ) ; 
 print ( "*** inorder ***" ) ; tree. inorder ( print ) ; 
 print ( "*** postorder ***" ) ; tree. postorder ( print ) ; 
 print ( "*** levelorder ***" ) ; tree. levelorder ( print ) ;

[edit] jq

All the ordering filters defined here produce streams. For the final output, each stream is condensed into an array.

The implementation assumes an array structured recursively as [ node, left, right ], where "left" and "right" may be [] or null equivalently.

 def preorder: 
 if length == 0 then empty 
 else .[0], (.[1]|preorder), (.[2]|preorder) 
  end; 

 def inorder: 
 if length == 0 then empty 
 else (.[1]|inorder), .[0] , (.[2]|inorder) 
  end; 

 def postorder: 
 if length == 0 then empty 
 else (.[1] | postorder), (.[2]|postorder), .[0] 
  end; 

 # Helper functions for levelorder: 
 # Produce a stream of the first elements 
 def heads: map( .[0] | select(. != null)) | .[]; 

 # Produce a stream of the left/right branches: 
 def tails: 
 if length == 0 then empty 
 else [map ( .[1], .[2] ) | .[] | select( . != null)] 
  end; 

 def levelorder: [.] | recurse( tails ) | heads;

The task :

 def task: 
 # [node, left, right] 
 def atree: [1, [2, [4, [7,[],[]], 
 []], 
 [5, [],[]]], 

 [3, [6, [8,[],[]], 
 [9,[],[]]], 
 []]] ; 

 "preorder: \( [atree|preorder ])", 
 "inorder: \( [atree|inorder ])", 
 "postorder: \( [atree|postorder ])", 
 "levelorder: \( [atree|levelorder])" 
  ; 

 task

Output:

 $ jq -n -c -r -f Tree_traversal.jq
preorder: [1,2,4,7,5,3,6,8,9]
inorder: [7,4,2,5,1,8,6,9,3]
postorder: [7,4,5,2,8,9,6,3,1]
levelorder: [1,2,3,4,5,6,7,8,9]

[edit] Julia

 tree = {1, {2, {4, {7,{},{}}, 
 {}}, 
 {5, {},{}}}, 
 {3, {6, {8,{},{}}, 
 {9,{},{}}}, 
 {}}} 

 preorder(t,f) = if !isempty(t) 
 f(t[1]) ; preorder(t[2],f) ; preorder(t[3],f) 
  end 

 inorder(t,f) = if !isempty(t) 
 inorder(t[2],f) ; f(t[1]) ; inorder(t[3],f) 
  end 

 postorder(t,f) = if !isempty(t) 
 postorder(t[2],f) ; postorder(t[3],f) ; f(t[1]) 
  end 

 levelorder(t,f) = while !isempty(t) 
 t = mapreduce(x->isa(x,Number)? (f(x);{}): x, vcat, t) 
  end

Output:

 julia> for f in {preorder, inorder, postorder, levelorder}
         f(tree, x->print(x," ")) ; println("<- $f")
        end
1 2 4 7 5 3 6 8 9 <- preorder
7 4 2 5 1 8 6 9 3 <- inorder
7 4 5 2 8 9 6 3 1 <- postorder
1 2 3 4 5 6 7 8 9 <- levelorder

[edit] Logo

  ; nodes are [data left right], use "first" to get data 

 to node.left :node 
 if empty? butfirst :node [output []] 
 output first butfirst :node 
  end 
 to node.right :node 
 if empty? butfirst :node [output []] 
 if empty? butfirst butfirst :node [output []] 
 output first butfirst butfirst :node 
  end 
 to max :a :b 
 output ifelse :a > :b [:a] [:b] 
  end 
 to tree.depth :tree 
 if empty? :tree [output 0] 
 output 1 + max tree.depth node.left :tree tree.depth node.right :tree 
  end 

 to pre.order :tree :action 
 if empty? :tree [stop] 
 invoke :action first :tree 
 pre.order node.left :tree :action 
 pre.order node.right :tree :action 
  end 
 to in.order :tree :action 
 if empty? :tree [stop] 
 in.order node.left :tree :action 
 invoke :action first :tree 
 in.order node.right :tree :action 
  end 
 to post.order :tree :action 
 if empty? :tree [stop] 
 post.order node.left :tree :action 
 post.order node.right :tree :action 
 invoke :action first :tree 
  end 
 to at.depth :n :tree :action 
 if empty? :tree [stop] 
 ifelse :n = 1 [invoke :action first :tree] [ 
 at.depth :n-1 node.left  :tree :action 
 at.depth :n-1 node.right :tree :action 
  ] 
  end 
 to level.order :tree :action 
 for [i 1 [tree.depth :tree]] [at.depth :i :tree :action] 
  end 

 make "tree [1 [2 [4 [7]] 
 [5]] 
 [3 [6 [8] 
 [9]]]] 

 pre.order :tree [(type ? "| |)] (print) 
 in.order :tree [(type ? "| |)] (print) 
 post.order :tree [(type ? "| |)] (print) 
 level.order :tree [(type ? "| |)] (print)

[edit] Logtalk

 :- object (tree_traversal). 

 :- public (orders / 1 ). 
 orders( Tree ) :- 
 write ( 'Pre-order: ' ), pre_order( Tree ), nl , 
 write ( 'In-order: ' ), in_order( Tree ), nl , 
 write ( 'Post-order: ' ), post_order( Tree ), nl , 
 write ( 'Level-order: ' ), level_order( Tree ). 

 :- public (orders / 0 ). 
 orders :- 
 tree( Tree ), 
 orders( Tree ). 

 tree( 
 t( 1 , 
 t( 2 , 
 t( 4 , 
 t( 7 , t, t), 
  t 
  ), 
 t( 5 , t, t) 
  ), 
 t( 3 , 
 t( 6 , 
 t( 8 , t, t), 
 t( 9 , t, t) 
  ), 
  t 
  ) 
  ) 
  ). 

 pre_order(t). 
 pre_order(t( Value , Left , Right )) :- 
 write ( Value ), write ( ' ' ), 
 pre_order( Left ), 
 pre_order( Right ). 

 in_order(t). 
 in_order(t( Value , Left , Right )) :- 
 in_order( Left ), 
 write ( Value ), write ( ' ' ), 
 in_order( Right ). 

 post_order(t). 
 post_order(t( Value , Left , Right )) :- 
 post_order( Left ), 
 post_order( Right ), 
 write ( Value ), write ( ' ' ). 

 level_order(t). 
 level_order(t( Value , Left , Right )) :- 
 % write tree root value 
 write ( Value ), write ( ' ' ), 
 % write rest of the tree 
 level_order([ Left , Right ], Tail - Tail ). 

 level_order([], Trees - []) :- 
 ( Trees \= [] -> 
 % print next level 
 level_order( Trees , Tail - Tail ) 
  ; % no more levels 
  true 
  ). 
 level_order([ Tree | Trees ], Rest0 ) :- 
 ( Tree = t( Value , Left , Right ) -> 
 write ( Value ), write ( ' ' ), 
 % collect the subtrees to print the next level 
 append( Rest0 , [ Left , Right | Tail ] - Tail , Rest1 ), 
 % continue printing the current level 
 level_order( Trees , Rest1 ) 
  ; % continue printing the current level 
 level_order( Trees , Rest0 ) 
  ). 

 % use difference-lists for constant time append 
 append( List1 - Tail1 , Tail1 - Tail2 , List1 - Tail2 ). 

 :- end_object .

Sample output:

  | ?- ?- tree_traversal::orders. 
 Pre-order: 1 2 4 7 5 3 6 8 9 
 In-order: 7 4 2 5 1 8 6 9 3 
 Post-order: 7 4 5 2 8 9 6 3 1 
 Level-order: 1 2 3 4 5 6 7 8 9 
  yes

[edit] Mathematica

 preorder[a_Integer] := a; 
 preorder[a_[b__]] := Flatten@{a, preorder /@ {b}}; 
 inorder[a_Integer] := a; 
 inorder[a_[b_, c_]] := Flatten@{inorder@b, a, inorder@c}; 
 inorder[a_[b_]] := Flatten@{inorder@b, a}; postorder[a_Integer] := a; 
 postorder[a_[b__]] := Flatten@{postorder /@ {b}, a}; 
 levelorder[a_] := 
 Flatten[Table[Level[a, {n}], {n, 0, Depth@a}]] /. {b_Integer[__] :> 
 b};

Example:

 preorder[1[2[4[7], 5], 3[6[8, 9]]]] 
 inorder[1[2[4[7], 5], 3[6[8, 9]]]] 
 postorder[1[2[4[7], 5], 3[6[8, 9]]]] 
 levelorder[1[2[4[7], 5], 3[6[8, 9]]]]

Output:

 {1, 2, 4, 7, 5, 3, 6, 8, 9}

{7, 4, 2, 5, 1, 8, 6, 9, 3}

{7, 4, 5, 2, 8, 9, 6, 3, 1}

{1, 2, 3, 4, 5, 6, 7, 8, 9}

[edit] Nimrod

 import queues, sequtils 

  type 
 Node[T] = ref TNode[T] 
 TNode[T] = object 
 data: T 
 left, right: Node[T] 

 proc newNode[T](data: T; left, right: Node[T] = nil): Node[T] = 
 Node[T](data: data, left: left, right: right) 

 proc preorder[T](n: Node[T]): seq[T] = 
 if n == nil: @[] 
 else: @[n.data] & preorder(n.left) & preorder(n.right) 

 proc inorder[T](n: Node[T]): seq[T] = 
 if n == nil: @[] 
 else: inorder(n.left) & @[n.data] & inorder(n.right) 

 proc postorder[T](n: Node[T]): seq[T] = 
 if n == nil: @[] 
 else: postorder(n.left) & postorder(n.right) & @[n.data] 

 proc levelorder[T](n: Node[T]): seq[T] = 
 result = @[] 
 var queue = initQueue[Node[T]]() 
 queue.enqueue(n) 
 while queue.len > 0: 
 let next = queue.dequeue() 
 result.add next.data 
 if next.left != nil: queue.enqueue(next.left) 
 if next.right != nil: queue.enqueue(next.right) 

 let tree = 1.newNode( 
 2.newNode( 
 4.newNode( 
 7.newNode), 
 5.newNode), 
 3.newNode( 
 6.newNode( 
 8.newNode, 
 9.newNode))) 

 echo preorder tree 
 echo inorder tree 
 echo postorder tree 
 echo levelorder tree

Output:

 @[1, 2, 4, 7, 5, 3, 6, 8, 9]
@[7, 4, 2, 5, 1, 8, 6, 9, 3]
@[7, 4, 5, 2, 8, 9, 6, 3, 1]
@[1, 2, 3, 4, 5, 6, 7, 8, 9]

[edit] Objeck

use Collection ; 

 class Test { 
 function : Main ( args : String [ ] ) ~ Nil { 
 one := Node -> New ( 1 ) ; 
 two := Node -> New ( 2 ) ; 
 three := Node -> New ( 3 ) ; 
 four := Node -> New ( 4 ) ; 
 five := Node -> New ( 5 ) ; 
 six := Node -> New ( 6 ) ; 
 seven := Node -> New ( 7 ) ; 
 eight := Node -> New ( 8 ) ; 
 nine := Node -> New ( 9 ) ; 

 one -> SetLeft ( two ) ; one -> SetRight ( three ) ; 
 two -> SetLeft ( four ) ; two -> SetRight ( five ) ; 
 three -> SetLeft ( six ) ; four -> SetLeft ( seven ) ; 
 six -> SetLeft ( eight ) ; six -> SetRight ( nine ) ; 

 "Preorder: " -> Print ( ) ; Preorder ( one ) ; 
 " \n Inorder: " -> Print ( ) ; Inorder ( one ) ; 
 " \n Postorder: " -> Print ( ) ; Postorder ( one ) ; 
 " \n Levelorder: " -> Print ( ) ; Levelorder ( one ) ; 
 " \n " -> Print ( ) ; 
  } 

 function : Preorder ( node : Node ) ~ Nil { 
 if ( node <> Nil ) { 
 System.IO.Console -> Print ( node -> GetData ( ) ) -> Print ( ", " ) ; 
 Preorder ( node -> GetLeft ( ) ) ; 
 Preorder ( node -> GetRight ( ) ) ; 
 } ; 
  } 

 function : Inorder ( node : Node ) ~ Nil { 
 if ( node <> Nil ) { 
 Inorder ( node -> GetLeft ( ) ) ; 
 System.IO.Console -> Print ( node -> GetData ( ) ) -> Print ( ", " ) ; 
 Inorder ( node -> GetRight ( ) ) ; 
 } ; 
  } 

 function : Postorder ( node : Node ) ~ Nil { 
 if ( node <> Nil ) { 
 Postorder ( node -> GetLeft ( ) ) ; 
 Postorder ( node -> GetRight ( ) ) ; 
 System.IO.Console -> Print ( node -> GetData ( ) ) -> Print ( ", " ) ; 
 } ; 
  } 

 function : Levelorder ( node : Node ) ~ Nil { 
 nodequeue := Collection.Queue -> New ( ) ; 
 if ( node <> Nil ) { 
 nodequeue -> Add ( node ) ; 
 } ; 

 while ( nodequeue -> IsEmpty ( ) = false ) { 
 next := nodequeue -> Remove ( ) -> As ( Node ) ; 
 System.IO.Console -> Print ( next -> GetData ( ) ) -> Print ( ", " ) ; 
 if ( next -> GetLeft ( ) <> Nil ) { 
 nodequeue -> Add ( next -> GetLeft ( ) ) ; 
 } ; 

 if ( next -> GetRight ( ) <> Nil ) { 
 nodequeue -> Add ( next -> GetRight ( ) ) ; 
 } ; 
 } ; 
  } 
  } 

 class Node from BasicCompare { 
 @left : Node ; 
 @right : Node ; 
 @data : Int ; 

 New ( data : Int ) { 
 Parent ( ) ; 
 @data := data ; 
  } 

 method : public : GetData ( ) ~ Int { 
 return @data ; 
  } 

 method : public : SetLeft ( left : Node ) ~ Nil { 
 @left := left ; 
  } 

 method : public : GetLeft ( ) ~ Node { 
 return @left ; 
  } 

 method : public : SetRight ( right : Node ) ~ Nil { 
 @right := right ; 
  } 

 method : public : GetRight ( ) ~ Node { 
 return @right ; 
  } 

 method : public : Compare ( rhs : Compare ) ~ Int { 
 right : Node := rhs -> As ( Node ) ; 
 if ( @data = right -> GetData ( ) ) { 
 return 0 ; 
  } 
 else if ( @data < right -> GetData ( ) ) { 
 return - 1 ; 
 } ; 

 return 1 ; 
  } 
  }

Output:

 Preorder: 1, 2, 4, 7, 5, 3, 6, 8, 9, 
Inorder: 7, 4, 2, 5, 1, 8, 6, 9, 3, 
Postorder: 7, 4, 5, 2, 8, 9, 6, 3, 1, 
Levelorder: 1, 2, 3, 4, 5, 6, 7, 8, 9,

[edit] OCaml

 type ' a tree = Empty 
  | Node of ' a * ' a tree * ' a tree 

 let rec preorder f = function 
 Empty -> ( ) 
  | Node ( v,l,r ) -> fv ; 
 preorder fl ; 
 preorder fr 

 let rec inorder f = function 
 Empty -> ( ) 
  | Node ( v,l,r ) -> inorder fl ; 
 fv ; 
 inorder fr 

 let rec postorder f = function 
 Empty -> ( ) 
  | Node ( v,l,r ) -> postorder fl ; 
 postorder fr ; 
 fv 

 let levelorder fx = 
 let queue = Queue . create ( ) in 
 Queue . add x queue ; 
 while not ( Queue . is_empty queue ) do 
 match Queue . take queue with 
 Empty -> ( ) 
  | Node ( v,l,r ) -> fv ; 
 Queue . add l queue ; 
 Queue . add r queue 
 done 

 let tree = 
 Node ( 1 , 
 Node ( 2 , 
 Node ( 4 , 
 Node ( 7 , Empty, Empty ) , 
 Empty ) , 
 Node ( 5 , Empty, Empty ) ) , 
 Node ( 3 , 
 Node ( 6 , 
 Node ( 8 , Empty, Empty ) , 
 Node ( 9 , Empty, Empty ) ) , 
 Empty ) ) 

 let ( ) = 
 preorder ( Printf . printf "%d " ) tree ; print_newline ( ) ; 
 inorder ( Printf . printf "%d " ) tree ; print_newline ( ) ; 
 postorder ( Printf . printf "%d " ) tree ; print_newline ( ) ; 
 levelorder ( Printf . printf "%d " ) tree ; print_newline ( )

Output:

 1 2 4 7 5 3 6 8 9 
7 4 2 5 1 8 6 9 3 
2 4 7 5 3 6 8 9 1 
1 2 3 4 5 6 7 8 9

[edit] ooRexx

 one = . Node~new ( 1 ) ; 
 two = . Node~new ( 2 ) ; 
 three = . Node~new ( 3 ) ; 
 four = . Node~new ( 4 ) ; 
 five = . Node~new ( 5 ) ; 
 six = . Node~new ( 6 ) ; 
 seven = . Node~new ( 7 ) ; 
 eight = . Node~new ( 8 ) ; 
 nine = . Node~new ( 9 ) ; 

 one~ left = two 
 one~ right = three 
 two~ left = four 
 two~ right = five 
 three~ left = six 
 four~ left = seven 
 six~ left = eight 
 six~ right = nine 

 out = . array~new 
  . treetraverser~preorder ( one, out ) ; 
 say "Preorder: " out~toString ( "l" , ", " ) 
 out~empty 
  . treetraverser~inorder ( one, out ) ; 
 say "Inorder: " out~toString ( "l" , ", " ) 
 out~empty 
  . treetraverser~postorder ( one, out ) ; 
 say "Postorder: " out~toString ( "l" , ", " ) 
 out~empty 
  . treetraverser~levelorder ( one, out ) ; 
 say "Levelorder:" out~toString ( "l" , ", " ) 


 ::class node 
 ::method init 
 expose left right data 
 use strict arg data 
 left = . nil 
 right = . nil 

 :: attribute left 
 :: attribute right 
 :: attribute data 

 ::class treeTraverser 
 ::method preorder class 
 use arg node, out 
 if node \ == . nil then do 
 out~append ( node~data ) 
 self~preorder ( node~ left , out ) 
 self~preorder ( node~ right , out ) 
  end 

 ::method inorder class 
 use arg node, out 
 if node \ == . nil then do 
 self~inorder ( node~ left , out ) 
 out~append ( node~data ) 
 self~inorder ( node~ right , out ) 
  end 

 ::method postorder class 
 use arg node, out 
 if node \ == . nil then do 
 self~postorder ( node~ left , out ) 
 self~postorder ( node~ right , out ) 
 out~append ( node~data ) 
  end 

 ::method levelorder class 
 use arg node, out 

 if node == . nil then return 
 nodequeue = . queue ~new 
 nodequeue~ queue ( node ) 
 loop while \ nodequeue~isEmpty 
 next = nodequeue~ pull 
 out~append ( next~data ) 
 if next~ left \ = . nil then 
 nodequeue~ queue ( next~ left ) 
 if next~ right \ = . nil then 
 nodequeue~ queue ( next~ right ) 
  end

Output:

 Preorder: 1, 2, 4, 7, 5, 3, 6, 8, 9
Inorder: 7, 4, 2, 5, 1, 8, 6, 9, 3
Postorder: 7, 4, 5, 2, 8, 9, 6, 3, 1
Levelorder: 1, 2, 3, 4, 5, 6, 7, 8, 9

[edit] Oz

 declare 
 Tree = n ( 1 
 n ( 2 
 n ( 4 n ( 7 ee ) e ) 
 n ( 5 ee ) ) 
 n ( 3 
 n ( 6 n ( 8 ee ) n ( 9 ee ) ) 
 e ) ) 

 fun { Concat Xs } 
 { FoldR Xs Append nil } 
  end 

 fun { Preorder T } 
 case T of e then nil 
 [ ] n ( VLR ) then 
 { Concat [ [ V ] 
 { Preorder L } 
 { Preorder R } ] } 
  end 
  end 

 fun { Inorder T } 
 case T of e then nil 
 [ ] n ( VLR ) then 
 { Concat [ { Inorder L } 
 [ V ] 
 { Inorder R } ] } 
  end 
  end 

 fun { Postorder T } 
 case T of e then nil 
 [ ] n ( VLR ) then 
 { Concat [ { Postorder L } 
 { Postorder R } 
 [ V ] ] } 
  end 
  end 

  local 
 fun { Collect Queue } 
 case Queue of nil then nil 
 [ ] e | Xr then { Collect Xr } 
 [ ] n ( VLR ) | Xr then 
 V | { Collect { Append Xr [ LR ] } } 
  end 
  end 
 in 
 fun { Levelorder T } 
 { Collect [ T ] } 
  end 
  end 
 in 
 { Show { Preorder Tree } } 
 { Show { Inorder Tree } } 
 { Show { Postorder Tree } } 
 { Show { Levelorder Tree } }

[edit] Perl

Tree nodes are represented by 3-element arrays: [0] - the value; [1] - left child; [2] - right child.

 sub preorder 
  { 
 my $t = shift or return ( ) ; 
 return ( $t -> [ 0 ] , preorder ( $t -> [ 1 ] ) , preorder ( $t -> [ 2 ] ) ) ; 
  } 

 sub inorder 
  { 
 my $t = shift or return ( ) ; 
 return ( inorder ( $t -> [ 1 ] ) , $t -> [ 0 ] , inorder ( $t -> [ 2 ] ) ) ; 
  } 

 sub postorder 
  { 
 my $t = shift or return ( ) ; 
 return ( postorder ( $t -> [ 1 ] ) , postorder ( $t -> [ 2 ] ) , $t -> [ 0 ] ) ; 
  } 

 sub depth 
  { 
 my @ret ; 
 my @a = ( $_ [ 0 ] ) ; 
 while ( @a ) { 
 my $v = shift @a or next ; 
 push @ret , $v -> [ 0 ] ; 
 push @a , @ { $v } [ 1 , 2 ] ; 
  } 
 return @ret ; 
  } 

 my $x = [ 1 , [ 2 , [ 4 , [ 7 ] ] , [ 5 ] ] , [ 3 , [ 6 , [ 8 ] , [ 9 ] ] ] ] ; 

 print "pre: @{[preorder($x)]} \n " ; 
 print "in: @{[inorder($x)]} \n " ; 
 print "post: @{[postorder($x)]} \n " ; 
 print "depth: @{[depth($x)]} \n " ;

Output:

 pre: 1 2 4 7 5 3 6 8 9
in: 7 4 2 5 1 8 6 9 3
post: 7 4 5 2 8 9 6 3 1
depth: 1 2 3 4 5 6 7 8 9

[edit] Perl 6

 class TreeNode { 
 has TreeNode $ . parent ; 
 has TreeNode $ . left ; 
 has TreeNode $ . right ; 
 has $ . value ; 

 method pre - order { 
 gather { 
 take $ . value ; 
 take $ . left . pre - order if $ . left ; 
 take $ . right . pre - order if $ . right 
  } 
  } 

 method in - order { 
 gather { 
 take $ . left . in - order if $ . left ; 
 take $ . value ; 
 take $ . right . in - order if $ . right ; 
  } 
  } 

 method post - order { 
 gather { 
 take $ . left . post - order if $ . left ; 
 take $ . right . post - order if $ . right ; 
 take $ . value ; 
  } 
  } 

 method level - order { 
 my TreeNode @queue = ( self ) ; 
 gather while @queue . elems { 
 my $n = @queue . shift ; 
 take $n . value ; 
 @queue . push ( $n . left ) if $n . left ; 
 @queue . push ( $n . right ) if $n . right ; 
  } 
  } 
  } 

 my TreeNode $root .= new ( value => 1 , 
 left => TreeNode . new ( value => 2 , 
 left => TreeNode . new ( value => 4 , left => TreeNode . new ( value => 7 ) ) , 
 right => TreeNode . new ( value => 5 ) 
 ) , 
 right => TreeNode . new ( value => 3 , 
 left => TreeNode . new ( value => 6 , 
 left => TreeNode . new ( value => 8 ) , 
 right => TreeNode . new ( value => 9 ) 
  ) 
  ) 
  ) ; 

 say "preorder: " , $root . pre - order . join ( " " ) ; 
 say "inorder: " , $root . in - order . join ( " " ) ; 
 say "postorder: " , $root . post - order . join ( " " ) ; 
 say "levelorder:" , $root . level - order . join ( " " ) ;

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
levelorder:1 2 3 4 5 6 7 8 9

[edit] PicoLisp

 (de preorder (Node Fun) 
 (when Node 
 (Fun (car Node)) 
 (preorder (cadr Node) Fun) 
 (preorder (caddr Node) Fun) ) ) 

 (de inorder (Node Fun) 
 (when Node 
 (inorder (cadr Node) Fun) 
 (Fun (car Node)) 
 (inorder (caddr Node) Fun) ) ) 

 (de postorder (Node Fun) 
 (when Node 
 (postorder (cadr Node) Fun) 
 (postorder (caddr Node) Fun) 
 (Fun (car Node)) ) ) 

 (de level-order (Node Fun) 
 (for (Q (circ Node) Q) 
 (let N (fifo 'Q) 
 (Fun (car N)) 
 (and (cadr N) (fifo 'Q @)) 
 (and (caddr N) (fifo 'Q @)) ) ) ) 

 (setq *Tree 
 (1 
 (2 (4 (7)) (5)) 
 (3 (6 (8) (9))) ) ) 

 (for Order '(preorder inorder postorder level-order) 
 (prin (align -13 (pack Order ":"))) 
 (Order *Tree printsp) 
 (prinl) )

Output:

 preorder: 1 2 4 7 5 3 6 8 9 
inorder: 7 4 2 5 1 8 6 9 3 
postorder: 7 4 5 2 8 9 6 3 1 
level-order: 1 2 3 4 5 6 7 8 9

[edit] Prolog

Works with SWI-Prolog.

 tree :- 
 Tree = [ 1 , 
 [ 2 , 
 [ 4 , 
 [ 7 , nil , nil ] , 
 nil ] , 
 [ 5 , nil , nil ] ] , 
 [ 3 , 
 [ 6 , 
 [ 8 , nil , nil ] , 
 [ 9 , nil , nil ] ] , 
 nil ] ] , 

 write ( 'preorder  : ' ) , preorder ( Tree ) , nl , 
 write ( 'inorder  : ' ) , inorder ( Tree ) , nl , 
 write ( 'postorder  : ' ) , postorder ( Tree ) , nl , 
 write ( 'level-order : ' ) , level_order ( [ Tree ] ) . 

 preorder ( nil ) . 
 preorder ( [ Node , FG , FD ] ) :- 
 format ( '~w ' , [ Node ] ) , 
 preorder ( FG ) , 
 preorder ( FD ) . 


 inorder ( nil ) . 
 inorder ( [ Node , FG , FD ] ) :- 
 inorder ( FG ) , 
 format ( '~w ' , [ Node ] ) , 
 inorder ( FD ) . 

 postorder ( nil ) . 
 postorder ( [ Node , FG , FD ] ) :- 
 postorder ( FG ) , 
 postorder ( FD ) , 
 format ( '~w ' , [ Node ] ) . 


 level_order ( [ ] ) . 

 level_order ( A ) :- 
 level_order_ ( A , U - U , S ) , 
 level_order ( S ) . 

 level_order_ ( [ ] , S - [ ] , S ) . 

 level_order_ ( [ [ Node , FG , FD ] | T ] , CS , FS ) :- 
 format ( '~w ' , [ Node ] ) , 
 append_dl ( CS , [ FG , FD | U ] - U , CS1 ) , 
 level_order_ ( T , CS1 , FS ) . 

 level_order_ ( [ nil | T ] , CS , FS ) :- 
 level_order_ ( T , CS , FS ) . 


 append_dl ( X - Y , Y - Z , X - Z ) .

Output :

 ?- tree.
preorder  : 1 2 4 7 5 3 6 8 9 
inorder  : 7 4 2 5 1 8 6 9 3 
postorder  : 7 4 5 2 8 9 6 3 1 
level-order : 1 2 3 4 5 6 7 8 9 
true .

[edit] PureBasic

Works with : PureBasic version 4.5+
 Structure node 
 value.i 
 * left .node 
 * right .node 
 EndStructure 

 Structure queue 
 List qi ( ) 
 EndStructure 

 DataSection 
 tree: 
 Data .s "1(2(4(7),5),3(6(8,9)))" 
 EndDataSection 

 ;Convenient routine to interpret string data to construct a tree of integers. 
 Procedure createTree ( * n.node, * tPtr.Character ) 
 Protected num.s, * l.node, * ntPtr.Character 

 Repeat 
 Select * tPtr \ c 
 Case ' 0 ' To ' 9 ' 
 num + Chr ( * tPtr \ c ) 
 Case ' ( ' 
 * n \ value = Val ( num ) : num = "" 
 * ntPtr = * tPtr + 1 
 If * ntPtr \ c = ',' 
 ProcedureReturn * tPtr 
 Else 
 * l = AllocateMemory ( SizeOf ( node ) ) 
 * n \ left = * l: * tPtr = createTree ( * l, * ntPtr ) 
 EndIf 
 Case ' ) ', ',', #Null 
 If num: * n \ value = Val ( num ) : EndIf 
 ProcedureReturn * tPtr 
 EndSelect 

 If * tPtr \ c = ',' 
 * l = AllocateMemory ( SizeOf ( node ) ) : 
 * n \ right = * l: * tPtr = createTree ( * l, * tPtr + 1 ) 
 EndIf 
 * tPtr + 1 
 ForEver 
 EndProcedure 

 Procedure enqueue ( List qi ( ) , element ) 
 LastElement ( q ( ) ) 
 AddElement ( q ( ) ) 
 q ( ) = element 
 EndProcedure 

 Procedure dequeue ( List qi ( ) ) 
 Protected element 
 If FirstElement ( q ( ) ) 
 element = q ( ) 
 DeleteElement ( q ( ) ) 
 EndIf 
 ProcedureReturn element 
 EndProcedure 

 Procedure onVisit ( * n.node ) 
 Print ( Str ( * n \ value ) + " " ) 
 EndProcedure 

 Procedure preorder ( * n.node ) ;recursive 
 onVisit ( * n ) 
 If * n \ left 
 preorder ( * n \ left ) 
 EndIf 
 If * n \ right 
 preorder ( * n \ right ) 
 EndIf 
 EndProcedure 

 Procedure inorder ( * n.node ) ;recursive 
 If * n \ left 
 inorder ( * n \ left ) 
 EndIf 
 onVisit ( * n ) 
 If * n \ right 
 inorder ( * n \ right ) 
 EndIf 
 EndProcedure 

 Procedure postorder ( * n.node ) ;recursive 
 If * n \ left 
 postorder ( * n \ left ) 
 EndIf 
 If * n \ right 
 postorder ( * n \ right ) 
 EndIf 
 onVisit ( * n ) 
 EndProcedure 

 Procedure levelorder ( * n.node ) 
 Dim q.queue ( 1 ) 
 Protected readQueue = 1 , writeQueue, * currNode.node 

 enqueue ( q ( writeQueue ) \ q ( ) , * n ) ;start queue off with root 
 Repeat 
 readQueue ! 1 : writeQueue !  one 
 While ListSize ( q ( readQueue ) \ q ( ) ) 
 * currNode = dequeue ( q ( readQueue ) \ q ( ) ) 
 If * currNode \ left 
 enqueue ( q ( writeQueue ) \ q ( ) , * currNode \ left ) 
 EndIf 
 If * currNode \ right 
 enqueue ( q ( writeQueue ) \ q ( ) , * currNode \ right ) 
 EndIf 
 onVisit ( * currNode ) 
 Wend 
 Until ListSize ( q ( writeQueue ) \ q ( ) ) = 0 
 EndProcedure 

 If OpenConsole ( ) 
 Define root.node 
 createTree ( root,?tree ) 

 Print ( "preorder: " ) 
 preorder ( root ) 
 PrintN ( "" ) 
 Print ( "inorder: " ) 
 inorder ( root ) 
 PrintN ( "" ) 
 Print ( "postorder: " ) 
 postorder ( root ) 
 PrintN ( "" ) 
 Print ( "levelorder: " ) 
 levelorder ( root ) 
 PrintN ( "" ) 

 Print ( #CRLF$ + #CRLF$ + "Press ENTER to exit" ) 
 Input ( ) 
 CloseConsole ( ) 
 EndIf

Sample output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
levelorder: 1 2 3 4 5 6 7 8 9

[edit] Python

 from collections import namedtuple 
 from sys import stdout 

 Node = namedtuple ( 'Node' , 'data, left, right' ) 
 tree = Node ( 1 , 
 Node ( 2 , 
 Node ( 4 , 
 Node ( 7 , None , None ) , 
 None ) , 
 Node ( 5 , None , None ) ) , 
 Node ( 3 , 
 Node ( 6 , 
 Node ( 8 , None , None ) , 
 Node ( 9 , None , None ) ) , 
 None ) ) 

 def printwithspace ( i ) : 
 stdout. write ( "%i " % i ) 

 def preorder ( node , visitor = printwithspace ) : 
 if node is not None : 
 visitor ( node. data ) 
 preorder ( node. left , visitor ) 
 preorder ( node. right , visitor ) 

 def inorder ( node , visitor = printwithspace ) : 
 if node is not None : 
 inorder ( node. left , visitor ) 
 visitor ( node. data ) 
 inorder ( node. right , visitor ) 

 def postorder ( node , visitor = printwithspace ) : 
 if node is not None : 
 postorder ( node. left , visitor ) 
 postorder ( node. right , visitor ) 
 visitor ( node. data ) 

 def levelorder ( node , more = None , visitor = printwithspace ) : 
 if node is not None : 
 if more is None : 
 more = [ ] 
 more + = [ node. left , node. right ] 
 visitor ( node. data ) 
 if more: 
 levelorder ( more [ 0 ] , more [ 1 : ] , visitor ) 

 stdout. write ( ' preorder: ' ) 
 preorder ( tree ) 
 stdout. write ( ' \n inorder: ' ) 
 inorder ( tree ) 
 stdout. write ( ' \n postorder: ' ) 
 postorder ( tree ) 
 stdout. write ( ' \n levelorder: ' ) 
 levelorder ( tree ) 
 stdout. write ( ' \n ' )

Sample output:

 preorder: 1 2 4 7 5 3 6 8 9 
   inorder: 7 4 2 5 1 8 6 9 3 
 postorder: 7 4 5 2 8 9 6 3 1 
levelorder: 1 2 3 4 5 6 7 8 9

[edit] Qi

 (set *tree* [1 [2 [4 [7]] 
 [5]] 
 [3 [6 [8] 
 [9]]]]) 

 (define inorder 
 [] -> [] 
 [V] -> [V] 
 [VL] -> (append (inorder L) 
 [V]) 
 [VLR] -> (append (inorder L) 
 [V] 
 (inorder R))) 

 (define postorder 
 [] -> [] 
 [V] -> [V] 
 [VL] -> (append (postorder L) 
 [V]) 
 [VLR] -> (append (postorder L) 
 (postorder R) 
 [V])) 

 (define preorder 
 [] -> [] 
 [V] -> [V] 
 [VL] -> (append [V] 
 (preorder L)) 
 [VLR] -> (append [V] 
 (preorder L) 
 (preorder R))) 

 (define levelorder-0 
 [] -> [] 
 [[] | Q] -> (levelorder-0 Q) 
 [[V | LR] | Q] -> [V | (levelorder-0 (append Q LR))]) 

 (define levelorder 
 Node -> (levelorder-0 [Node])) 

 (preorder (value *tree*)) 
 (postorder (value *tree*)) 
 (inorder (value *tree*)) 
 (levelorder (value *tree*))

Output:

 [1 2 4 7 5 3 6 8 9]
[7 4 2 5 1 8 6 9 3]
[7 4 5 2 8 9 6 3 1]
[1 2 3 4 5 6 7 8 9]

[edit] Racket

 #lang racket 

 (define the-tree ; Node: (list   ) 
 '(1 (2 (4 (7 #f #f) #f) (5 #f #f)) (3 (6 (8 #f #f) (9 #f #f)) #f))) 

 (define (preorder tree visit) 
 (let loop ([t tree]) 
 (when t (visit (car t)) (loop (cadr t)) (loop (caddr t))))) 
 (define (inorder tree visit) 
 (let loop ([t tree]) 
 (when t (loop (cadr t)) (visit (car t)) (loop (caddr t))))) 
 (define (postorder tree visit) 
 (let loop ([t tree]) 
 (when t (loop (cadr t)) (loop (caddr t)) (visit (car t))))) 
 (define (levelorder tree visit) 
 (let loop ([trees (list tree)]) 
 (unless (null? trees) 
 ((compose1 loop (curry filter values) append*) 
 (for/list ([t trees] #:when t) (visit (car t)) (cdr t)))))) 

 (define (run order) 
 (printf "~a:" (object-name order)) 
 (order the-tree (λ(x) (printf " ~s" x))) 
 (newline)) 
 (for-each run (list preorder inorder postorder levelorder))

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
levelorder: 1 2 3 4 5 6 7 8 9

[edit] REXX

 /* REXX *************************************************************** 
 * Tree traversal 
 = 1 
 = / \ 
 = / \ 
 = / \ 
 = 2 3 
 = / \ / 
 = 4 5 6 
 = / / \ 
 = 7 8 9 
  = 
 = The correct output should look like this: 
 = preorder: 1 2 4 7 5 3 6 8 9 
 = level-order: 1 2 3 4 5 6 7 8 9 
 = postorder: 7 4 5 2 8 9 6 3 1 
 = inorder: 7 4 2 5 1 8 6 9 3 

 * 17.06.2012 Walter Pachl not thoroughly tested 
 **********************************************************************/ 
 debug= 0 
 wl_soll= 1 2 4 7 5 3 6 8 9 
 il_soll= 7 4 2 5 1 8 6 9 3 
 pl_soll= 7 4 5 2 8 9 6 3 1 
 ll_soll= 1 2 3 4 5 6 7 8 9 

 Call mktree 
 wl . = '' ; wl= '' /* preorder */ 
 ll . = '' ; ll= '' /* level-order */ 
 il= '' /* inorder */ 
 pl= '' /* postorder */ 

 /********************************************************************** 
 * First walk the tree and construct preorder and level-order lists 
 **********************************************************************/ 
 done . = 0 
 lvl= 1 
 z=root 
 Call note z 
 Do Until z= 0 
 z=go_next ( z ) 
 Call note z 
 End 
 Call show 'preorder: ' ,wl,wl_soll 
 Do lvl= 1 To 4 
 ll=ll ll . lvl 
 End 
 Call show 'level-order:' ,ll,ll_soll 

 /********************************************************************** 
 * Next construct postorder list 
 **********************************************************************/ 
 done . = 0 
 ridone . = 0 
 z=lbot ( root ) 
 Call notep z 
 Do Until z= 0 
 br=brother ( z ) 
 If br > 0 & , 
 done . br= 0 Then Do 
 ridone . br= 1 
 z=lbot ( br ) 
 Call notep z 
 End 
 Else 
 z=father ( z ) 
 Call notep z 
 End 
 Call show 'postorder: ' ,pl,pl_soll 

 /********************************************************************** 
 * Finally construct inorder list 
 **********************************************************************/ 
 done . = 0 
 ridone . = 0 
 z=lbot ( root ) 
 Call notei z 
 Do Until z= 0 
 z=father ( z ) 
 Call notei z 
 ri=node . z . 0rite 
 If ridone . z= 0 Then Do 
 ridone . z= 1 
 If ri > 0 Then Do 
 z=lbot ( ri ) 
 Call notei z 
 End 
 End 
 End 

 /********************************************************************** 
 * And now show the results and check them for correctness 
 **********************************************************************/ 
 Call show 'inorder: ' ,il,il_soll 

 Exit 

 show: Parse Arg Which,have,soll 
 /********************************************************************** 
 * Show our result and show it it's correct 
 **********************************************************************/ 
 have= space ( have ) 
 If have=soll Then 
 tag= '' 
 Else 
 tag= '*wrong*' 
 Say which have tag 
 If tag <> '' Then 
 Say '------------>' soll 'is the expected result' 
 Return 

 brother: Procedure Expose node . 
 /********************************************************************** 
 * Return the right node of this node's father or 0 
 **********************************************************************/ 
 Parse arg no 
 nof=node . no . 0father 
 brot1=node . nof . 0rite 
 Return brot1 

 notei: Procedure Expose debug il done . 
 /********************************************************************** 
 * append the given node to il 
 **********************************************************************/ 
 Parse Arg nd 
 If nd <> 0 & , 
 done . nd= 0 Then 
 il=il nd 
 If debug Then 
 Say 'notei' nd 
 done . nd= 1 
 Return 

 notep: Procedure Expose debug pl done . 
 /********************************************************************** 
 * append the given node to pl 
 **********************************************************************/ 
 Parse Arg nd 
 If nd <> 0 & , 
 done . nd= 0 Then Do 
 pl=pl nd 
 If debug Then 
 Say 'notep' nd 
 End 
 done . nd= 1 
 Return 

 father: Procedure Expose node . 
 /********************************************************************** 
 * Return the father of the argument 
 * or 0 if the root is given as argument 
 **********************************************************************/ 
 Parse Arg nd 
 Return node . nd . 0father 

 lbot: Procedure Expose node . 
 /********************************************************************** 
 * From node z: Walk down on the left side until you reach the bottom 
 * and return the bottom node 
 * If z has no left son (at the bottom of the tree) returm itself 
 **********************************************************************/ 
 Parse Arg z 
 Do i= 1 To 100 
 If node . z . 0left <> 0 Then 
 z=node . z . 0left 
 Else 
 Leave 
 End 
 Return z 

 note: 
 /********************************************************************** 
 * add the node to the preorder list unless it's already there 
 * add the node to the level list 
 **********************************************************************/ 
 If z <> 0 & , /* it's a node */ 
 done . z= 0 Then Do /* not yet done */ 
 wl=wl z /* add it to the preorder list*/ 
 ll . lvl=ll . lvl z /* add it to the level list */ 
 done . z= 1 /* remember it's done */ 
 End 
 Return 

 go_next: Procedure Expose node . lvl 
 /********************************************************************** 
 * find the next node to visit in the treewalk 
 **********************************************************************/ 
 next= 0 
 Parse arg z 
 If node . z . 0left <> 0 Then Do /* there is a left son */ 
 If node . z . 0left . done= 0 Then Do /* we have not visited it */ 
 next=node . z . 0left /* so we go there */ 
 node . z . 0left . done= 1 /* note we were here */ 
 lvl=lvl+ 1 /* increase the level */ 
 End 
 End 
 If next= 0 Then Do /* not moved yet */ 
 If node . z . 0rite <> 0 Then Do /* there is a right son */ 
 If node . z . 0rite . done= 0 Then Do /* we have not visited it */ 
 next=node . z . 0rite /* so we go there */ 
 node . z . 0rite . done= 1 /* note we were here */ 
 lvl=lvl+ 1 /* increase the level */ 
 End 
 End 
 End 
 If next= 0 Then Do /* not moved yet */ 
 next=node . z . 0father /* go to the father */ 
 lvl=lvl- 1 /* decrease the level */ 
 End 
 Return next /* that's the next node */ 
 /* or zero if we are done */ 

 mknode: Procedure Expose node . 
 /********************************************************************** 
 * create a new node 
 **********************************************************************/ 
 Parse Arg name 
 z=node . 0+ 1 
 node . z . 0name= name 
 node . z . 0father= 0 
 node . z . 0left = 0 
 node . z . 0rite = 0 
 node . 0=z 
 Return z /* number of the node just created */ 

 attleft: Procedure Expose node . 
 /********************************************************************** 
 * make son the left son of father 
 **********************************************************************/ 
 Parse Arg son,father 
 node . son . 0father=father 
 z=node . father . 0left 
 If z <> 0 Then Do 
 node . z . 0father=son 
 node . son . 0left=z 
 End 
 node . father . 0left=son 
 Return 

 attrite: Procedure Expose node . 
 /********************************************************************** 
 * make son the right son of father 
 **********************************************************************/ 
 Parse Arg son,father 
 node . son . 0father=father 
 z=node . father . 0rite 
 If z <> 0 Then Do 
 node . z . 0father=son 
 node . son . 0rite=z 
 End 
 node . father . 0rite=son 
 le=node . father . 0left 
 If le > 0 Then 
 node . le . 0brother=node . father . 0rite 
 Return 

 mktree: Procedure Expose node . root 
 /********************************************************************** 
 * build the tree according to the task 
 **********************************************************************/ 
 node . = 0 
 a=mknode ( 'A' ) ; root=a 
 b=mknode ( 'B' ) ; Call attleft b,a 
 c=mknode ( 'C' ) ; Call attrite c,a 
 d=mknode ( 'D' ) ; Call attleft d,b 
 e=mknode ( 'E' ) ; Call attrite e,b 
 f=mknode ( 'F' ) ; Call attleft f,c 
 g=mknode ( 'G' ) ; Call attleft g,d 
 h=mknode ( 'H' ) ; Call attleft h,f 
 i=mknode ( 'I' ) ; Call attrite i,f 
 Call show_tree 1 
 Return 

 show_tree: Procedure Expose node . 
 /********************************************************************** 
 * Show the tree 
 * f 
 * l1 1 r1 
 * lrlr 
 * lrlrlrlr 
 * 12345678901234567890 
 **********************************************************************/ 
 Parse Arg f 
 l . = '' 
 l . 1= overlay ( f ,l . 1, 9 ) 

 l1=node .  f . 0left  ;l . 2= overlay ( l1 ,l . 2, 5 ) 
 /*b1=node.f.0brother  ;l.2=overlay(b1 ,l.2, 9) */ 
 r1=node .  f . 0rite  ;l . 2= overlay ( r1 ,l . 2, 13 ) 

 l1g=node . l1 . 0left  ;l . 3= overlay ( l1g ,l . 3, 3 ) 
 /*b1g=node.l1.0brother  ;l.3=overlay(b1g ,l.3, 5) */ 
 r1g=node . l1 . 0rite  ;l . 3= overlay ( r1g ,l . 3, 7 ) 

 l2g=node . r1 . 0left  ;l . 3= overlay ( l2g ,l . 3, 11 ) 
 /*b2g=node.r1.0brother  ;l.3=overlay(b2g ,l.3,13) */ 
 r2g=node . r1 . 0rite  ;l . 3= overlay ( r2g ,l . 3, 15 ) 

 l1ls=node . l1g . 0left  ;l . 4= overlay ( l1ls,l . 4, 2 ) 
 /*b1ls=node.l1g.0brother ;l.4=overlay(b1ls,l.4, 3) */ 
 r1ls=node . l1g . 0rite  ;l . 4= overlay ( r1ls,l . 4, 4 ) 

 l1rs=node . r1g . 0left  ;l . 4= overlay ( l1rs,l . 4, 6 ) 
 /*b1rs=node.r1g.0brother ;l.4=overlay(b1rs,l.4, 7) */ 
 r1rs=node . r1g . 0rite  ;l . 4= overlay ( r1rs,l . 4, 8 ) 

 l2ls=node . l2g . 0left  ;l . 4= overlay ( l2ls,l . 4, 10 ) 
 /*b2ls=node.l2g.0brother ;l.4=overlay(b2ls,l.4,11) */ 
 r2ls=node . l2g . 0rite  ;l . 4= overlay ( r2ls,l . 4, 12 ) 

 l2rs=node . r2g . 0left  ;l . 4= overlay ( l2rs,l . 4, 14 ) 
 /*b2rs=node.r2g.0brother ;l.4=overlay(b2rs,l.4,15) */ 
 r2rs=node . r2g . 0rite  ;l . 4= overlay ( r2rs,l . 4, 16 ) 
 Do i= 1 To 4 
 Say translate ( l . i, ' ' , '0' ) 
 Say '' 
 End 
 Return

Output:

  one

     2 3

  4 5 6

 7 8 9

preorder: 1 2 4 7 5 3 6 8 9
level-order: 1 2 3 4 5 6 7 8 9
postorder: 7 4 5 2 8 9 6 3 1
inorder: 7 4 2 5 1 8 6 9 3

[edit] Ruby

 BinaryTreeNode = Struct . new ( :value , :left , :right ) do 
 def self . from_array ( nested_list ) 
 value, left, right = nested_list 
 if value 
 self . new ( value, self . from_array ( left ) , self . from_array ( right ) ) 
  end 
  end 

 def walk_nodes ( order, & block ) 
 order. each do | node | 
 case node 
 when :left then left && left. walk_nodes ( order, & block ) 
 when : self then yield self 
 when :right then right && right. walk_nodes ( order, & block ) 
  end 
  end 
  end 

 def each_preorder ( & b ) walk_nodes ( [ : self , :left , :right ] , & b ) end 
 def each_inorder ( & b ) walk_nodes ( [ :left , : self , :right ] , & b ) end 
 def each_postorder ( & b ) walk_nodes ( [ :left , :right , : self ] , & b ) end 

 def each_levelorder 
 queue = [ self ] 
 until queue. empty ? 
 node = queue. shift 
 yield node 
 queue << node. left if node. left 
 queue << node. right if node. right 
  end 
  end 
  end 

 root = BinaryTreeNode. from_array [ 1 , [ 2 , [ 4 , 7 ] , [ 5 ] ] , [ 3 , [ 6 , [ 8 ] , [ 9 ] ] ] ] 

 BinaryTreeNode. instance_methods . select { | m | m=~ / . + order / } . each do | mthd | 
 printf "%-11s " , mthd [ 5 .. - 1 ] + ':' 
 root. send ( mthd ) { | node | print "#{node.value} " } 
 puts 
  end

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
levelorder: 1 2 3 4 5 6 7 8 9

[edit] Scala

Works with : Scala version 2.11.x
 case class IntNode ( value : Int, left : Option [ IntNode ] = None, right : Option [ IntNode ] = None ) { 

 def preorder ( f : IntNode => Unit ) { 
 f ( this ) 
 left. map ( _ . preorder ( f ) ) // Same as: if(left.isDefined) left.get.preorder(f) 
 right. map ( _ . preorder ( f ) ) 
  } 

 def postorder ( f : IntNode => Unit ) { 
 left. map ( _ . postorder ( f ) ) 
 right. map ( _ . postorder ( f ) ) 
 f ( this ) 
  } 

 def inorder ( f : IntNode => Unit ) { 
 left. map ( _ . inorder ( f ) ) 
 f ( this ) 
 right. map ( _ . inorder ( f ) ) 
  } 

 def levelorder ( f : IntNode => Unit ) { 

 def loVisit ( ls : List [ IntNode ] ) : Unit = ls match { 
 case Nil => None 
 case node :: rest => f ( node ) ; loVisit ( rest ++ node. left ++ node. right ) 
  } 

 loVisit ( List ( this ) ) 
  } 
  } 

 object TreeTraversal extends App { 
 implicit def intNode2SomeIntNode ( n : IntNode ) = Some [ IntNode ] ( n ) 

 val tree = IntNode ( 1 , 
 IntNode ( 2 , 
 IntNode ( 4 , 
 IntNode ( 7 ) ) , 
 IntNode ( 5 ) ) , 
 IntNode ( 3 , 
 IntNode ( 6 , 
 IntNode ( 8 ) , 
 IntNode ( 9 ) ) ) ) 

 List ( 
 " preorder: " - > tree. preorder _ , // `_` denotes the function value of type `IntNode => Unit` (returning nothing) 
 " inorder: " - > tree. inorder _ , 
 " postorder: " - > tree. postorder _ , 
 "levelorder: " - > tree. levelorder _ ) foreach { 
 case ( name, func ) => 
 val s = new StringBuilder ( name ) 
 func ( n => s ++ = n. value . toString + " " ) 
 println ( s ) 
  } 
  }
Output: 
 preorder: 1 2 4 7 5 3 6 8 9 
   inorder: 7 4 2 5 1 8 6 9 3 
 postorder: 7 4 5 2 8 9 6 3 1 
levelorder: 1 2 3 4 5 6 7 8 9

[edit] Tcl

Works with : Tcl version 8.6
or
Library: TclOO
 oo:: class create tree { 
 # Basic tree data structure stuff... 
 variable val lr 
 constructor { value { left { } } { right { } } } { 
 set val $value 
 set l $left 
 set r $right 
  } 
 method value { } { return $val } 
 method left { } { return $l } 
 method right { } { return $r } 
 destructor { 
 if { $l ne "" } { $l destroy } 
 if { $r ne "" } { $r destroy } 
  } 

 # Traversal methods 
 method preorder { varName script { level 0 } } { 
 upvar [ incr level ] $varName var 
 set var $val 
 uplevel $level $script 
 if { $l ne "" } { $l preorder $varName $script $level } 
 if { $r ne "" } { $r preorder $varName $script $level } 
  } 
 method inorder { varName script { level 0 } } { 
 upvar [ incr level ] $varName var 
 if { $l ne "" } { $l inorder $varName $script $level } 
 set var $val 
 uplevel $level $script 
 if { $r ne "" } { $r inorder $varName $script $level } 
  } 
 method postorder { varName script { level 0 } } { 
 upvar [ incr level ] $varName var 
 if { $l ne "" } { $l postorder $varName $script $level } 
 if { $r ne "" } { $r postorder $varName $script $level } 
 set var $val 
 uplevel $level $script 
  } 
 method levelorder { varName script } { 
 upvar 1 $varName var 
 set nodes [ list [ self ] ] ; # A queue of nodes to process 
 while { [ llength $nodes ] > 0 } { 
 set nodes [ lassign $nodes n ] 
 set var [ $n value ] 
 uplevel 1 $script 
 if { [ $n left ] ne "" } { lappend nodes [ $n left ] } 
 if { [ $n right ] ne "" } { lappend nodes [ $n right ] } 
  } 
  } 
  }

Note that in Tcl it is conventional to handle performing something “for each element” by evaluating a script in the caller's scope for each node after setting a caller-nominated variable to the value for that iteration. Doing this transparently while recursing requires the use of a varying 'level' parameter to upvar and uplevel , but makes for compact and clear code.

Demo code to satisfy the official challenge instance:

 # Helpers to make construction and listing of a whole tree simpler 
 proc Tree nested { 
 lassign $nested vlr 
 if { $l ne "" } { set l [ Tree $l ] } 
 if { $r ne "" } { set r [ Tree $r ] } 
 tree new $v $l $r 
  } 
 proc Listify { tree order } { 
 set list { } 
 $tree $order v { 
 lappend list $v 
  } 
 return $list 
  } 

 # Make a tree, print it a few ways, and destroy the tree 
 set t [ Tree { 1 { 2 { 4 7 } 5 } { 3 { 6 8 9 } } } ] 
 puts "preorder: [Listify $t preorder]" 
 puts "inorder: [Listify $t inorder]" 
 puts "postorder: [Listify $t postorder]" 
 puts "level-order: [Listify $t levelorder]" 
 $t destroy

Output:

 preorder: 1 2 4 7 5 3 6 8 9
inorder: 7 4 2 5 1 8 6 9 3
postorder: 7 4 5 2 8 9 6 3 1
level-order: 1 2 3 4 5 6 7 8 9

[edit] UNIX Shell

Bash (also "sh" on most Unix systems) has arrays. We implement a node as an association between three arrays: left, right, and value.

 left = ( ) 
 right = ( ) 
 value = ( ) 

 # node node#, left#, right#, value 
  # 
 # if value is empty, use node# 

 node ( ) { 
 nx = ${1:-'Missing node index'} 
 leftx = ${2} 
 rightx = ${3} 
 val = ${4:-$1} 
 value [ $nx ] = " $val " 
 left [ $nx ] = " $leftx " 
 right [ $nx ] = " $rightx " 
  } 

 # define the tree 

 node 1 2 3 
 node 2 4 5 
 node 3 6 
 node 4 7 
 node 5 
 node 6 8 9 
 node 7 
 node 8 
 node 9 

 # walk NODE# ORDER 

 walk ( ) { 
 local nx = ${1-"Missing index"} 
 shift 
 for branch in "$@" ; do 
 case " $branch " in 
 left ) if [ [ " ${left[$nx]} " ] ] ; then walk ${left[$nx]} $ @ ; fi ;; 
 right ) if [ [ " ${right[$nx]} " ] ] ; then walk ${right[$nx]} $ @ ; fi ;; 
 self ) printf "%d " " ${value[$nx]} " ;; 
 esac 
 done 
  } 

 apush ( ) { 
 local var = "$1" 
 eval " $var =( \" \$ { $var [@]} \" \" $2 \" )" 
  } 

 showname ( ) { 
 printf "%-12s " "$1:" 
  } 

 showdata ( ) { 
 showname "$1" 
 shift 
 walk "$@" 
 echo '' 
  } 

 preorder ( ) { showdata $FUNCNAME $1 self left right ;  } 
 inorder ( ) { showdata $FUNCNAME $1 left self right ;  } 
 postorder ( ) { showdata $FUNCNAME $1 left right self ;  } 
 levelorder ( ) { 
 showname 'level-order' 
 queue = ( $1 ) 
 x = 0 
 while [ [ $x < ${#queue[*]} ] ] ; do 
 value = " ${queue[$x]} " 
 printf "%d " " $value " 
 for more in " ${left[$value]} " " ${right[$value]} " ; do 
 if [ [ -n " $more " ] ] ;  then 
 apush queue " $more " 
  fi 
 done 
  : $ ( ( x++ ) ) 
 done 
 echo '' 
  } 

 preorder 1 
 inorder 1 
 postorder 1 
 levelorder 1

The output:

 preorder: 1 2 4 7 5 3 6 8 9 
 inorder: 7 4 2 5 1 8 6 9 3 
 postorder: 7 4 5 2 8 9 6 3 1 
 level-order: 1 2 3 4 5 6 7 8 9

[edit] Ursala

Ursala has built-in notation for trees and is perfect for whipping up little tree walking functions. This source listing shows the tree depicted above declared as a constant, followed by declarations of four functions applicable to trees of any type. The main program applies all four of them to the tree and makes a list of their results, each of which is a list of natural numbers. The compiler directive #cast %nLL induces the compile-time side effect of displaying the result on standard output as a list of lists of naturals.

 tree = 

 1^:< 
 2^: <4^: <7^: <>, 0>, 5^: <>>, 
 3^: <6^: <8^: <>, 9^: <>>, 0>> 

 pre = ~&dvLPCo 
 post = ~&vLPdNCTo 
 in = ~&vvhPdvtL2CTiQo 
 lev = ~&iNCaadSPfavSLiF3RTaq 

 #cast %nLL 

 main = <.pre,in,post,lev> tree

output:

  <
   <1,2,4,7,5,3,6,8,9>,
   <7,4,2,5,1,8,6,9,3>,
   <7,4,5,2,8,9,6,3,1>,
   <1,2,3,4,5,6,7,8,9>>

[edit] zkl

 class Node{ var [mixin=Node]left,right; var v; 
 fcn init(val,[Node]l=Void,[Node]r=Void) { v,left,right=vm.arglist } 
  } 

 class BTree{ var [mixin=Node] root; 
 fcn init(r){ root=r } 
 const VISIT=Void, LEFT="left", RIGHT="right"; 
 fcn preOrder { traverse(VISIT,LEFT, RIGHT) } 
 fcn inOrder { traverse(LEFT, VISIT,RIGHT) } 
 fcn postOrder { traverse(LEFT, RIGHT,VISIT) } 
 fcn [private] traverse(order){ //--> list of Nodes 
 sink:=List(); 
 fcn(sink,[Node]n,order){ 
 if(n){ foreach o in (order){ 
 if(VISIT==o) sink.write(n); 
 else self.fcn(sink,n.setVar(o),order); // actually get var 
  }} 
 }(sink,root,vm.arglist); 
 sink 
  } 
 fcn levelOrder{ // breadth first 
 sink:=List(); q:=List(root); 
 while(q){ 
 n:=q.pop(0); l:=n.left; r:=n.right; 
 sink.write(n); 
 if(l) q.append(l); 
 if(r) q.append(r); 
  } 
 sink 
  } 
  }

It is easy to convert to lazy by replacing "sink.write" with "vm.yield" and wrapping the traversal with a Utils.Generator.

 t:=BTree(Node(1, 
 Node(2, 
 Node(4,Node(7)), 
 Node(5)), 
 Node(3, 
 Node(6, Node(8),Node(9))))); 

 t.preOrder() .apply("v").println(" preorder"); 
 t.inOrder() .apply("v").println(" inorder"); 
 t.postOrder() .apply("v").println(" postorder"); 
 t.levelOrder().apply("v").println(" level-order");

The "apply("v")" extracts the contents of var v from each node.

Output:

 L(1,2,4,7,5,3,6,8,9) preorder
L(7,4,2,5,1,8,6,9,3) inorder
L(7,4,5,2,8,9,6,3,1) postorder
L(1,2,3,4,5,6,7,8,9) level-order
Retrieved from "http://rosettacode.org/mw/index.php?title=Tree_traversal&oldid=193895"

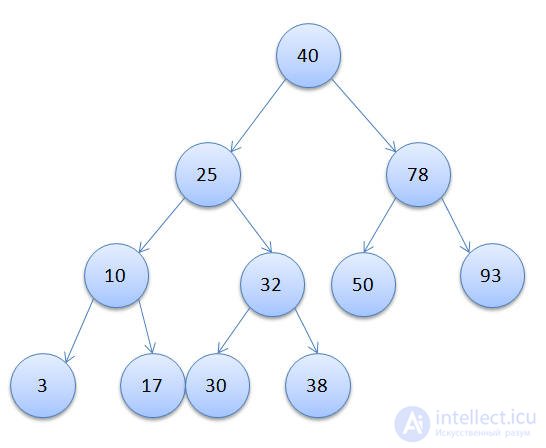
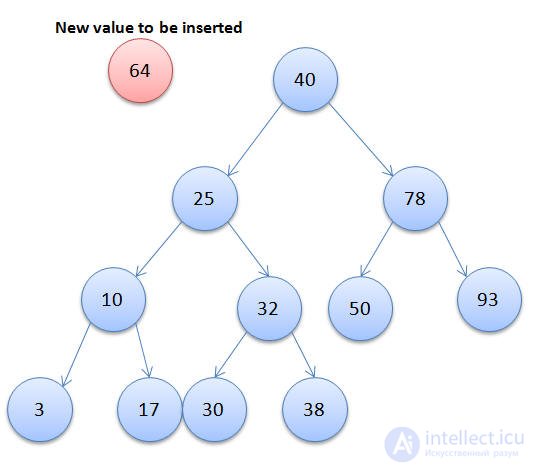
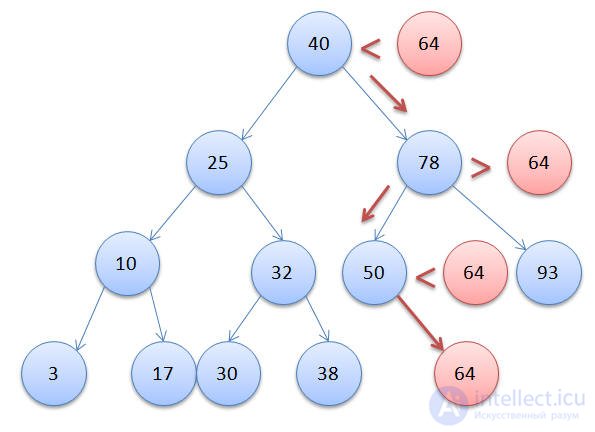
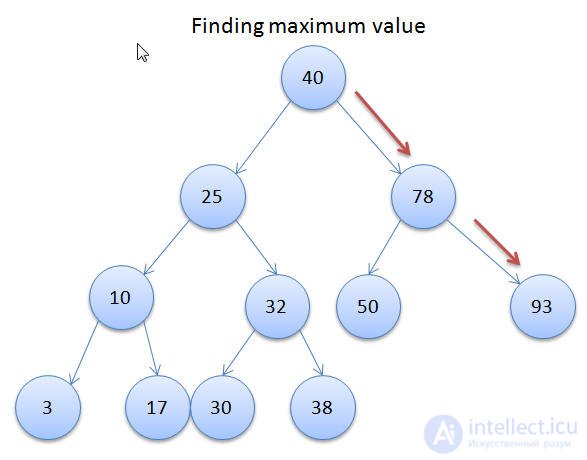
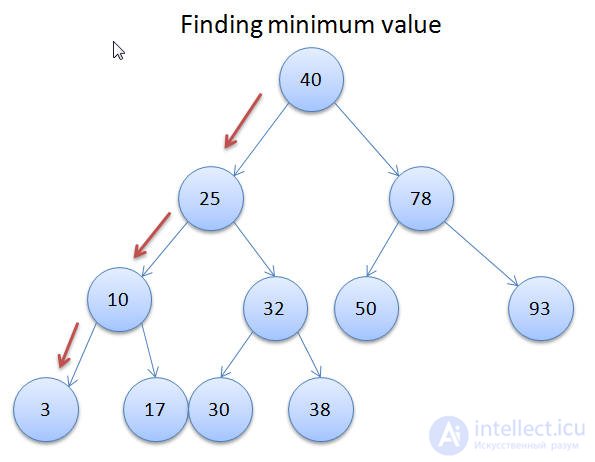
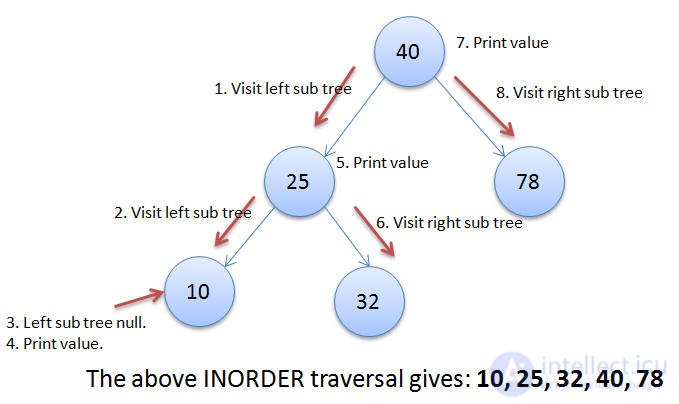
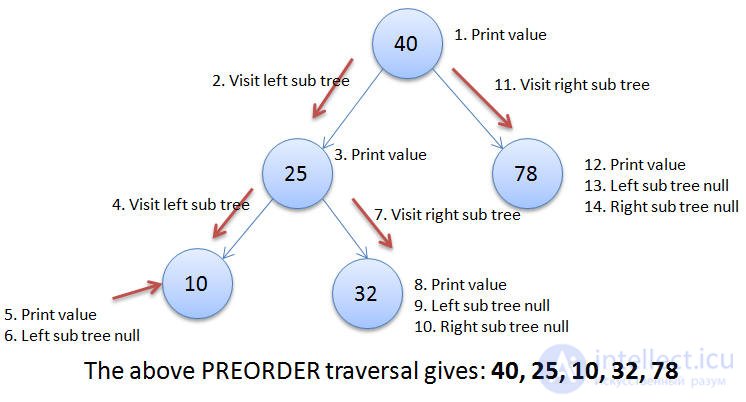
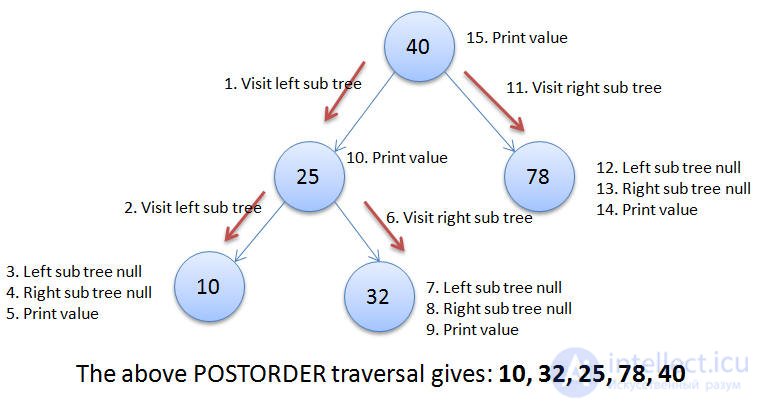
Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Structures and data processing algorithms.

Terms: Structures and data processing algorithms.