Lab number 5. "BINARY TREES (basic procedures)"

• 
  study the description of the laboratory work;

• 
  according to the task given by the teacher, to develop an algorithm for the program for solving the problem;

• 
  write a program in PASCAL;

• 
  debug the program;

• 
  to solve a task;

• 
  issue a report.

Brief theory

General information about the data structure is a tree.

A tree is a non-linear bound data structure characterized by the following features:

• 
  the tree has one element that is not referenced by other elements. This element, or "node", is called the root of the tree;

• 
  in the tree, you can access any element by passing a finite number of links (pointers);

• 
  each element of the tree is associated with only one previous element.

Each tree node can be intermediate (elements 2,3,5,7) or terminal ("leaf" of a tree) (elements 4,9,10,11,8,6). A characteristic feature of the terminal nodes is the absence of branches.





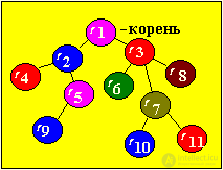
The element Y, which is directly below the element X, is called an immediate descendant of X; if X is at level i, then they say that Y lies at level i + 1.

It is believed that the root lies at level 0.

The number of direct descendants of an element is called its degree of outcome; trees are classified according to the degree of outcome of nodes of the trees:

A) If the degree of outcome of the nodes is M, then the tree is called M-ary ;

B) If the degree of outcome of the nodes is M or 0, then is a complete M-ary tree ;

C) If the degree of outcome of the tree nodes is 2, then the tree is called binary ;

D) If the degree of outcome is 2 or 0, then is a complete binary tree .

Binary trees play a particularly important role, then we will consider them in more detail.


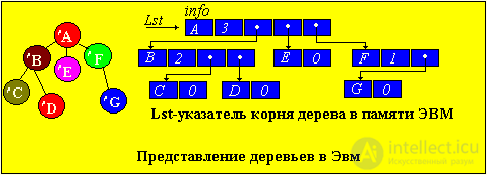
Representation of trees in computer memory


Trees are most conveniently presented in computer memory in the form of linked non-linear lists. The element must contain the INFO-field, which contains the characteristics of the site. The following field determines the degree of outcome of the node and the number of fields of pointers equal to the degree of outcome. Each element pointer orients this element node with its sons. Nodes that include arrows from the original element are called its sons.

The INFO field contains two fields: a record field (rec) and a key field (key). The key is specified by a number; the key determines the location of the element in the tree.





The reduction of the M-ary tree to the binary


1. At each node of the tree, cut off all the branches, except for the extreme left, corresponding to the eldest sons;

2. Connect the horizontal lines of the sons of one parent (node);

2. 
   The eldest son in each node of the resulting structure will be the node under the processed node.

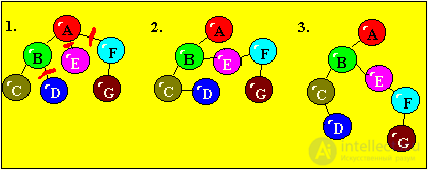
Building binary trees


According to the representation of trees in computer memory, each element (binary tree node) will be a record containing four fields. The value of these fields will be respectively the key of the record, the link to the element left-down, the element to the right-down and the text of the record.

When building it is necessary to remember that the left son has the key less than the father (the parent). The key value of the right son is greater than the key value of the father.

For example, tree nodes have the values ​​6, 21, 48, 49, 52, 86, 101.

Binary tree will look like:





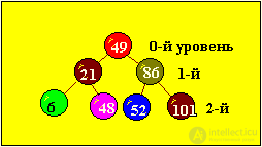
We got an ordered binary tree with the minimum number of levels.

A perfectly balanced tree is a tree in which the left and right subtrees have levels that differ by no more than one.

Algorithm

The procedure for creating a binary tree

To build a tree, it is necessary to create an element of the following type in the computer memory:





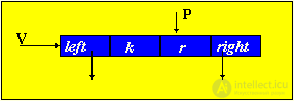
P, Q - working pointers

V = maketree (key, rec) - a procedure that creates a key and record segment

P = getnode - new item generation

r = rec

k = key

V = P

left = nil

right = nil

tree - pointer to the root of the tree

We first enter the first key value, then generate the node element of the tree using the maketree procedure. Then we go through the cycle until the pointer moves to zero.


READ (key, rec)

tree = maketree (key, rec)

WHILE not eof DO

READ (key, rec)

V = maketree (key, rec)

WHILE P <> nil DO

Q = P

IF key = k (P)

THEN P = left (P)

ELSE P = right (P)

END IF

END WHILE

IF P = nil

THEN WRITELN ('This is the root');

tree = V

ELSE IF key
THEN left (P) = V

ELSE right (P) = V

END IF

END IF

END WHILE

Tree Traversal Procedures

Let a binary tree be given:





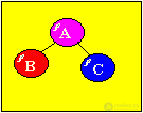
There are three principles to bypass binary trees. Consider them on the example of a given tree:

1) Top-down bypass (root is visited earlier than subtrees): A, B, C;

2) From left to right: B, A, C;

3) From bottom to top (root is visited after subtrees): B, C, A.

The second method is most often used, nodes are visited in ascending order of their key value.


Recursive tree traversal procedures:

1) PROCEDURE pretrave (tree)

IF tree <> nil

THEN PRINT info (tree)

pretrave (left (tree))

pretrave (right (tree))

END IF

RETURN

2) PROCEDURE intrave (tree)


IF tree <> nil

THEN intrave (left (tree))

PRINT info (tree)

intrave (right (tree))

END IF

RETURN

3) PROCEDURE postrave (tree)


IF tree <> nil

THEN postrave (left (tree))

postrave (right (tree))

PRINT info (tree)

END IF

RETURN

Binary Tree Search Procedure

The purpose of this procedure is to search for a node of the tree using a given key. The duration of the search operation (the number of nodes that must be searched for this purpose) depends on the tree structure. Indeed, a tree can be degenerate into a unidirectional list (have a single branch) —this tree can arise if the elements entered the tree in ascending (descending) order of their keys, for example:





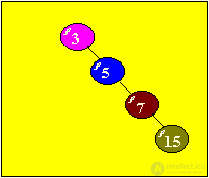
In this case, the search time will be the same as in the unidirectional list, i.e. on average, you will have to sort through N / 2 elements.

The greatest effect of using the tree is achieved in the case when the tree is "balanced". In this case, the search will have to sort through no more LOG2N elements.

We describe the search procedure. The search variable will be assigned a pointer to the found link:

p = tree

WHILE p <> nil DO

IF key = k (p)

THEN search = p

RETURN

END IF

IF key <> k (p)

THEN p = left (p)

ELSE p = right (p)

END IF

END WHILE

search = nil

RETURN

The procedure for the inclusion of an element in the tree

To include a new entry in the tree, first of all you need to find the node to which you can “hang” (attach) a new element. The algorithm for finding the desired node is the same as when searching for a node with a given key. This node will be found at the moment when, as the next link defining the branch of the tree, in which the search should be continued, the link will be NIL.

However, the search procedure described above cannot be used directly, because after the end of the calculation of its value, the node from which the NIL link was selected is not fixed.

We modify the description of the search procedure so that, as its side effect, there is a link to the node where the specified key was found (in the case of a successful search), or a link to the node after which processing the search was stopped (in the case of an unsuccessful search). And we describe the procedure for including an element in the tree, given that there is no node in the tree with the same key as the element to be included.

q = nil

p = tree

WHILE p <> nil DO

q = p

IF key = k (p)

THEN search = p

RETURN

END IF

IF key
THEN p = left (p)

ELSE p = right (p)

END IF

END WHILE

{The node with the specified key was not found, the element must be inserted. The q point indicates the prospective father's knot.}

V = maketree (key, rec)

{It is necessary to find out whether the inserted element V is the left or the right son.}

IF key
THEN left (q) = V

ELSE right (q) = V

END IF

search = V

RETURN

The procedure for removing an item from a binary tree

Deleting a node should not disrupt the ordering of the tree. When removing an element from a binary tree with a given key, three cases are distinguished:

1) the deleted node is a leaf, in this case it is simply removed without disturbing the orderliness of the tree;

2) if the deleted node has only one son, then the son moves to the place of the removed father;

4. 
   if the removed node has 2 sons. In this case, either his predecessor in a symmetrical walk (left to right) or his follower is placed in the place of the removed father.

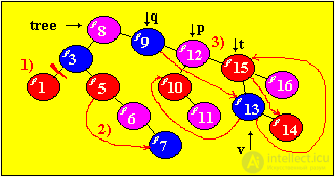
We develop an algorithm for the 3rd case (the node-node has 2 sons), instead of the node to be deleted, we put its receiver in a symmetric walk. The predecessor of the node to be deleted 12 is the rightmost node of the left subtree - node 11, and the receiver or follower with symmetric traversal (bypass from left to right) is the leftmost node of the right subtree - node 13.

We will use the following pointers:

p - working pointer;

q - one step behind p;

v - indicates the receiver;

t - one step behind v;

s - ahead of v by one step.


1) The procedure for finding the item we find the item to be deleted. The p pointer points to the item to be deleted.

2) Set the pointer v to the node that will replace the element to be deleted.

IF left (p) = nil

THEN v = right (p)

ELSE IF right (p) = nil

THEN v = left (p)

ELSE t = p

v = right (p)

s = left (v)

WHILE s <> nil

t = v

v = s

s = left (v)

END WHILE

IF t <> p

THEN WRITE (v is not a son of p)

left (t) = right (v)

right (v) = right (p)

END IF

left (v) = left (p)

IF q = nil

THEN WRITE (v root)

tree = v

RETURN

END IF

IF p = left (q)

THEN left (q) = v

ELSE right (q) = v

END IF

END IF

END IF

FREENODE (p) (the procedure creates a free node, i.e., clears the memory cell in which the deleted item is located)

RETURN

Tasks

Options:

1. Describe a procedure or function that:

a) assigns to the parameter E a record from the leftmost leaf of a non-empty tree T (a vertex leaf from which no branch leaves);

b) determine the number of occurrences of the entry E in the tree T.


2. Tree tops are real numbers. Describe a procedure or function that:

a) calculate the arithmetic average of all tree vertices;

b) add a vertex to the tree with the value calculated in the previous procedure (function).


3. Records of tree tops - real numbers. Describe a procedure that removes all vertices with negative entries.


4. Records of tree tops - real numbers. Describe a procedure or function that:

a) find the maximum or minimum value of the vertex records of a non-empty tree;

b) prints entries from all leaves of the tree.


5. Describe a procedure or function that:

a) determines whether the vertex with the record E is in the tree T;

b) if such a record is not found, then it is added.


6. Describe a procedure or function that:

a) find the length (number of branches) of the path from the root to the nearest vertex with the record E in a non-empty tree T; if E is not included in T, then take -1 for the answer.

b) determines the maximum depth of a non-empty tree T, i.e. the number of branches in the longest of the paths from the root of the tree to the leaves.


7. Describe the procedure COPY (T, T1), which builds T1 - a copy of the tree T.


8. Describe the procedure ЕQUAL (T1, T2), which verifies the equality of trees T1 and T2 (trees are equal if the keys and records of the vertices of one tree are equal respectively to the keys and records of another tree).


9. Describe a procedure or function that:

a) prints nodes of a non-empty tree when traversing from left to right;

b) removes all the leaves of the source tree;

c) prints a modified tree.


10. Describe the procedure that:

a) assigns the variable b of type char a value:

K - if a vertex is a root,

П - if a vertex is an intermediate vertex,

L - if the vertex is a leaf;

b) prints the attributes of all the vertices of the tree.


11. Describe a procedure or function that:

a) inserts the node with the record E in the tree, if this was not previously;

b) remove it if it already exists.


12. Describe a procedure or function that:

a) prints a tree found in the tree once;

b) prints the entry found in the tree the maximum number of times.