Lecture
The concept of " lists " includes a variety of data structures. It can be arrays, including arrays of records, and special dynamic data structures, and even trees. What they have in common is that they contain a set of records of one kind, limited in size or unlimited, ordered or unordered. The data stored in these records are usually logically related, for example, the names of students in the same group, etc. In the text of the program, such a connection can be expressed in the fact that all such elements are stored in the same array as a continuous block of memory. But apart from the common name of the array (and the address of its beginning) between these elements there is no other physical connection, and at the physical level such lists can be called " unrelated " (or, which is (almost) the same, " unrelated "). Those. there are no connections within them (their elements are not physically connected to each other).
A typical example of a non-persistent (physically) list is an array. In this chapter, we will look at the very "special dynamic data structures" that are called the coherent lists .
Recall the common features of queues and stacks:
Linked lists are free from these restrictions. They allow flexible access methods; extracting (reading) an item from the list does not remove it from the list or lose data. To actually remove an item from a linked list, a special procedure is required.
Linked lists are (as already mentioned) dynamic (in fact, linear!) Data structures ( dynamic chains of links ), in which the same type of elements (links) are somehow connected with each other, usually at the physical level. The connection between the elements can be achieved by storing the address of another of the same element (of the same type) in one element. Those. each information element contains within itself a pointer to its own type. Given that in addition to this pointer must be present useful data, the type of information element is a record . For example, for the simplest type of list, this type may be the following (in C / C ++ languages):
struct Link1
{
int data;
Link1 * next;
};
Classification of linked lists . By the number of links (and at the same time, direction ), the lists are simply connected (unidirectional), doubly connected (bidirectional), and multiply connected .
By the way links are organized (or by architecture ), the lists can be linear and circular (cyclic). (If the list is neither linear nor circular, then the only option left is a branch list, which is actually one of the tree data structures.)
According to the degree of ordering of the stored data, the lists can be ordered and unordered . Such a separation is sometimes convenient in practice, but in order to maintain the orderliness of the lists, it is necessary to resort to special measures.
For lists, compared with queues and stacks, there are significantly more operations , which include:
Consider the main of these operations for each type of list separately, along with the features of these types of lists.
A linear, simply linked list is the simplest type of linked list. Such a list can be defined using type descriptions (see Example 1).
Procedures for working with a linear singly-connected list in Pascalrel1 = ^ elem; (* Record pointer *) elem = record next: rel1; data: <type of stored data> (* Any valid data type *) end; var L1: rel1;  In order for operations such as adding or removing a link to be performed in the same way, regardless of where they are performed in the list, it is convenient to use a leading or a title link — the very first link in the list that does not have to store useful data. It can be created for a simply linked list as follows: var a, L1: list1; begin ... new (L1); L1 ^ .next: = nil; a: = L1; ... A pointer to the beginning of the list L1 , whose value is the address of the leading link, represents the list as a single program object. The pointer to the next element in the last link of the list is nil ( NULL or just 0 in C / C ++), which is a sign of a linear list. procedure insert1 (link: rel1; info: <Type>); var q: rel1; begin new (q); q ^ .data: = info; q ^ .next: = link ^ .next; link ^ .next: = q end; procedure delete1 (link: rel1); var q: rel1; begin if link ^ .next <> nil then begin q: = link ^ .next; link ^ .next: = link ^ .next ^ .next; dispose (q); end end; function search1 (l: rel1; info: <type>; var r: rel1): boolean; var q: rel1; begin search1: = false; r: = nil; q: = l ^ .next; while (q <> nil) and (r <> nil) do begin if q ^ .data = info then begin search: = true; r: = q end; q: = q ^ .next end end; |
The procedures for adding and removing links are critical in terms of maintaining the integrity of the list. If these procedures are performed incorrectly (i.e., if the assignment operations are incorrectly sequenced), 2 erroneous situations are possible:
1. The list "breaks" at the place of insertion or deletion of a link, and the link that turned out to be the last closes either on itself (most often) (i.e., the next or similar indicator in this link receives the address value of the same link), or to one of the previous links (depending on the incorrect implementation of the operations of insertion or deletion of the link). When you try to view the list, the viewing procedure loops and infinitely displays the contents of the same link (or several links).
2. The list also "breaks" at the place of insertion or deletion of a link, but the pointer in the link that became the last receives some arbitrary value, which is interpreted as the address of the next link (not really existing), which also has a pointer next , containing some address, and so on, until you accidentally hit a data block for which the next pointer is not zero . When you try to view a list, the correct data is displayed first, and then a random set of characters.
In both cases, the links in the “detached” part (“tail”) of the list are no longer accessible, and the data stored in them can be considered lost.
In order to prevent the occurrence of such errors, one should follow the correct order of communication (i.e. assigning pointers) when inserting a new link and deleting an existing link (the sequence of operations is indicated):
The ability to move through a 1-linked list in one direction only leads to the fact that when a link is deleted, it is not the link that is actually deleted, but the one that precedes it. This is done so that it is possible to adjust the connection for the previous link, to which it is impossible to get to the distance from the deleted one. |
One of the most simple operations with all types of lists is their passage , i.e. get access to all items one by one. We present a procedure that implements this operation for viewing the list (other options for using a walkthrough are searching for data and saving the list to a file). In the case of moving along a 2-link list in the "forward" direction, this procedure is the same for 1- and 2-link linear lists.
void Show (Link1 * link) { Link1 * q = link-> next; // Take into account the presence of "empty" lead while (q) // or while (q! = NULL) { cout << q-> data << ''; // or another operation q = q-> next; // Go through the list } cout << endl; } |
Search in the list is a variant of the operation of viewing and differs in that
1. instead of the screening operation (cout << q-> data), the operation of comparing the desired data with those stored in the links of the list is used;
2. If the required data is found, there is no need to move further in the list.
A search in single-linked lists has the following feature. If it is performed in conjunction with deletion, then the search result may (or should) be not the link in which the search data is contained, but the one preceding it. As a result, the search in the list may require either two different procedures — the “usual” and finding the previous link, or one universal one that allows you to find both links — with the data you are looking for and preceding it. Consider this as an example.
int Search (Link1 * Start, // Starting Point Link1 * & Find, // Pointer to the link with the desired data Link1 * & Pred, // Pointer for the previous link int Key) // Search Key { Link1 * Cur = Start-> next; // Current Link Pred = Start; // Previous link ("lags behind" by 1 step from the current one) int Success = 0; // Sign of success of the search (set to 0) while (Cur &&! Success) // Boolean operation "And" { if (Cur-> data == Key) // found { Find = cur; // Memorizing Found Link Success = 1; // Set to 1 sign of success break; // Exit the loop when searching successfully } Pred = Cur; // Move the previous link Cur = Cur-> next; // Go forward through the list } return success; } It should be noted that different (including shorter) variants of the implementation of such an algorithm are possible, for example, without the Success variable (the Find pointer is used instead, which, before starting the search, should receive a NULL value and save it if the search was unsuccessful). The procedure that finds only the link being searched for is simpler - it does not need the pointer Pred and all the operators in which it is used. A similar procedure applies for a 1-linked ring list. Its difference from the considered example lies in the condition of continuing the loop in the while statement: while (Cur! = Start &&! Success) // For the ring list |
Leading (or title) link. All the above examples in the C ++ language imply the presence of a leading link in the list. This link can be created either by a separate procedure or by the following set of operators (the same operators will be in the procedure):
Link1 * L1 = new Link1; // Memory allocation under the link
L1-> next = NULL; // Lead link at the same time is the last
It is possible to work with a linked list and without a dedicated lead, i.e. The first link is normal, it contains useful data. This kind of list was used for organizing the stack. Another example of using such lists is the queue .
void queue_in (Link2 * & q, // Head of the queue Link2 * & e, // "Tail" queue int k) // Input { Link2 * n = new node; // New node n-> data = k; n-> next = q; if (q) q-> prev = n; else e = n; n-> prev = 0; q = n; } int queue_out (Link2 * & q, Link2 * & e) { int k = e-> data; Link2 * d = e; e = d-> prev; if (e) e-> next = 0; else q = e; delete d; return k; } To simplify the processing of the "head" and "tail" of the queue, a 2-linked list is used. |
In other cases (i.e., for regular lists), the use of a leading link is preferable, since Avoids checks when adding and removing links.
The disadvantages of a single-linked list are as follows:
1. In this list, you can move only from the initial link to the final link. You can start from any link in the list, but if you suddenly need to refer to the previous elements, you will have to start from the initial link, which is inconvenient, irrational and complicates the data processing algorithms.
2. The presence of only one connection reduces the reliability of data storage in a 1-linked list.
3. The consequence of the first drawback is the complication of the interaction of search and delete operations.
The advantages of this list are less memory consumption compared to other intrusive dynamic data structures (only 1 pointer) and simplicity of operations.
This list is free from the drawbacks of a single-linked list. To this end, one additional pointer has been added to each link to the type of link whose value is the address of the previous link in the list. Link type in C / C ++ languages:
struct Link2
{
int data;
Link2 * next, * prev;
};
The structure of the list will be as follows (the values of null pointers are shown for Pascal):
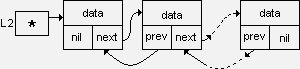
The leading link of this list is created by the following set of operators:
Link2 * L2 = new Link2;
L2-> next = NULL;
L2-> prev = NULL;
According to the operators of the creation of the leading link, one can judge whether the list is 1- or 2-connected, linear or circular. The zero values of the next and prev pointers are a sign of a linear list.
Graphically, the status of the list after creating the lead can be displayed as follows:
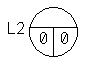
Advantages of a doubly linked list:
Operations with a 2-linked list. Everything related to the operations of adding a link and its removal for a 1-linked list is also true for a 2-linked one. Also, the correct order of conducting (or deleting) links between the links should be observed, but there are more such operations, because 2 pointers must be processed. In addition, each of the operations has additional features:
1. When adding a new link to an empty list, i.e. containing only the leading link (see the previous figure), or when adding a link to the end of the list (for an empty list, both these situations coincide), you must check the presence of a link that will be next to the one being added (for an empty list or end of the list there is no such link, which means there is no pointer indicating a link). The same check should be performed when deleting a link.
2. The ability to move through the list in both directions allows you to directly specify the link to be deleted (and not the previous one, as in a 1-linked list). The consequence of this is to simplify both the delete operation and the search operation.
void Insert2 (Link2 * St, int data) { Link2 * q = new Link2; // 1 Memory allocation for the link q-> data = data; // 2 Data Entry q-> next = St-> next; // 3 Conduct communication from the new link forward q-> prev = St; // 4 Conduct communication from the new link back St-> next = q; // 5 Conduct communication from the previous link to the new if (q-> next) // Check for the presence of the next link q-> next-> prev = q; // 6 Conduct communication from the next link to the new } void Delete2 (Link2 * del) { del-> prev-> next = del-> next; // 1 processing communication forward if (del-> next) del-> next-> prev = del-> prev; // 2 Processing link back delete del; // 3 Memory free } int Search2 (Link2 * Start, Link2 * & Find, int Key) { Link2 * Cur = Start-> next; int Success = 0; while (Cur &&! Success) { if (Cur-> data == Key) { Find = cur; Success = 1; break; } Cur = Cur-> next; } return success; } This search procedure is actually (with the exception of the data type Link2 instead of Link1 ) a "normal" search procedure (that is, not for deletion) in a 1-linked list. |
The operation of viewing the list in the forward direction is no different from viewing the 1-linked list.
If the value of the pointer of the last link of a linear singly list is replaced with nil (or NULL ) with the address of the leading link, then the linear list will turn into a simply-connected ring list.
For a doubly linked list, in addition, you need to replace with nil with the address of the last link the value of the second pointer in the lead link. The result is a doubly connected ring (cyclic) list.
In a simply-connected ring list, you can go from the last link to the title link, and in the doubly linked list, you can also move from the title link to the last link.
The doubly-connected ring list looks like this:
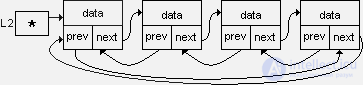
A ring list, as well as a linear one, is identified as a single program object by a pointer, for example, L2 , whose value is the address of the title link.
There is another option for organizing a ring list:
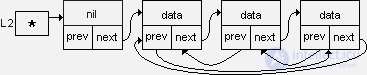
Both options are comparable in complexity. For the first option, it is easier to insert a new element both at the beginning of the list (after the title link) and at the end - since inserting a link at the end of the ring list is equivalent to inserting before the title link, but each time the list is cyclically processed, it’s necessary to check whether the current link in the title (or whether the current link does not coincide with the starting point of processing).
Consider operations with ring lists .
The absence of the “last” link leads to an even greater simplification of the operations of adding and deleting, as compared with a 1- and 2-connected linear list. For example, for a 1-linked ring list there is no if statement in the deletion procedure — a check for the existence of a link following the specified one (there is always such a link in the ring list).The same operators are missing in the procedures for adding and deleting links for a 2-connected ring list.
When cyclically processing a ring list, you need to consider that formally there is no last link.
Work program with a doubly-connected Pascal ring listrel2 = ^ elem2; elem2 = record next: rel1; prev: rel2; data: <type of stored data> end; list2 = rel2; procedure insert2 (pred: rel2; info: <type>); var q: rel2; begin new (q); (* Creating a new link *) q ^ .data: = info; q ^ .next: = pred ^ .next; q ^ .prev: = pred ^ .next ^ .prev; pred ^ .next.prev: = q; pred ^ .next: = q end; When inserting at the beginning of the list (after the title link), you must specify the address of the title link, that is, a pointer to the L2 list, as the pred argument . procedure delete2 (del: rel2); begin del ^ .next ^ .prev: = del ^ .prev; del ^ .prev ^ .next: = del ^ .next; dispose (del); end; function search2 (list: rel2; info: <type>; var point: rel2): boolean; var p, q: rel2; b: boolean; begin b: = false; point: = nil; p: = list; q: = p ^ .next; while (p <> q) and (not b) do begin if q ^. data = info then begin b: = true; point: = q end; q: = q ^ .next end; search2: = b end; ... ... var l2: list2; r: rel2; begin (* Create title link *) new (r); r ^ .next: = r; r ^ .pred: = r; l2: = r; ... ... end. Procedures for working with a doubly-connected C ++ ring listThe data type for a ring 2-link list is the same as for a 2-link linear. The same is true for 1-linked lists. According to the type of a link in the list, one cannot judge its architecture ; it is possible only about the number of links . Adding a link to an arbitrary position behind the lead link{ Link2 * Loc = new Link2; // 1 Loc-> Value = data; // 2 Loc-> next = Pred-> next; // 3 Loc-> prev = Pred; // 4 Pred-> next = Loc; // 5 Loc-> next-> prev = Loc; // 6 } Remove a link from anywhere in the list for a leading link{ Del-> prev-> next = Del-> next; // 1 Del-> next-> prev = Del-> prev; // 2 delete Del; // 3 } Search{ Link2 * Cur = Start-> next; int Success = 0; while (Cur! = Start &&! Success) { if (Cur-> Value == Key) { Find = cur; Success = 1; break; } Cur = Cur-> next; } return success; } The search termination in case of failure occurs when the “current” Cur pointer reaches the Start search point , i.e. if the condition in the while statement is not met : while (Cur! = Start ...) |
The leading link of the ring 2-linked list is created by a set of operators:
Link2 * L2 = new Link2;
L2-> next = L2;
L2-> prev = L2;
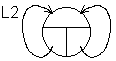
Graphically, the state of the list after creating this link can be represented as follows:
Multi-linked lists are dynamic data structures based on 1- or 2-linked lists that have additional links between links. Most often, such links are made between distant links, for example, denoting categories of data. An example of a multiply linked list is shown in the following figure.

The transition between links AA and BA can be performed by additional communication, bypassing links AB and AB. Because of this type of movement, these lists are sometimes called skip lists (skip - jump over). And with the nature of data placement, similar to that shown in this figure, such lists are called dictionary (sometimes just dictionaries , but the term “dictionary” can be used in the theory of data structures in different meanings).
single-linked linear list
================
struct Link1
{
int value;
Link1 * next;
};
linear:
=========
Link1 * L1 = new Link1;
L1-> next = NULL;
Adding a link to an arbitrary position behind the lead link:
void Insert (Link1 * Pred, int data)
{
Link1 * Loc = new Link1;
Loc-> Value = data;
Loc-> next = Pred-> next;
Pred-> next = Loc;
}
Removing a link from anywhere in the list for the lead link:
void Delete (Link1 * Pred)
{
Link1 * Loc;
if (Pred-> next)
{
Loc = Pred-> next;
Pred-> next = Loc-> next;
delete Loc;
}
}
Universal search procedure (finds a link with a search key
and preceding it):
int Search (Link1 * Start, Link1 * & Find, Link1 * & Pred, int Key)
{
Link1 * Cur = Start; // -> next;
Pred = Start;
int Success = 0;
while (Cur &&! Success)
{
if (Cur-> Value == Key)
{
Find = cur;
Success = 1;
break;
}
Pred = Cur;
Cur = Cur-> next;
}
return success;
}
List reversal
=================================
- with "while" loop
void ReverseW (Link1 * L)
{
Link1 * a = L-> next, * b = a, * c = NULL;
while (b)
{
a = b;
b = a-> next;
a-> next = c;
c = a;
}
L-> next = a;
}
Link1 * ReverseW1 (Link1 * L)
{
Link1 * a = L-> next, * b, * c = NULL;
while (a)
{
b = a-> next;
a-> next = c;
c = a;
a = b;
}
return c;
}
- with "for" loop
void Reverse (Link1 * L)
{
Link1 * a = L-> next, * b = a, * c = NULL;
for (; b; a = b, b = a-> next, a-> next = c, c = a);
L-> next = a;
}
Link1 * Reverse1 (Link1 * L)
{
Link1 * a = L-> next, * b, * c = NULL;
for (; a; b = a-> next, a-> next = c, c = a, a = b);
return c;
}
Sorting
==========
Bubble:
------------
- with removal and addition procedures
void BubbleListSort (Link1 * Start)
{
int buf, n = 0;
Link1 * Last, * b, * b0;
for (Last = NULL; Last! = Start-> next;)
{
for (b0 = Start, b = Start-> next; b-> next! = Last; b0 = b0-> next)
{
if (b-> Value> b-> next-> Value)
{
buf = b-> next-> Value;
Delete (b);
Insert (b0, buf);
}
else
b = b-> next;
}
Last = b;
}
}
- with the replacement of pointer values
void Bubble2ListSort (Link1 * Start)
{
int n = 0;
Link1 * Last, * b, * b0;
for (Last = NULL; Last! = Start-> next;)
{
for (b0 = Start, b = Start-> next; b-> next! = Last; b0 = b0-> next)
{
if (b-> Value> b-> next-> Value)
{
b0-> next = b-> next; // Rearrange links
b-> next = b-> next-> next;
b0-> next-> next = b;
}
else
b = b-> next;
}
Last = b;
}
}
- with transfer of data between links
void BubbleListSortSimple (Link1 * Start)
{
Link1 * q;
int buf, n = 0;
for (Link1 * Last = NULL, * e = Start-> next; e-> next; e = e-> next)
{
for (q = Start-> next; q-> next! = Last; q = q-> next)
{
if (q-> Value> q-> next-> Value)
{
buf = q-> Value;
q-> Value = q-> next-> Value;
q-> next-> Value = buf;
}
}
Last = q;
}
}
Sort by selection:
-------------------
- analog of array sorting with addition and removal procedures
void SelectSort (Link1 * Start)
{
int min, change, n = 0;
Link1 * Beg, * predmin, * b;
for (Beg = Start; Beg-> next; Beg = Beg-> next)
{
change = 0;
min = Beg-> next-> Value;
for (b = Beg; b-> next; b = b-> next)
{
if (b-> next-> Value <min)
{
min = b-> next-> Value;
predmin = b;
change = 1;
}
}
if (change)
{
Delete (predmin);
Insert (Beg, min);
}
}
}
- with the replacement of pointer values
void Select1 (Link1 * Start)
{
int min, change, n = 0;
Link1 * Beg, * predmin, * b, * Lmin;
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.