Lecture
Schematic representation of a binary tree: there is a set of vertices connected by arrows. From each vertex there are no more than two arrows (branches) directed to the left - down or to the right - down. There must be a single vertex, which does not include any arrows - this vertex is called the root of the tree. Each of the remaining vertices includes one arrow. 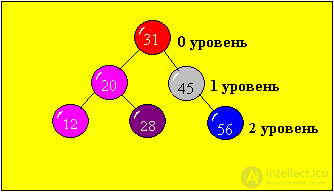
There are many ways to organize a tree. Consider one of them:
The "left" son has the key less than the key of the "Father"
The “Right” Son Has the Key More Than the “Father” Key
We obtained a binary ordered tree with the minimum number of levels.
Strongly balanced tree: a tree in which the left and right subtrees have levels that differ by no more than one.
Consider the principle of building a tree when adding elements to an array:
Let the following elements be entered into the initially empty array: 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86; Because it is still an empty tree, the links left and right are equal to nil (left is a pointer to the left son (element), right is a pointer to the right son (element)).
The fourth of the incoming items 87. Because Since this key is larger than key 70 (root), then a new vertex must be placed on the right branch of the tree. To determine its place, we go down the right arrow to the next vertex (with key 85), and if the received key is greater than 85, then we make the vertex with the key 85 with the right son. 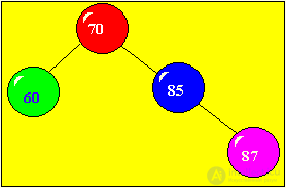
In the considered example, the PRINCIPLE of TREE CONSTRUCTION has the following form: if the next element of the array arrives, then starting from the root of the tree (depending on the comparison of the current element with the next vertex), go to the left or right of it until we find a suitable vertex to which You can connect a new vertex with the current key. Depending on the result of comparing the keys, we make a new vertex left or right for the found vertex.
To create a tree, you need to create an element of the following type in memory: 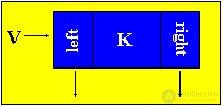
PASCAL Type:
type
pelem = ^ elem;
elem = record
left: pointer;
right: pointer;
K: integer;
end;
K is an array element, V is a pointer to the created element.
The following pointers will be used in the procedure for creating a binary search tree:
tree - pointer to the root of the tree;
p - working pointer;
q - pointer lagging one step from p;
key - new element of the array;
(pseudocode)
writeln ('Enter an array element');
readln (key);
tree: = maketree (key);
p: = tree;
while not eof do
begin
readln (key);
v: = maketree (key);
while p <> nil do
begin
q: = p;
if key <k (p) then = "" p: = "left (p) <br">
else p: = right (p);
end;
if p = nil then
begin
writeln ('This is the root');
tree: = v;
end
else
if key <k (q) then = "" left (p): = "v <br">
else right (p): = v;
end;
When traversing a tree from left to right, we get a sorted array of 20, 30, 35, 45, 60, 70, 82, 85, 86, 87, 88, 90. The tree element is entered into the array during the second entry into it (in the figure, the second visits are shown in green arrows). 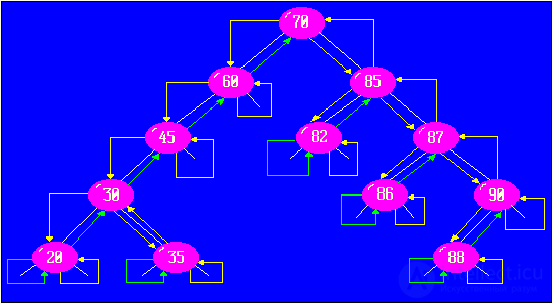
procedure InTree (tree);
begin
if Tree = nil then write ('Tree is empty')
else
with Tree ^ do
begin
if left <> nil then InTree (left);
if right <> nil then InTree (right);
end;
end;
Option 1: The factory produced parts with the following serial numbers: 45, 56, 13, 75, 14, 18, 43, 11, 52, 12, 10, 36, 47, 9. Parts with even numbers go to warehouse number 1, And with odd on sweet №2. Required to sort the parts in stock number 1.
Option 2: Car hijacked. The witness remembered that the first digit of the number was 4. The following numbers were in the base of stolen cars that day: 456, 124, 786, 435, 788, 444, 565, 127, 458, 322, 411, 531, 400, 546, 410 It is necessary to make a list of numbers starting with 4 and sort it in ascending order.
Option 3: For a week away, tickets with numbers 124512, 342351, 765891, 453122, 431350, 876432, 734626, 238651, 455734, 234987 have accumulated in the transport. You need to select the "happy" tickets and arrange them in ascending order.
Option 4: Given a list of people with their age. For scheduling retirement of employees, it is required to compile a new list in the order in which they will retire.
Option 5: Students passed five exams. It is necessary to sort the list of students by increasing the total score on the results of exams.
Option 6: There was one bus fleet in the city, where buses with the numbers 11, 32, 23, 12, 6, 52, 47, 63, 69, 50, 43, 28, 35, 33, 42, 56, 55, 101. After the construction of the second fleet, they decided to transfer there buses with odd numbers. In order to schedule their movement you need to organize a list of bus numbers of the second park, ordering them in descending order.
Option 7: A salary statement was drawn up, presented in the form: Ivanov - 166000, Sidorov - 180000, ... It is required to organize this list in such a way that the size of the salary decreases.
Option 8: There are cars with the following numbers on the parking lot: 1212, 3451, 7694, 4512, 4352, 8732, 7326, 2350, 4536, 2387, 5746, 6776, 4316, 1324. For statistics it is necessary to make a list of vehicles with such numbers, the amount the first two digits of which is equal to the sum of the last two digits, so that each next number is less than the previous one.
Option 9: Issued lottery tickets with four-digit numbers. Winning are those tickets whose sum of digits is divided by 4. Make a list of winning tickets, ordered in descending order.
Option 10: The young man took the phone number from his friend, but forgot it. He could only remember the first three digits: 469 ***. In his notebook were the following phone numbers: 456765, 469465, 469321, 616312, 576567, 469563, 567564, 469129, 675665, 469873, 569090, 469999, 564321, 469010. Make a list of numbers starting with 469 and sort them in descending order.
Option 11: Students have passed five exams. It is necessary to sort the list of students descending the total score on the results of exams.
Option 12: Issued lottery tickets with four-digit numbers. Winning are those tickets, the sum of the first three digits of which is equal to 8. Make a list of winning tickets, arranged in ascending order.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.