Lecture
Data structures are a collection of data elements and relationships between them. In this case, data elements can be understood as a simple given and a data structure. The relationship between the data means the functional relationships between them and pointers to where the data is located.
Graphic representation of the data structure element.
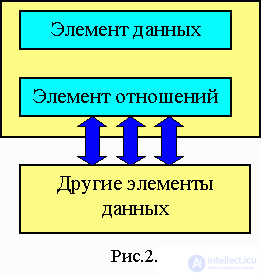
An element of relations is a collection of all links of an element with other data elements of the structure under consideration.
S: = (D, R)
Where S is the data structure, D is the data and R is the relationship.
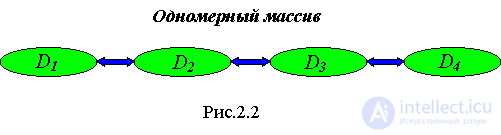
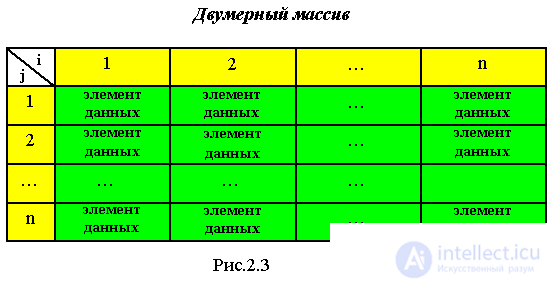
No matter how complex the data structure may be, in the end it consists of simple data (see Fig. 2.2, 2.3).
The inner world of computers is not as simple as we think. The memory of the machine consists of millions of triggers that process the incoming information.
We, bringing information to the computer, present it in some form, which in our opinion organizes the data and gives them meaning. The machine takes the field for incoming information and gives it some address. Thus, it turns out that we process data at a logical level, as if in an abstract way, and the machine does it at a physical level.
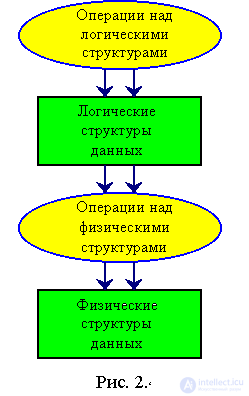
The sequence of transitions from logical to physical organization is shown in Fig. 2.4.
Data structures are classified:
1. By data coherence in the structure:
- if the data in the structure is connected very weakly, then such structures are called unbound (vector, array, rows, stacks)
- if the data in the structure is related, then such structures are called linked (linked lists)
2. According to the variability of the structure in time or in the process of program execution:
- static structures - structures that do not change until the end of the program (records, arrays, strings, vectors)
- semi-static structures (stacks, decks, queues)
- dynamic structures - a complete change occurs during program execution
3. By the orderliness of the structure:
- linear (vectors, arrays, stacks, decks, records)
- nonlinear (multiply connected lists, tree structures, graphs)
The most important characteristic is the variability of the structure over time.
The simplest static structure is a vector. A vector is a purely linear ordered structure, where the relationship between its elements is a strictly expressed sequence of elements of the structure (Fig. 2.5).
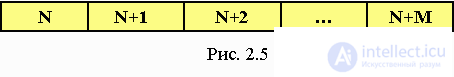
Each element of the vector has its own index, which determines the position of this element in the vector. Since indices are integers, operations can be performed on them and, thus, the position of the element in the structure at the logical access level can be calculated. To access an element of a vector, you just need to specify the name of the vector (element) and its index.
To access this element, the addressing function is used, which generates from the index value the slot address where the value of the source element is located. To declare a vector program, you must specify its name, number of elements and their type (data type)
Example:
var
M1: Array [1..100] of integer;
M2: Array [1..10] of real;
The vector consists of completely the same type of data and their number is strictly defined.
In the general case, an element of an array is an element of a vector, which itself is also an element of a structure (Fig. 2.6).
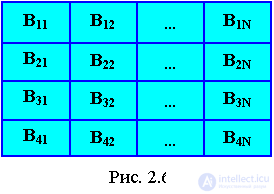
To access an element of a two-dimensional array, the values of a pair of indices are needed (row number and column number, at the intersection of which the element is located). At the physical level, a two-dimensional array looks the same as a one-dimensional (vector), and translators represent arrays either as rows or as columns.
A record is a data structure of a sequential type, where the elements of a structure are arranged one after the other in both logical and physical representation. Writing involves many elements of a different type. Data elements in a record are often called record fields.
Example:
The logical structure of the record can be represented both graphically and in tabular.

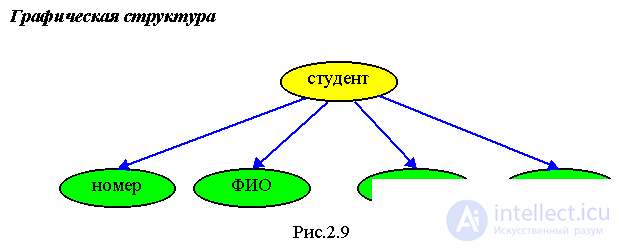
The entry element may include entries. In this case, a complex hierarchical data structure arises.
Example:
It is necessary to fill out a student record containing the following information: N - the student’s sequence number; The name of the student, which should include: Last Name, First Name; Student profile data: year of birth, place of birth, parents: mother, father; Faculty; Group; Estimates received in the session: in English and microprocessors.
Below are two logical representations of the structure of this record.
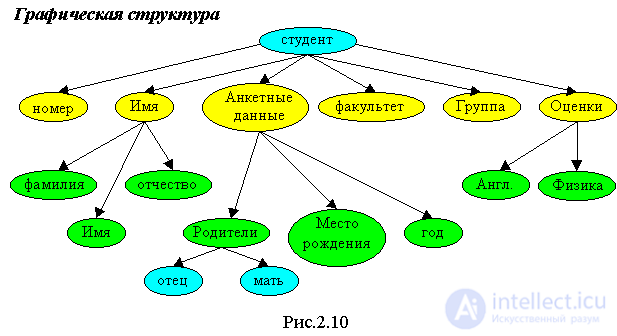
A four-level hierarchical data structure was obtained. Information is contained in the leaves, the remaining nodes are used to indicate the path to the leaves.
1st level Student = entry
2nd level Room
2nd level Name = entry
3rd level Last Name
3rd level Name
3rd level Middle Name
Level 2 Profile Data = Record
3rd level Place of birth
3rd level Year of birth
3rd level Parents = record
4th level Mother
4th level Father
Level 2 Faculty
Level 2 Group
Level 2 Rating = entry
3rd level English
3rd level Physics
This structure is called a nested record.
Record operations:
A table is a final set of records (Fig. 2.11).

When setting a table, the number of records contained in it is indicated.
Example:
Type ST = Record
Num: Integer;
Name: String [15];
Fak: String [5];
Group: String [10];
Angl: Integer;
Physic: Integer;
var
Table: Array [1..19] of St;
The data element of the table is a record. Therefore, operations that are performed with a table are operations performed with a record.
Operations with tables:
1. Search for a record by a given key.
2. Making a new entry in the table.
The key is the record ID. A special field is reserved for storing this identifier.
Composite key - a key containing more than two fields.
Semi-static data structures include stacks, decks, and queues.
Lists
This is a set of related data elements, which in general can be of different types.
Example list:
E 1 , E 2 , ........, E n , ... n> 1 and not fixed.
The number of items in the list may change during the execution of the program. There are 2 types of lists:
In disconnected lists, the relationship between data elements is implicitly expressed. In linked lists, a link pointer is placed in the data element with a subsequent or previous list element.
Stacks, decks and queues are inconsistent lists. In addition, they refer to sequential lists in which an implicit link is displayed by their sequence.
The queue of the form LIFO (Last In First Out - Last arrived, first left ), in which the queue element that last entered into it is the first to be selected for service, is called the stack. This is one of the most commonly used *** data structures, which turns out to be very convenient for solving various problems.
Due to the specified discipline of service, its only position in the stack, which is called the top of the stack, is the position in which the last element on the stack is located. When we push a new element into the stack, it is placed on top of the previous top and now it is already at the top of the stack. You can select an item only from the top of the stack; at the same time, the selected element is removed from the stack, and at its top is an element that was pushed onto the stack before the selected element (structure with limited access to data).
Graphically, the stack can be represented as follows:
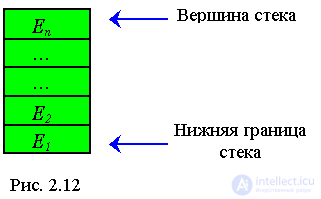
The first item goes down the stack. The stack is fetched from the top, so the stack is a structure with restricted access.
Operations performed on stacks:
Push (S, I), where S is the stack identifier, I is the entry element.
Pop (S)
Empty (S)
StackTop (S)
An example of a Pascal stack implementation using a one-dimensional array:
type
Stack = Array [1..10] of Integer; {stack with a capacity of 10 elements of type Integer}
var
StackCount: Integer; {Variable - pointer to the top of the stack, its initial value must be 0}
S: Stack; {Stack declaration}
Procedure Push (I: Integer; var S: Stack);
begin
Inc (StackCount);
S [StackCount]: = I;
end;
Procedure Pop (var I: Integer; S: Stack);
begin
I: = S [StackCount];
Dec (StackCount);
end;
Function Empty: Boolean;
begin
If I = 0 then Empty: = True Else Empty: = False;
end;
When performing a fetch operation from the stack, it is first necessary to check for stack emptiness. If it is empty, then Empty returns True. If Empty returns False, this means that the stack is not empty and you can still select elements from it.
Procedure StackTop (var I: Integer; S: Stack);
begin
I: = S [StackCount];
end;
The concept of queue is well known to everyone from everyday life. The elements of the queue in the general case are orders for a particular service.
In programming, there is a data structure called a queue. This data structure is used, for example, to simulate real queues in order to determine their characteristics for a given law of receipt of orders and the discipline of their maintenance. In its essence, the queue is a semi-static structure - with the passage of time and the queue length, and the composition may vary.
In fig. 2. 13 shows a queue containing four elements — A, B, C, and D. Element A is located at the head of the queue, and element D is at its end. Items can only be deleted from the front of the queue, that is, the first item to be placed in the queue is deleted first. For this reason, a queue is often referred to as a list organized on the principle of “the first placed first is deleted” as opposed to the principle of the stack organization — the last placed first is deleted.
The discipline of service, in which the order that entered the queue first, is selected first for service (and is removed from the queue), is called FIFO (First In First Out - First arrived, first left). The queue is open on both sides.
Thus, the removal of the component occurs from the beginning of the queue, and the write-to-end. In this case, two pointers are entered: one at the beginning of the queue, the second at its end.
A real queue is created in the computer memory as a one-dimensional array with a finite number of elements; in this case, it is necessary to indicate the type of the elements of the queue, and a variable is also needed in the work with the queue.

Physically, the queue occupies a solid area of memory and the elements follow each other, as in a sequential list.
Operations performed on the queue:
Three primitive operations are defined for the queue. The insert (q, x) operation places an element x at the end of the q queue. The remove (q) operation removes the element from the head of the queue q and assigns its value to the variable x. The third operation, empty (q), returns true or false depending on whether the queue is empty or not. Besides. Given that the semi-static queue is implemented on a one-dimensional array, it is necessary to monitor the possibility of its overflow. This goal introduces full (q).
The insert operation can always be performed, since there are no restrictions on the number of elements that the queue can contain. The remove operation, however, applies only to a non-empty queue, since it is not possible to remove an item from a queue that does not contain elements. The result of an attempt to remove an item from an empty queue is the occurrence of an exceptional loss of value. The operation empty is, of course, always possible.
An example of the implementation of the queue in the form of a one-dimensional array in Pascal:
const
MaxQ = ...
type
E = ...
Queue = Array [1..MaxQ] of E;
var
Q: Queue;
F, R: Integer;
{The F pointer points to the beginning of the queue. The R pointer points to the end of the queue. If the queue is empty, then F = 1, and R = 0 (That is, R < F is the empty condition of the queue ).}
Procedure Insert (I: Integer; var Q: Queue);
begin
Inc (R);
Q [R]: = I;
end;
Function Empty (Q: Queue): Boolean;
begin
If R
end;
Procedure Remove (var I: Integer; Q: Queue);
begin
If Not Empty (Q) then
begin
I: = Q [F];
Inc (F);
end;
end;
An example of working with the queue using standard procedures.
MaxQ = 5
We insert the elements A, B and C into the queue.
Insert (q, A);
Insert (q, B);
Insert (q, C);
Remove elements A and B from the queue.
Remove (q);
Remove (q);
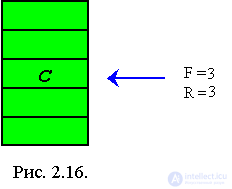
Unfortunately, with such a representation of the queue, an absurd situation may arise in which the queue is empty, but a new element cannot be placed in it (consider the sequence of deletion and insertion operations leading to this situation). It is clear that queuing with an array is unacceptable.
One solution to the problem may be to modify the remove operation so that when the next element is removed, the entire queue shifts to the beginning of the array. The remove (q) operation can be implemented in this case as follows.
X = q [1]
For I = 1 to R-1
q [I] = q [I + 1]
next I
R = R-1
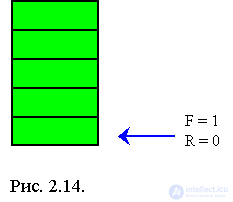
The variable F is no longer required, since the first element of the array is always the beginning of the queue. An empty queue is represented by a queue for which the value of R is zero.
However, this method is very unproductive. Each deletion requires the movement of all remaining items in the queue. If the queue contains 500 or 1000 elements, then it is obvious that this is a very inefficient way. Further, the operation of removing an item from a queue logically involves manipulating only one item, that is, the one that is located at the beginning of the queue. The implementation of this operation should reflect exactly this fact, without producing a lot of additional actions.
Another way is to consider an array that contains a queue in the form of a closed ring, rather than a linear sequence having a beginning and an end. This means that the first element in the queue immediately follows the last one. This means that even if the last element is busy, the new value can be placed immediately after it in place of the first element, if this first element is empty.
The organization of the ring queue.
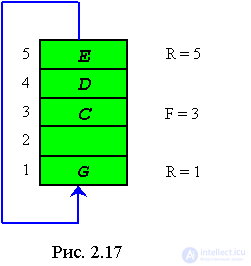
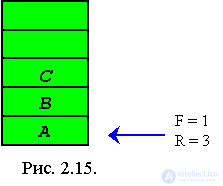
Consider an example. Suppose that the queue contains three elements - in positions 3, 4 and 5 of the five-element array. This case, shown in Fig. 2.17. Although the array is not full, the last item in the queue is busy.
If now an attempt is made to queue an element of G, then it will be written to the first position of the array, as shown in Fig. 2.17. The first element of the queue is Q (3), followed by elements of Q (4), Q (5) and Q (l).
Unfortunately, with this view it is quite difficult to determine when the queue is empty. Condition R
One way to solve this problem is to introduce an agreement in which the value of F is the index of the element of the array immediately preceding the first element of the queue , and not the index of the very first element. In this case, since R contains the index of the last element of the queue, the condition F = R implies that the queue is empty.
Note that before you start working with the queue, the value of the last array index is set to F and R, not 0 and 1, because with this representation of the queue, the last element of the array immediately precedes the first element. Since R = F, the queue is initially empty.
The main operations with the ring queue:
1. Insert the q element in the queue x.
Insert (q, x)
Remove (q)
Empty (q)
The operation empty ( q ) can be written as follows:
if F = R
then empty = true
else empty = false
endif
return
The remove ( q ) operation can be written as follows:
empty (q)
if empty = true
then print "fetching from an empty queue"
stop
endif
if F = maxQ
then F = 1
else F = F + 1
endif
x = q (F)
return
Note that the value of F must be modified before the element is retrieved.
Insert operation insert (q, x).
In order to program an insert operation, the situation in which an overflow occurs must be analyzed. Overflow occurs if the entire array is already occupied by the elements of the queue and an attempt is made to place another element in it. Consider, for example, the queue in fig. 2. 17 . It contains three elements - C, D and E, respectively located in Q (3), Q (4) and Q (5). Since the last element in the queue occupies the position Q (5), the value of R is equal to 5. Since the first element in the queue is in Q (3), the value of F is 2. In Fig.2. 17 the element G is placed in the queue, which leads to a corresponding change in the value of R. If you make the next insert, the array becomes completely filled, and an attempt to make another insert leads to overflow. This is registered by the fact that F = R, and this just indicates overflow. Obviously, with such an implementation it is not possible to make a distinction between an empty and a filled queue. Of course, such a situation cannot satisfy us.
One solution is to donate one element of the array and allow the queue to grow to a volume of one less than the maximum. So, if an array of 100 elements is declared as a queue, then the queue can contain up to 99 elements. Attempting to queue the 100th element will overflow. The insert subroutine can be written as follows:
if R = max (q)
then R = 1
else R = R + 1
endif
'overflow check
if R = F
then print "queue overflow"
stop
endif
q (r) = x
return
Check for overflow in the insert subroutine is performed after setting a new value for R, while checking for underflow in the remove subroutine is performed immediately after entering the subroutine before updating the F value.
From English DEQ - Double Ended Queue (Queue with two ends)
A special feature of decks is that elements can be written and read from two ends (Fig. 2.18).

Dec can also be viewed as two stacks connected by lower boundaries. Take an example illustrating the principle of building a deck. Consider the composition of the railway station. New cars to the composition can be added either to its end, or to the beginning. Similarly, in order to detach a car in the middle from the train, you must first detach all the cars either at the beginning or at the end of the train, disconnect the car you need and then attach them again.
Deck operations:
test questions
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.