Introduction Course work is performed by students of the specialty 22.04 in the fourth semester.
The Aim of the course work is to consolidate the foundations and deepening of knowledge in the field of structures and algorithms for data processing in computers.
The subject of coursework assignments given in these guidelines can be supplemented, expanded, linked to the solution of actual research tasks performed at the department.
1 Coursework Requirements
1.1 The topic of the course work is given to each student individually. In the collective work in which two or more students take part, the volume and nature of the work of each student are clearly defined. The task formulates the task, the method of its solution.
1.2 Coursework consists of an explanatory note, to which is attached a diskette with debugged programs (an explanatory note can be made in the form of a text file in Microsoft Word format).
1.3 The explanatory note should include:
- title page (Appendix B);
- task for course design (Appendix A);
- abstract (PP, the number of tables, figures, diagrams, application programs, a brief description and results of work);
- content:
a) formulation of the research problem;
b) a brief theory on the topic of the course work;
c) software implementation of the investigated algorithms;
d) the program with which the study was conducted;
e) the results of the study:
f) conclusions;
- list of references;
- signature, date.
1.4 The explanatory note should be issued on A4 sheets that have margins. All sheets should be stitched and numbered.
1.5 The study of algorithms for operations on data structures and methods of sorting and searching should be carried out with the following fixed quantities of elements in the structures: 10, 100, 1000, 10000.
1.6 Additional terms of coursework are issued by the supervisor.
2. Approximate list of coursework
1) Study Stacks.
2) Queue research.
3) The study of ring structures.
4) The study of semi-static structures.
5) The study of linear single and doubly linked lists.
6) Examination of binary search trees.
7) Research on inclusion sorting methods.
8) Exploring sorting methods of choice.
9) Research on exchange sorting methods.
10) Exploring sorting methods using trees.
11) Research on improved sorting methods.
12) The study of linear, index and binary searches.
13) The study of search optimization methods.
14) Research the search tasks on the tree.
3. Example of coursework
3.1 Problem Statement
Carry out a study of direct methods of sorting:
- direct selection method;
- direct insertion method;
- direct exchange method.
The study carried out using arrays of ordered and unordered numbers of 10,100,1000 and 10,000 items.
3.2 Brief Theory
When processing data, it is important to know both the information field of the data and its location in the machine.
There are internal and external sorting:
internal sorting - sorting in RAM;
external sorting - sorting in external memory.
Sorting is the arrangement of data in memory in a regular form by their keys. Regularity is considered as an increase (decrease) of the key value from the beginning to the end in the array.
If the sorted records occupy a large amount of memory, then their movement is expensive. In order to reduce them, the sorting is performed in the
table of key addresses , the permutation of pointers is performed, i.e. the array itself does not move. This is a
method to sort the address table. When sorting can meet the same keys. In this case, when sorting, it is desirable to arrange after sorting the same keys in the same order as in the source file. This is a
stable sort .
The sorting efficiency can be viewed from several criteria:
time spent on sorting;
the amount of RAM required for sorting;
time spent by a programmer to write a program.
Select the first criterion. You can count the number of comparisons when performing sorting or the number of movements.
Let H = 0.01n
2 + 10n be the number of comparisons. If n <1000, then the second term is greater; if n> 1000, then the first term is greater.
That is, for small n, the order of comparison will be equal to n
2 , for large n, the order of comparison will be n.
The order of comparison when sorting lies within
from 0 (n log n) to 0 (n
2 ); 0 (n) is an ideal case.
The following sorting methods are distinguished:
strict (direct) methods;
improved methods.
Strict methods:
1) direct inclusion method;
2) direct selection method;
3) direct exchange method.
The number of movements in these three methods is about the same.
3.2.1 Sort by direct inclusion Informal algorithm
for i = 2 to n
x = a (i)
find a place among a (1) ... a (i) to include x
next i
Pascal program:
for i: = 2 to n do
begin
x: = a [i];
a [0] = x;
for j: = i - 1 downto 1 do
if x <a [j]
then a [j + 1]: = a [j]
else a [j + 1]: = x;
end;
|
Algorithm efficiency: The number of comparisons in the worst case will be equal to
(n - 1) (n - 1).
3.2.2 Sorting by direct selection Consider the entire array row and choose an element smaller or larger than element a (i), determine its place in the array - k, and then swap element a (i) and element a (k).
Pascal program:
for i: = 1 to n - 1 do
begin
x: = a [i];
k: = i;
for j: = i + 1 to n do
if x> a [j] then
begin
k: = j;
x: = a [k];
end;
a [k]: = a [i];
a [i]: = x;
end; |
Algorithm efficiency: The number of comparisons M =
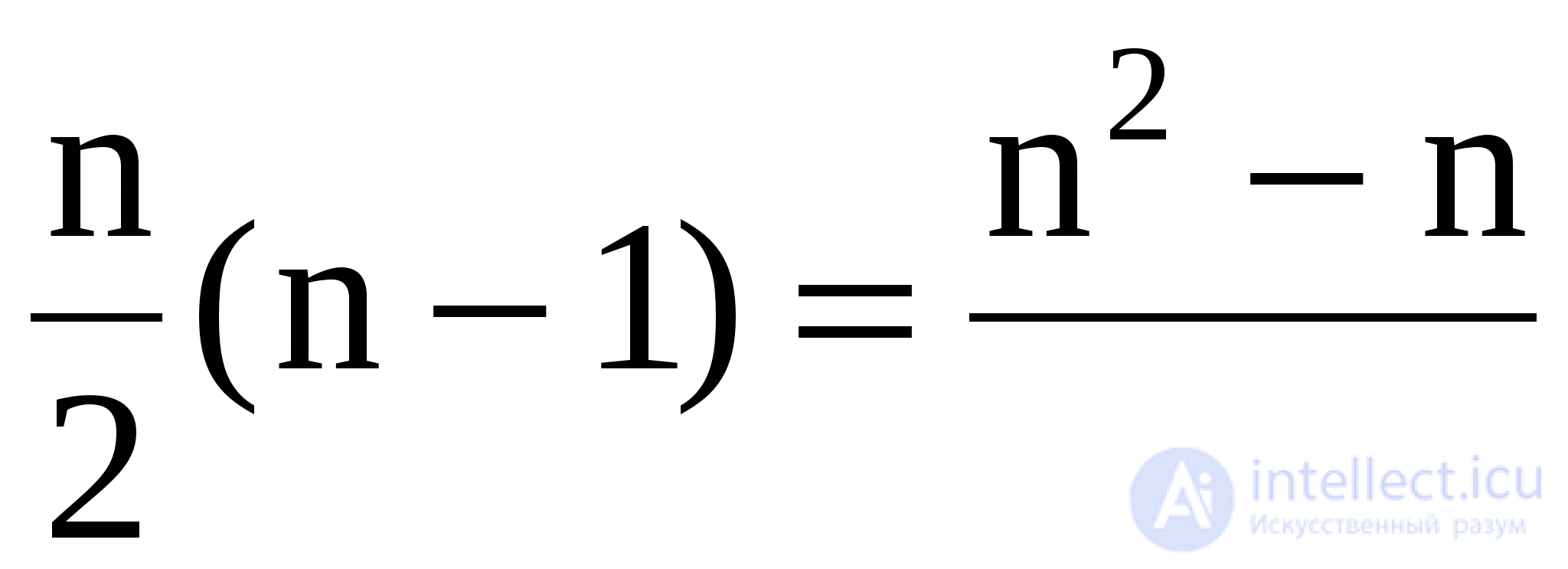
.
The number of displacements C
min = 3 (n - 1), C
max = 3 (n - 1)
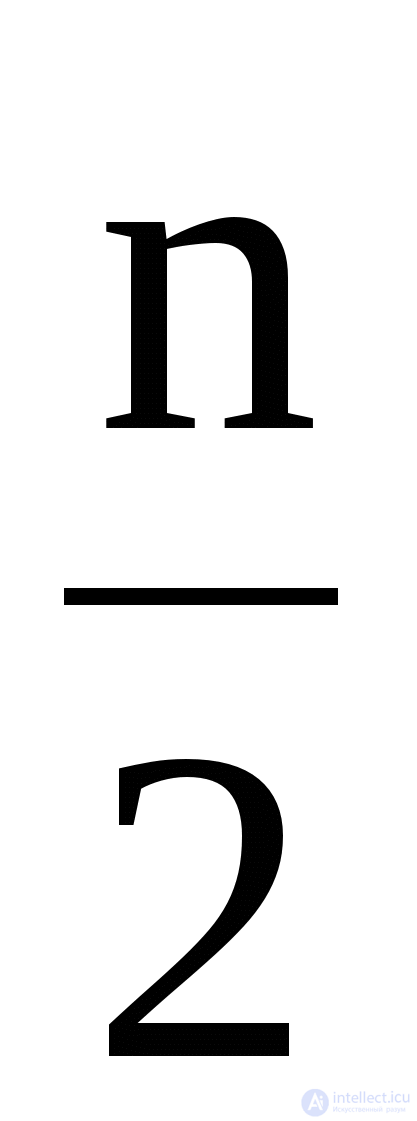
(order n
2 ).
In the worst case, sorting by direct choice gives the order of n
2 , as for the number of comparisons, and for the number of displacements.
3.2.3 Sort using direct exchange (bubble) Idea: n - 1 times pass an array from the bottom up. In this case, the keys are compared in pairs. If the lower key in a pair is less than the upper key, then they are swapped.
Pascal program:
for i: = 2 to n do
for j: = n downto i do
if a [j - 1]> a [j] then
begin
x: = a [j - 1];
a [j - 1]: = a [j];
a [j]: = x;
end;
|
In our case, it turned out one pass “idle”. In order not to rearrange the elements again, you can enter a flag.
The improvement of the bubble method is shaker sorting, where after each pass they change direction within the cycle.
Algorithm efficiency: number of comparisons M =
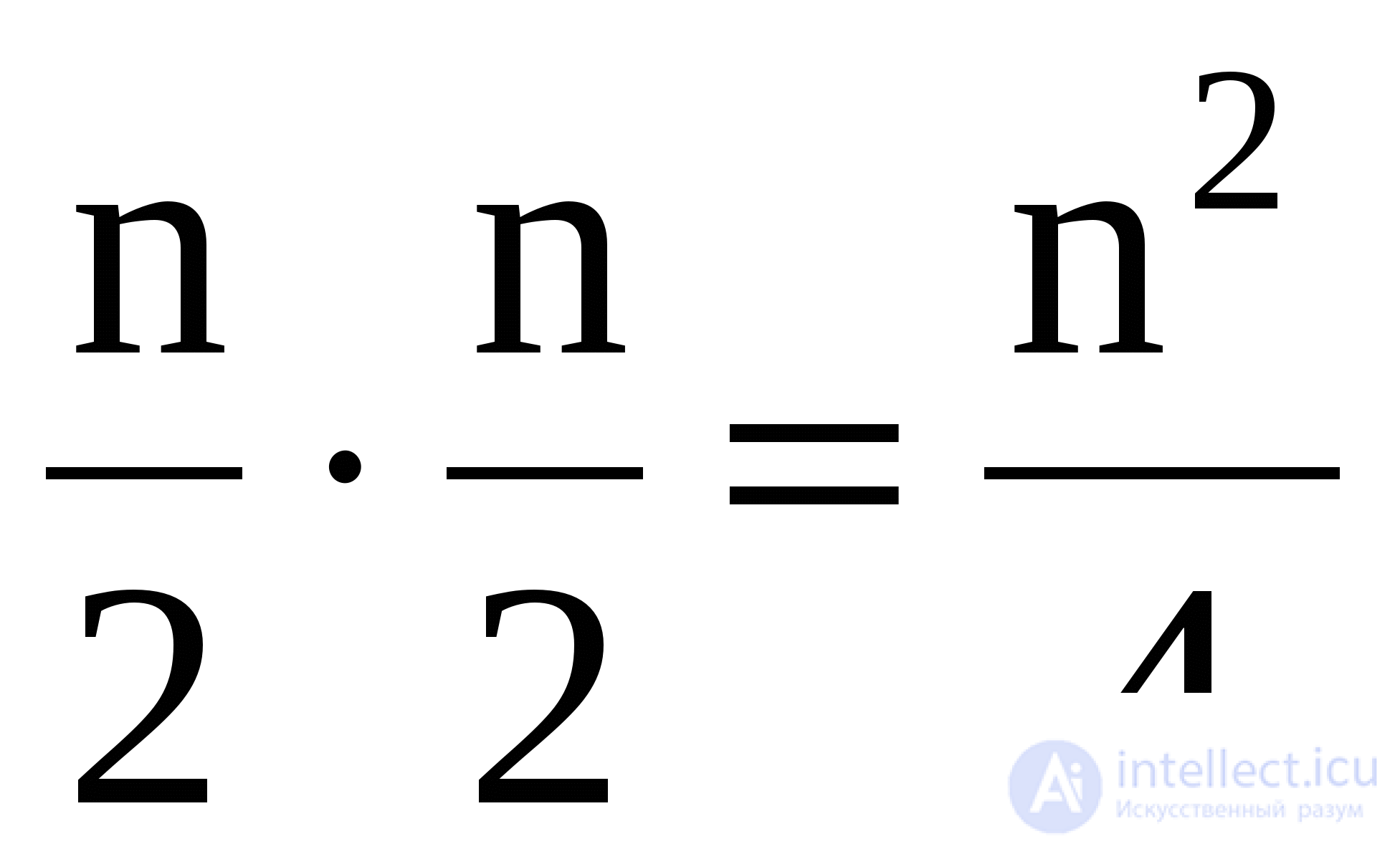
,
number of movements C
max = 3
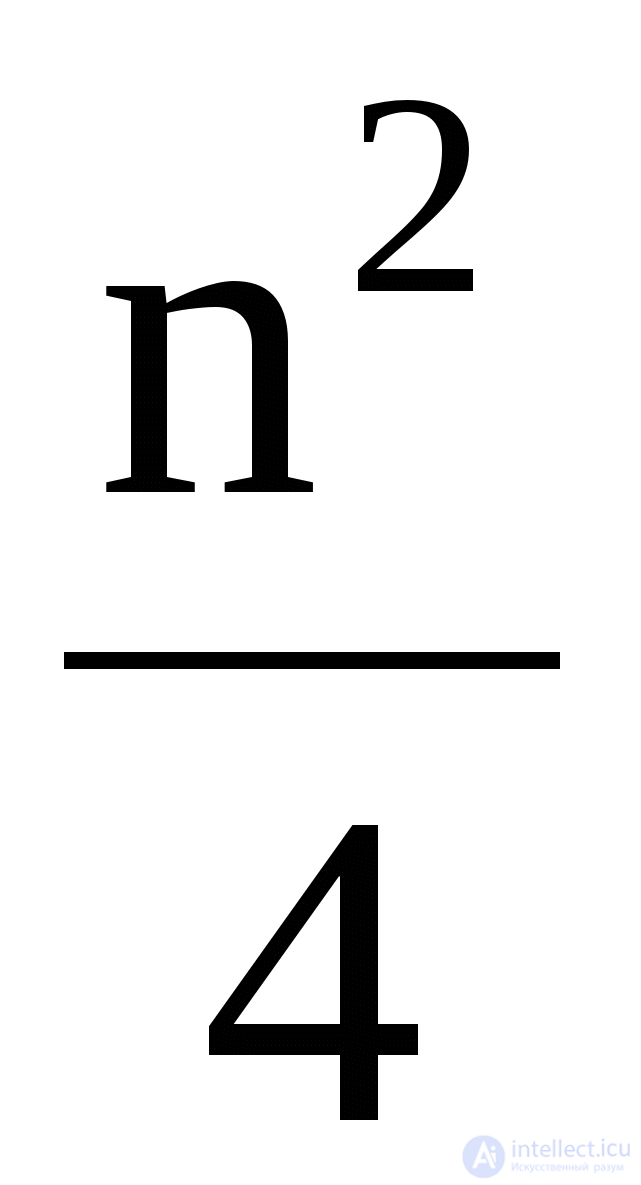
.
3.3 Research Method
This course work is to study the direct methods of sorting:
- direct selection method;
- direct inclusion method;
- direct exchange method.
The study is as follows:
they take three arrays with the same number of elements, but one of them is ordered in ascending order, the second is in descending order, and the third is random. The data of the arrays is sorted and the number of elements displacements is compared when the first, second and third arrays are sorted, and the number of comparisons is compared.
The above method is applied to arrays consisting of 10, 100, 1000 and 10000 ordered and unordered elements for all sorting methods.
3.4 study results
Sorting 10 items: |
- ordered by ascending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
45 |
45 |
45 |
displacements |
eleven |
33 |
33 |
- unordered (random) |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
45 |
45 |
45 |
displacements |
27 |
27 |
27 |
- ordered by descending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
45 |
45 |
45 |
displacements |
0 |
0 |
0 |
Sorting 100 items: |
- ordered by ascending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
4950 |
4950 |
4950 |
displacements |
2643 |
4862 |
4862 |
- unordered (random) |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
4950 |
4950 |
4950 |
displacements |
2558 |
2558 |
2558 |
- ordered by descending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
4950 |
4950 |
4950 |
displacements |
0 |
0 |
0 |
Sorting 1000 items: |
- ordered by ascending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
499,500 |
499,500 |
499,500 |
displacements |
241901 |
498442 |
498442 |
- unordered (random) |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
499,500 |
499,500 |
499,500 |
displacements |
244009 |
250366 |
250366 |
- ordered by descending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
499,500 |
499,500 |
499,500 |
displacements |
0 |
0 |
0 |
Sorting 10,000 items: |
- ordered by ascending |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
49995000 |
49995000 |
49995000 |
displacements |
25003189 |
49984768 |
49984768 |
- unordered (random) |
method |
direct selection |
direct insertion |
direct exchange |
comparisons |
49995000 |
49995000 |
49995000 |
displacements |
18392665 |
24986578 |
24986578 |
- ordered by descending |
method |
direct selection |
direct bet |
direct exchange |
comparisons |
49995000 |
49995000 |
49995000 |
displacements |
0 |
0 |
0 |
3.5 Test Case
The task: A list containing the names of the students and their corresponding rating points is given. It is necessary to sort this list by descending rating points.
Sort by direct inclusion:
Before sorting |
After sorting |
Arkady |
nineteen |
Arthur |
20 |
Before sorting |
After sorting |
Murat |
17 |
Arkady |
nineteen |
Ruslan |
9 |
Alexander |
18 |
Arthur |
20 |
Vladimir |
18 |
Eugene |
7 |
Murat |
17 |
Michael |
15 |
Kazbek |
sixteen |
Alexander |
18 |
Michael |
15 |
Vitali |
14 |
Boris |
15 |
Sidor |
eight |
Denis |
14 |
Vladimir |
18 |
Vitali |
14 |
Alexey |
6 |
Vasiliy |
13 |
Kazbek |
sixteen |
Peter |
ten |
Marat |
five |
Ruslan |
9 |
Boris |
15 |
Ivan |
eight |
Gennady |
2 |
Sidor |
eight |
Denis |
14 |
Eugene |
7 |
Vasiliy |
13 |
Alexey |
6 |
Sidor |
3 |
Marat |
five |
Peter |
ten |
Sidor |
3 |
Ivan |
eight |
Gennady |
2 |
3.6 Conclusions
According to the results of the research, it can be argued that the best of the direct sorting methods is the direct selection method, since it gives the least amount of comparisons and movements, regardless of the number of elements being sorted and their relative position in the array.
3.7 Description of the procedures used in the program
UPOR |
the procedure generates an ascending array of numbers |
NOTUPOR |
the procedure generates an unordered (random) array of numbers |
PR_CHOOSE |
procedure performs sorting by direct selection |
PR_INS |
the procedure performs the direct insert sorting |
PR_OBM |
procedure performs the direct exchange sorting |
MAKE |
the procedure carries out research of direct methods of sorting |
EXAMPLE |
the procedure performs a test case (live sorting) |
Text of the program {$ M 65000.65000.65000}
{Memory allocation is carried out in order to make it possible to study an array containing 10,000 elements.
************************************************** *********
This program is a course work on discipline.
'Structures and Data Processing Algorithms'
on the topic 'Direct sorting methods'
In work methods are investigated:
- direct selection;
- direct exchange;
- direct insertion.
For research, arrays of 10,100,100,10000 elements are used.
************************************************** ********}
{using modules for displaying}
uses crt, crtext, dcrt; ******************************************* ********}
{** procedure that generates an ordered array of numbers **}
{************************************************* ********}
procedure upor (a: array of integer; var a1: array of integer);
var
{i - counter in cycles}
i: integer;
begin
{the first element takes the value 1}
a [0]: = 1;
for i: = 1 to high (a) do
begin
{each subsequent element takes the value
equal to the value of the previous element + random number}
a [i]: = a [i-1] + random (2);
end;
for i: = 0 to high (a) do
a1 [i]: = a [i];
end;
{************************************************* ********}
{** procedure generating an unordered (random) array of numbers **}
{************************************************* ********}
procedure notupor (a: array of integer; var a1: array of integer);
var
{i - counter in cycles}
i: integer;
begin
for i: = 0 to high (a) do
begin {array element takes a random value from the range 0 <= a [i] <9999}
a [i]: = random (9999);
end;
for i: = 0 to high (a) do
a1 [i]: = a [i];
end;
{************************************************* ********}
{***** procedure that performs sorting by direct selection ***}
{************************************************* ********}
procedure pr_choose (a: array of integer; var a1: array of integer; var k, k1: longint);
var
{i, j - counters in cycles}
i, j: integer;
{x - variable for exchanging between a [i] and a [j]}
x: integer;
begin
{k1 - variable to count the number of comparisons
k - variable to count the number of displacements}
k: = 0; k1: = 0;
{high (a) - a function that returns the number of the last element of the array}
for i: = 0 to high (a) - 1 do
begin
for j: = i + 1 to high (a) do
begin
k1: = k1 + 1;
if a [i] <a [j] then
begin
k: = k + 1;
{interchanging the ith with the jth element using the variable x}
x: = a [i];
a [i]: = a [j];
a [j]: = x;
end;
end;
end;
for i: = 0 to high (a) do
a1 [i]: = a [i];
end;
{************************************************* *********
***** Direct Sorting Procedure *
*************** exchange (bubble method) *********************
************************************************** ********}
procedure pr_obm (a: array of integer; var a1: array of integer; var k, k1: longint);
var
{i, j - counters in cycles}
i, j: integer;
{x - variable to exchange between a [j-1] and a [j]}
x: integer;
begin
{k1 - variable to count the number of comparisons
k - variable to count the number of displacements}
k: = 0; k1: = 0;
for i: = 1 to high (a) do
begin
for j: = high (a) downto i do
begin
k1: = k1 + 1;
if a [j - 1] <a [j] then
begin
k: = k + 1;
{exchange the contents of the elements of the array a [j-1] and a [j]
using the variable x}
x: = a [j - 1];
a [j - 1]: = a [j];
a [j]: = x;
end;
end;
end;
for i: = 1 to high (a) do
a1 [i]: = a [i];
end;
{************************************************* ********}
{*** procedure that performs the sorting method by direct inclusion **}
{************************************************* ********}
procedure pr_ins (a: array of integer; var a1: array of integer; var k, k1: longint);
var
{i, j - counters in cycles}
i, j: integer;
{x - variable for exchanging between a [i] and a [j]}
x: integer;
begin
{k1 - variable to count the number of comparisons
k - variable to count the number of displacements}
k: = 0; k1: = 0;
for i: = 1 to high (a) do
begin
x: = a [i];
for j: = i - 1 downto 0 do
begin
k1: = k1 + 1;
if x> a [j] then
begin
k: = k + 1;
{exchange the contents of the elements of the array a [j + 1] and a [j]
using the variable x}
a [j + 1]: = a [j];
a [j]: = x;
end;
end;
end;
for i: = 0 to high (a) do
a1 [i]: = a [i];
end;
{************************************************* *********
procedure that investigates sorting methods for
*********** a given array of numbers ***********************
************************************************** ********}
procedure make (x1, n: integer; a, a1: array of integer; k: byte);
var
{number of permutations}
kol_pr_ins, kol_pr_obm, kol_pr_choose: longint;
{number of comparisons}
kol_sr_ins, kol_sr_obm, kol_sr_choose: longint;
s: string;
begin
case k of
1: s: = 'sorted in ascending order';
2: s: = 'unordered (random)';
3: s: = 'ordered descending';
end;
{-------- direct inclusion method --------}
pr_ins (a, a1, kol_pr_ins, kol_sr_ins);
{-------- direct exchange method (bubble method) --------}
pr_obm (a, a1, kol_pr_obm, kol_sr_obm);
{--------- direct selection method ----------}
pr_choose (a, a1, kol_pr_choose, kol_sr_choose);
{** output research result **}
{output table header}
gotoxy (3, x1); textcolor (cyan); textbackground (1);
writeln ('For', high (a) +1, '', s, 'elements:');
gotoxy (3, x1 + 1); textcolor (lightgreen); textbackground (1);
writeln ('Methods: direct inclusion direct exchange direct selection');
{output of the data obtained during the study}
gotoxy (3, x1 + 2); textcolor (white); write ('overwrite');
gotoxy (17, wherey); write (kol_pr_ins);
gotoxy (37, wherey); write (kol_pr_obm);
gotoxy (58, wherey); writeln (kol_pr_choose);
gotoxy (3, x1 + 3); write ('compare.');
gotoxy (17, wherey); write (kol_sr_ins);
gotoxy (37, wherey); write (kol_sr_obm);
gotoxy (58, wherey); writeln (kol_sr_choose);
str (high (a) + 1, s); box (1,19,80,24,1,15, double, s + 'elements');
gotoxy (4,20); write ('Sort', s, 'items descending');
gotoxy (4,21); write ('Sorted', s, 'ordered (by ascending) elements');
gotoxy (4.22); write ('Sorted', s, 'unordered (random) elements');
textbackground (lightgray);
textcolor (red); gotoxy (3.25); write ('Esc - main menu');
end;
{*********************************************
Live Sorting Example
An array of entries is given containing:
-name of the student;
-kol points (rating).
You must sort the array by
a decrease in the number of points from the student.
**********************************************}
procedure example;
type
{rec is a record containing:
name - the name of the student;
num - number of points (rating).}
rec = record
name: string;
num: byte;
end;
var
{mas - array of rec records}
mas: array [1..20] of rec;
{counters in cycles}
i, j: integer;
x: rec;
{variables for counting the number of comparisons and movements
during sorting}
k_sr, k_p: integer;
key: char;
begin
{variables for counting the number of comparisons and movements
during sorting}
k_sr: = 0; k_p: = 0;
randomize;
{This array containing the names of the students}
mas [1] .name: = 'Ivan'; mas [2] .name: = 'Peter'; mas [3] .name: = 'Sydor';;
mas [4] .name: = 'Basil'; mas [5] .name: = 'Denis'; mas [6] .name: = 'Gennady';;
mas [7] .name: = 'Boris'; mas [8] .name: = 'Marat'; mas [9] .name: = 'Kazbek';
mas [10] .name: = 'Aleksey'; mas [11] .name: = 'Vladimir'; mas [12] .name: = 'Sydor';;
mas [13] .name: = 'Vitaly'; mas [14] .name: = 'Alexander'; mas [15] .name: = 'Michael';
mas [16] .name: = 'Eugene'; mas [17] .name: = 'Arthur'; mas [18] .name: = 'Ruslan';;
mas [19] .name: = 'Murat'; mas [20] .name: = 'Arkady';
{setting the number of points for a student at random}
for i: = 1 to 20 do
mas [i] .num: = random (19) +1;
{conclusion of explanations}
getshadow;
textbackground (lightgray);
textcolor (red); gotoxy (15,1); write ('Example of sorting in descending order by direct inclusion');
textbackground (lightgray);
textcolor (red); gotoxy (3.25); write ('Esc - main menu');
textcolor (red); gotoxy (65.25); write ('F1 - task');
box (58,0,80,25,1,15, double, 'Statistics');
textcolor (lightmagenta);
gotoxy (59.3); write ('Sort method');
gotoxy (61,4); write ('live.');
textcolor (white); gotoxy (59.5); write ('---------------------');
box (31,0,57,25,1,15, double, 'After sorting');
textcolor (lightmagenta); gotoxy (32.3); write ('n name score');
box (1,0,30,25,1,15, double, 'Before sorting');
textcolor (lightmagenta); gotoxy (3.3); write ('n name score');
{output to the screen of the original array}
for i: = 1 to 20 do
begin
textcolor (lightcyan); gotoxy (3, i + 3); write (i);
textcolor (yellow); gotoxy (7, i + 3); write (mas [i] .name);
textcolor (lightred); gotoxy (25, i + 3); writeln (mas [i] .num);
end;
{sort by descending number of points}
for i: = 2 to 20 do
begin
x: = mas [i];
for j: = i - 1 downto 1 do
begin
{k_sr - number of comparisons}
k_sr: = k_sr + 1;
if x.num> mas [j] .num then
begin
{k_p - the number of displacements}
k_p: = k_p + 1;
{sharing the contents of the elements of the mas [j + 1] and mas [j] array
using the variable x}
mas [j + 1]: = mas [j];
mas [j]: = x;
end;
end;
end;
{display of sorted array}
for i: = 1 to 20 do
begin
textcolor (lightcyan); gotoxy (33, i + 3); write (i);
textcolor (yellow); gotoxy (37, i + 3); write (mas [i] .name);
textcolor (lightred); gotoxy (52, i + 3); writeln (mas [i] .num);
end;
{display the number of comparisons and permutations
in an array, implemented during sorting}
textcolor (lightgreen); gotoxy (61.6); write ('Comparisons:');
textcolor (lightgray); gotoxy (75.6); write (k_sr);
textcolor (lightgreen); gotoxy (61.8); write ('Permutations:');
textcolor (lightgray); gotoxy (75.8); write (k_p);
repeat
key: = ''; if keypressed then key: = readkey;
case key of
{# 59 - F1 key code}
# 59: begin
{output of task window for test case}
{putshadow + box - output window with shadow}
putshadow (15,7,65,15); box (15,7,65,15, lightgray, 0, double, 'Task');
textcolor (red);
gotoxy (21.9); write ('There is a list containing the names of the students');
gotoxy (21,10); write ('and their rating points. Necessary from-');
gotoxy (21.11); write ('sort the list in descending order');
gotoxy (21,12); write ('rating points.');
textcolor (yellow); gotoxy (50,15); write ('Enter - cancel');
end;
{# 13 - Enter key code}
# 13: getshadow;
end;
{# 27 - Esc key code}
until key = # 27;
end;
{************************************************* *********
************************ Main program ***************
************************************************** ********}
const
{array of strings - main menu items}
menu: array [1..7] of string = ('Example sorting', 'Research (10 items)',
'Research (100 el-com)',
'Research (1000 email)',
'Research (10,000 email)',
' About the program '
,' Output ');
var
{arrays of numbers used for research}
a, a1: array [0..9] of integer; {10 - numbers}
b, b1: array [0..99] of integer; {100 - numbers}
c, c1: array [0..999] of integer; {1000 - numbers}
d, d1: array [0..9999] of integer; {10,000 - numbers}
f: byte; {indicator of which array
enters the procedure for
descending:
1 - unordered (case
tea);
2 - ordered by opportunity
sprawl;
3 - ordered by decrease
to
k: char;
item: byte;
begin
clrscr; cursoroff; {cursor blanking}
repeat
textbackground (0); clrscr;
{fill - a procedure that fills a specified area of the screen with specified characters of a given color}
fill (lightgray, 1,1,2,80,25, '');
{menuv - procedure that displays the vertical menu}
menuv (25,10, menu, lightgray, black, red, lightgreen, yellow, 'Sort', item, double);
{item - a variable containing the number of the selected menu item}
case item of
1: example;
2: begin
{getshadow - procedure that removes the shadow from the menu}
getshadow;
{** 10 elements in ascending order are examined **}
{box - procedure that displays the window}
box (1,0,80,18,1,15, double, '10 elements');
{call upor, generating an ascending order
array of numbers}
upor (a, a);
{call to the make procedure that investigates sorting methods}
make (3,10, a, a1,1);
{** 10 unordered (random) elements are investigated **}
{call the notupor procedure that generates an unordered (random) array of numbers}
notupor (a, a);
{call to the make procedure that investigates sorting methods}
make (8.10, a, a1,2);
{** 10 descending ordered elements descending **}
{call to the make procedure that investigates sorting methods}
make (13,10, a1, a1,3);
{waiting for Esc key press}
repeat
k: = readkey;
until k = # 27; end;
3: begin {getshadow - a procedure that removes the shadow from the menu} getshadow; {box - a procedure that displays a window} box (1,0,80,18,1,15, double, '100 elements'); {100 ordered ascending elements are examined } upor (b, b); make (3,100, b, b1,1); {100 unordered (random) elements are investigated } notupor (b, b); make (8,100, b, b1,2); {100 ordered elements descending are examined} make (13,100, b1, b1,3); repeat k: = readkey; until k = # 27; end;
4: begin {getshadow - a procedure that removes the shadow from the menu} getshadow; box (1,0,80,18,1,15, double, '1000 elements'); {1000 ordered ascending elements are examined } upor (c, c); make (3,1000, c, c1,1); {1000 unordered (random) elements are investigated } notupor (c, c); make (8,1000, c, c1,2); {1000 ordered by descending elements are examined} make (13,1000, c1, c, 3); repeat
k: = readkey; until k = # 27; end;
5: begin getshadow; box (1,0.80,18,1,15, double, '10,000 items'); {10,000 elements in ascending order are examined} upor (d, d); make (3.10000, d, d1,1); {10,000 unordered (random) elements are investigated } notupor (d, d); make (8,10000, d, d1,2); {10,000 ordered elements descending are investigated} make (13,10000, d1, d, 3); repeat
k: = readkey; until k = # 27; end;
6: begin {getshadow - a procedure that removes the shadow from the menu} getshadow; {enter the window with the topic of the course work} box (10,5,70,15, lightgray, 0, double, 'About the program'); putshadow (10,5,70,15); textcolor (brown); gotoxy (12,7); write ('This program is a term paper on the discipline'); gotoxy (21,8); write ('"Algorithms and data processing structures"'); gotoxy (30,9); write ('Theme of the course work:'); gotoxy (18,10); write ('"Investigating direct sorting methods"'); gotoxy (17,11); write ('Course work was completed by students of group 95-OA-21'); textcolor (red); gotoxy (3.25); write ('Esc - main menu'); repeat
k: = readkey; until k = # 27; end;
end;
until item = 7; end.
{********************* end of program ********************} 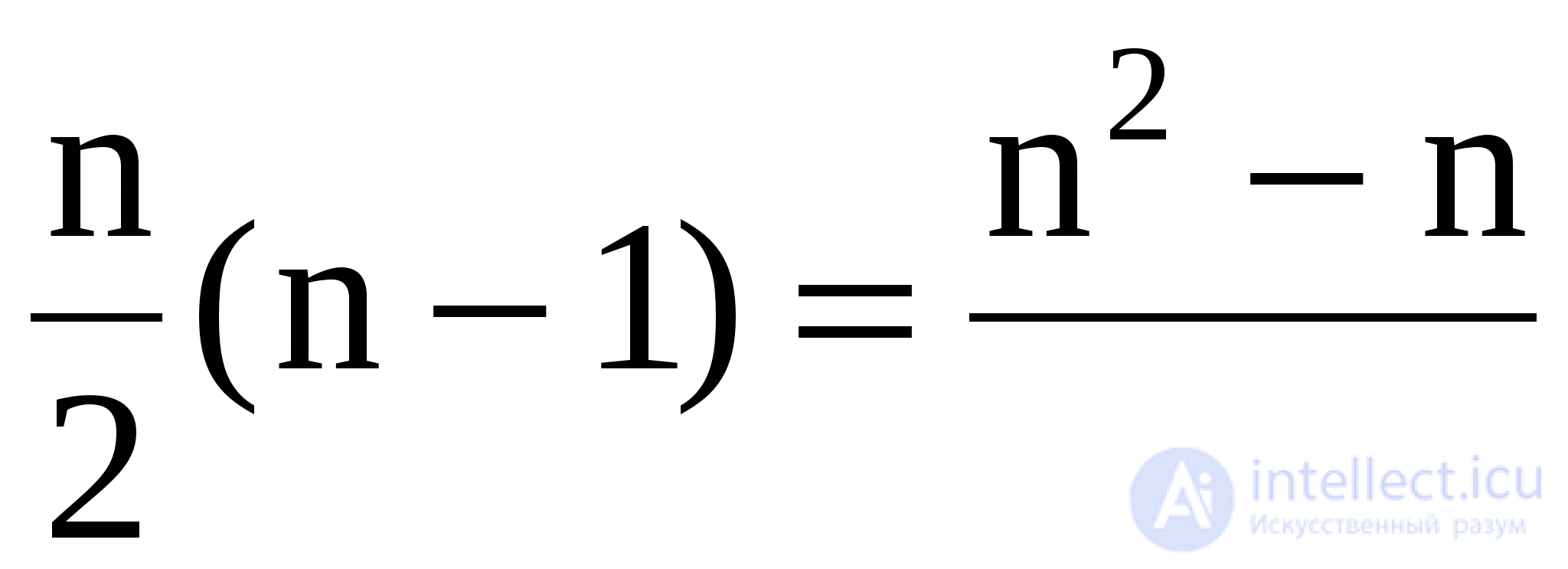 .
. 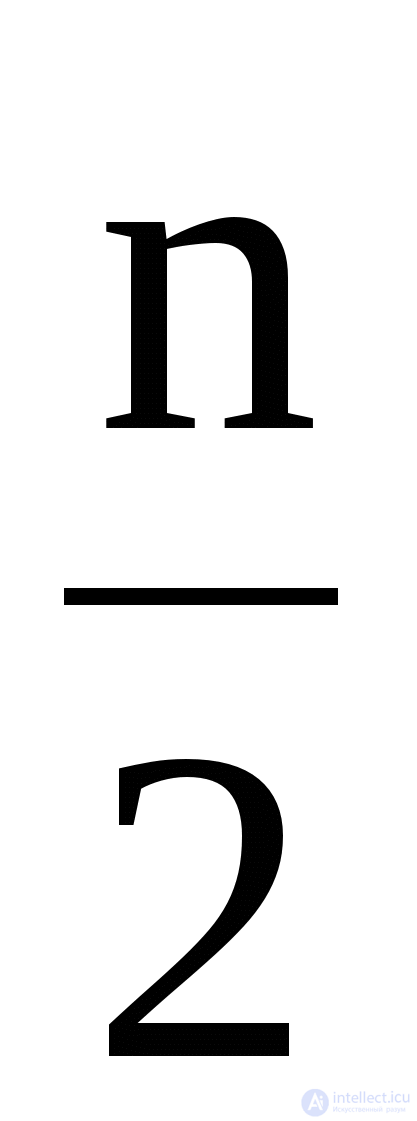
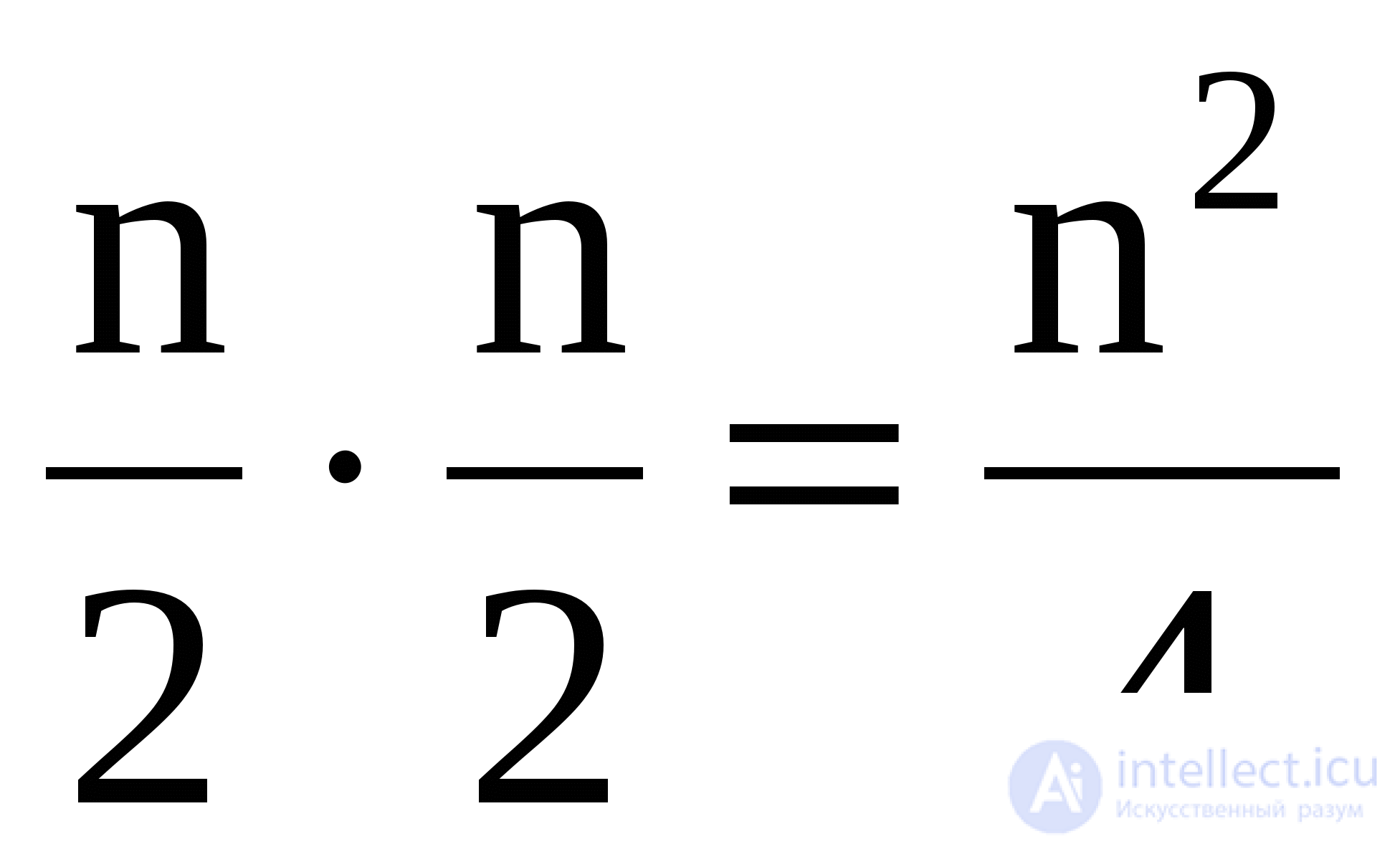 ,
, 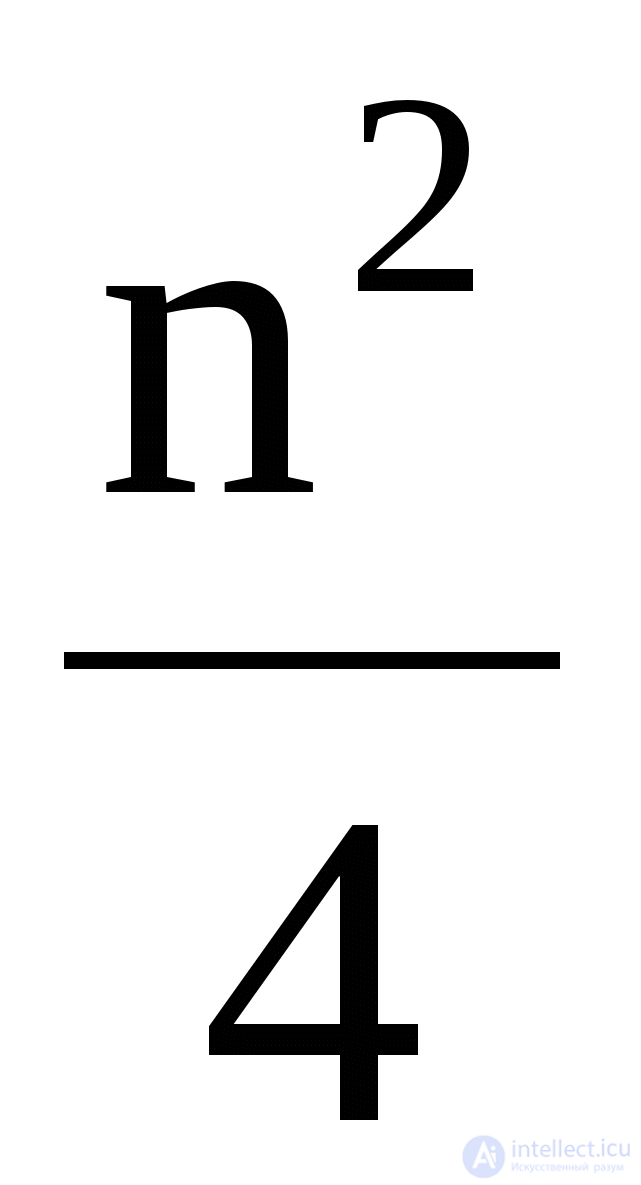 .
.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.