Counts. Representation of graphs in computer memory

a) Introduction

To begin, let us figure out what the graph is and what they are.

A graph is a set of V vertices and a set of E unordered and ordered pairs of vertices. Simply put, a graph is a set of points (vertices) and paths connecting them (arcs or edges). Count can be oriented and non-oriented. In an oriented graph, paths (arcs) have a direction, but in an undirected direction they do not. Paths in an undirected graph are called edges.

Such a graph is called weighted, for each edge (arc) of which a certain function is defined. And this function is called weight.

Consider an example of a directed weighted graph:

Example of a weighted oriented graph

In the figure, dots mark the vertices of the graph, the arrows indicate the arcs, the black numbers the numbers of the vertices of the graph, and the red numbers the weights of the arcs. The weight of the arc can also be represented as a cost. Those. for example: a graph is given, you need to walk from vertex i to vertex j, paying the minimum amount of money / spending the least amount of time. Suppose that in our graph, which is shown in the figure, we need to go from vertex 5 to vertex 2, and the weight of the arcs is the cost of passage along this edge. In this example, it is obvious that it is more profitable to go through the top 1 and only then come to the top 2, so we will pay only 4 units of money, otherwise, if we go directly, we will pay as many as 7 units.

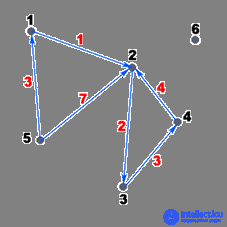
Picture 1.

In the picture, everything looks beautiful, all problems seem to be solved easily ... But if the graph is really big, for example, for 1000 vertices? Yes, such a graph on a piece of paper to draw is very long and unpleasant ... Let it be better that all this makes a computer for us!

The problem of proper storage of the graph in the memory of a computer is really relevant today.

b). Graph Submission Requirements

There are various ways to represent graphs in computer memory, which ry differ in the amount of memory occupied and the speed of execution of oneractions on graphs. The presentation is selected based on the needs of a specific task. The following are four of the most frequently used representations with an indication of the characteristics of n (p, q ) —the amount of memory for each representation. Here p is the number of vertices, and q is the number of edges.

NOTE These representations are suitable for graphs and digraphs, and after some modification also for pseudographs, multigraphs, and hypergraphs.

Representations are illustrated with specific examples of the graph G and the digraph D of the diagrams of which are shown in Fig. 2

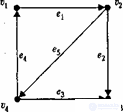
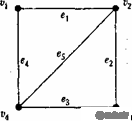
Figure 2. Graphs of the graph (left) and digraph (right) used as examples

c) adjacency matrix

Representation of a graph using a square Boolean matrix

M : array [l..p, l..p] of 0..1,

reflective adjacency of vertices, is called an adjacency matrix, where

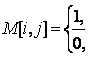if the vertex v _i is adjacent to the vertex v _j

if vertices v _i and v _{j are} not adjacent.

For the adjacency matrix, n (p, q) = O (p ² )

Example

In addition to the large amount of required memory and slow work on sparse graphs (graphs that have E << V2), the adjacency matrix has another important drawback. Sometimes in tasks it is necessary to output not the numbers of the vertices, but the numbers of the arcs (edges) on the input. Store these numbers adjacency matrix "can not." It is necessary to implement the restoration of the arc number (edge) somehow differently, and this is completely inconvenient.

We present calculations of the time complexity of storing a graph with an adjacency matrix:

Operation Time Difficulty

Verification of adjacency of vertices x and y О (1)

Enumeration of all vertices adjacent to x О (V)

Determining the weight of the edge (x, y) O (1)

Enumeration of all edges (x, y) О (V ² )

Enumeration of edges incident to vertex x Edge numbers are not stored

Enumeration of vertices incident to the edge s Edge numbers are not stored

Determining the weight of the vertex x О (1)

d) Incident Matrix

Representation of a graph using the matrix H: array [l..p, l..q] of 0..1 (for digraphs H : array [l..p, l..q] of -1..1), reflecting the incidence of vertices and edges is called an incident matrix , where for an undirected graph

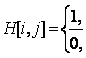
if the vertex v _{i is} incident to the edge e _j

otherwise,

and for a directed graph

if the vertex v _{i is} incident to the edge e _j and is its end

if the vertex v _i and the edge e _{j are} not incidient,

if the vertex v _{i is} incident to the edge e _j and is its beginning.

For the incidence matrix, n (p, q) = O (pq).

Example

The spatial complexity of this method is O (N * M). Temporary difficulties are tabulated.

Operation Time Difficulty

Check adjacency vertices x and y T (M * N)

Enumerate all vertices adjacent to x T (M * N)

Determining the weight of the edge (x, y) T (M * N)

Vertex weight determination x Vertex weight is not stored

Enumeration of all edges (x, y) T (M)

Enumeration of edges incident to a vertex x T (M)

Enumeration of vertices incident to the edge s T (N)

The incidence matrix is ​​best suited for the operation “enumeration of edges incident to vertex x”.

e) Adjacency Lists

Representation of a graph using a list structure reflecting the vertices adjacency and consisting of an array of pointers Γ : array [l..p] N to lists of adjacent vertices (an element of the list is represented by the structure N : record v: l..p; n: N endrecord), is called adjacency list. In the case of representing undirected graphs as adjacency lists, n (p, q) = O (p + 2q), and in the case of oriented graphs, n (p, q) = O (p + q).

Example

The adjacency lists for the graph G and the digraph D are presented in Fig. 3

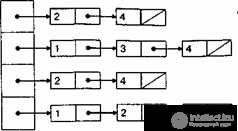
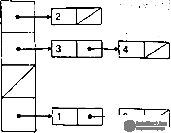
Figure 3 . Adjacency lists for graph G (left) and digraph D (right)

We present the calculations of the time complexity of storing a graph by lists of adjacent vertices:

Operation Time Difficulty

Verifying the adjacency of vertices x and y О (E)

Enumeration of all vertices adjacent to x О (E)

Determining the weight of the edge (x, y) O (E)

Enumeration of all edges (x, y) О (E)

Search for the i-th arc O (1)

Times for all operations, like, the same as the list of edges. However, most of them are really much smaller. For example, checking the adjacency of vertices x and y and listing all vertices adjacent to x in the list of edges is guaranteed to perform O (E) operations, since we definitely need to run through the entire list, and in the adjacency list we run only along the vertices adjacent to x.

In addition, we save a tremendous amount of memory.

e) List of arcs (array of arcs)

The next type of graph storage in computer memory is a list of arcs. Most often it is a two-dimensional array of size 3 * E, in the first line of which information is stored, from which vertex the arc starts, in the second - which one ends, and in the third line - the weight of the arc. Again, let's look at an example

1 2 3 4 5 6

1 1 2 3 4 5 5

2 2 3 4 2 1 2

3 1 2 3 4 3 7

We clearly see that almost the entire table is filled with the "necessary" values, not zeros. This is already good, it means that memory is saved.

Representation of a graph using an array of structures E : array [1 .. p ] of record b , e : 1 .. p endrecord , reflecting a list of pairs of adjacent vertices, is called an array of edges (or, for digraphs, an array of arcs ). For an array of edges (or arcs), n ( p , q ) = O (2 q ).

Example

The representation using an array of edges (arcs) is shown in the following table (for the graph G on the left, and for the digraph D on the right).

b	e	b	e
one	2	one	2
one	four	2	3
2	3	2	four
2	four	four	one
3	four	four	s

Let us calculate the time complexity of storing a graph with a list of arcs:

Operation Time Difficulty

Verifying the adjacency of vertices x and y О (E)

Enumeration of all vertices adjacent to x О (E)

Determining the weight of the edge (x, y) O (E)

Enumeration of all edges (x, y) О (E)

Search for the i-th arc O (1)

As you can see, this method, in contrast to the adjacency matrix, stores information about the arc number. It is also clear that this method is beneficial for us, if more often we need to learn something (weight, tops of beginning or end) about the i-th arc. However, such tasks in practical programming are quite rare.

If in the previous views we replaced one edge with two arcs, then the list of arcs can store either arcs or edges (depending on the implementation). It is quite convenient and may require 2 times less memory.

g . Description of Berg

In order to speed up the work of the adjacency matrix on sparse graphs, you can use another type of graph storage - the description of Berg. For each vertex, a list of adjacent vertices is stored. Most often, a two-dimensional array of the size V in a square is used for this, in row u of which the numbers of vertices adjacent to u are stored. The zero element of the string u fits the number of vertices stored in this string. Now we will try to present our graph using the description of Berge using an example:

0 1 2 3 4 5 6

1 1 2 0 0 0 0 0

2 1 3 0 0 0 0 0

3 1 4 0 0 0 0 0

4 1 2 0 0 0 0 0

5 2 1 2 0 0 0 0

6 0 0 0 0 0 0

The zero column stores row lengths. However, the weight of the arcs is not stored at all, and if it is stored separately, then you need to start another array of size V in the square ...

Temporary difficulties are summarized in the table:

Operation Time Difficulty

Verifying the adjacency of vertices x and y О (V)

Enumeration of all vertices adjacent to x О (V)

Determining the weight of the edge (x, y) Weight is not stored

Enumeration of all edges (x, y) O (E)

h) Conclusion

to find a universal way of storing a graph in the computer's memory, which would store as much information as possible about the graph, work with any graphs and work a quick simple task, there is no universal way. For various tasks and graphs, various representations are optimal. Of course, the most powerful and versatile way to store is the adjacency list. it is often faster and still requires not so much memory. However, if the number of arcs approaches the square of the number of vertices, then there is no better way to find an adjacency matrix, since then the speed and amount of memory even the adjacency list approaches the adjacency matrix, if it does not require more ... Of course, you can write an adjacency list, but it is written longer than the adjacency matrix, and working with the adjacency matrix is ​​much easier.