Binary search tree

Sample binary search tree

A binary search tree (born binary search tree , BST) is a binary tree for which the following additional conditions are met ( properties of the search tree ):

• Both subtrees — left and right — are binary search trees.
• All nodes of the left subtree of an arbitrary node X have data key values less than the data key value of the node X itself.
• At the same time, the data key values ​​of all nodes of the right subtree (of the same node X) are greater than the value of the data key of node X.

Obviously, the data in each node must have keys that have a smaller comparison operation.

Typically, the information representing each node is a record, not a single data field. However, this concerns the implementation, not the nature of the binary search tree.

For the purposes of implementation, a binary search tree can be defined as:

• A binary tree consists of nodes (vertices) - records of the form (data, left, right), where data is some data attached to a node, left and right are references to nodes that are children of this node are left and right sons, respectively. To optimize the algorithms, specific implementations also imply the definition of the parent field in each node (except the root) - references to the parent element.
• Data (data) has a key (key) on which the comparison operation "less" is defined. In specific implementations, this can be a pair (key, value) - (key and value), or a link to such a pair, or a simple definition of a comparison operation on a required data structure or a link to it.
• For any X node, the properties of the search tree are executed: key [left [X]]

A binary search tree should not be confused with a binary heap built by different rules.

The main advantage of a binary search tree over other data structures is the possible high efficiency of the implementation of search and sort algorithms based on it.

The binary search tree is used to build more abstract structures, such as sets, multisets, associative arrays.

Content

• 1 Basic operations in a binary search tree
  • 1.1 Item Search (FIND)
  • 1.2 Adding an Item (INSERT)
  • 1.3 Removing a node (REMOVE)
  • 1.4 Tree Traversal (TRAVERSE)
  • 1.5 Splitting a tree by key
  • 1.6 Combining two trees into one
• 2 tree balancing
• 3 See also
• 4 Notes
• 5 References

Basic operations in a binary search tree

The basic interface of the binary search tree consists of three operations:

• FIND (K) - search for the node where the pair is stored (key, value) with key = K.
• INSERT (K, V) - adding to the tree a pair (key, value) = (K, V).
• REMOVE (K) - delete the node where the pair is stored (key, value) with key = K.

This abstract interface is a common case, for example, of such interfaces taken from applied tasks:

• “Phonebook” is a repository of records (the name of a person, his phone) with operations of searching and deleting records by the name of a person, and the operation of adding a new record.
• Domain Name Server - a repository of pairs (domain name, IP address) with modification and search operations.
• Namespace is a repository of variable names with their values, appearing in programming language translators.

In essence, a binary search tree is a data structure capable of storing a table of pairs (key, value) and supporting three operations: FIND, INSERT, REMOVE.

In addition, the binary tree interface includes three additional operations to traverse the tree nodes: INFIX_TRAVERSE, PREFIX_TRAVERSE, and POSTFIX_TRAVERSE. The first of them allows you to bypass the nodes of the tree in the order of non-decreasing keys.

Item Search (FIND)

Given : tree T and key K.

Task : check whether there is a node with key K in the T tree, and if so, return a link to this node.

Algorithm :

• If the tree is empty, report that the node was not found, and stop.
• Otherwise, compare K with the key value of the root node X.
  • If K = X, give a link to this node and stop.
  • If K> X, recursively look for the key K in the right subtree of T.
  • If K

Add item (INSERT)

Given : tree T and a pair (K, V).

Task : insert a pair (K, V) into the tree T (if K coincides, replace V).

Algorithm :

• If the tree is empty, replace it with a tree with one root node ((K, V), null, null) and stop.
• Otherwise, compare K with the root node key X.
  • If K> X, cyclically add (K, V) to the right subtree of T.
  • If K
  • If K = X, replace V of the current node with the new value. (although it is possible to organize a list of V values, but this is another topic)

Removing a node (REMOVE)

Given : tree T with root n and key K.

Task : remove the node with the key K from the tree T (if there is one).

Algorithm :

• If tree T is empty, stop;
• Otherwise, compare K with key X of root node n .
  • If K> X, cyclically remove K from the right subtree of T;
  • If K
  • If K = X, then it is necessary to consider three cases.
    • If there are no children, then delete the current node and reset the link to it from the parent node;
    • If one of the children is not present, then we put the values ​​of the child's fields m instead of the corresponding values ​​of the root node, overwriting its old values, and free the memory occupied by the node m ;
    • If both children are present, then
      • If the left node m of the right subtree is absent (n-> right-> left)
        • We copy from (8) to (4) the fields K, V and a link to the right node.
      • Otherwise
        • take the leftmost node m , the right subtree n-> right;
        • copy the data (except for links to child elements) from m to n ;
        • recursively remove the node m .

Tree Traversal (TRAVERSE)

There are three tree traversal operations that differ in the traversal order of the nodes.

The first operation, INFIX_TRAVERSE, allows you to bypass all the nodes of the tree in ascending order of keys and apply a user-defined callback function f, the operand of which is the node address, to each node. This function usually works only with a pair (K, V) stored in a node. The INFIX_TRAVERSE operation can be implemented in a recursive manner: first, it starts itself for the left subtree, then it starts this function for the root, then it starts it for the right subtree.

• INFIX_TRAVERSE (tr) - bypass the entire tree, following the order (left subtree, vertex , right subtree). Items ascending
• PREFIX_TRAVERSE (tr) - bypass the entire tree, following the order ( vertex , left subtree, right subtree). Items as in the tree
• POSTFIX_TRAVERSE (tr) - bypass the entire tree, following the order (left subtree, right subtree ', vertex ). Items in reverse order as in the tree

In other sources, these functions are named inorder, preorder, postorder, respectively [1]

INFIX_TRAVERSE

Given : tree T and function f

Task : apply f to all nodes of tree T in ascending order of keys

Algorithm :

• If the tree is empty, stop.
• Otherwise
  • Recursively bypass the left subtree T.
  • Apply f to the root node.
  • Recursively bypass the right subtree of T.

In the simplest case, the function f can output the value of a pair (K, V). When using the INFIX_TRAVERSE operation, all pairs will be displayed in ascending order of keys. If you use PREFIX_TRAVERSE, the pairs will be displayed in the order corresponding to the description of the tree given at the beginning of the article.

Splitting a tree by key

The “split tree by key” operation allows splitting one search tree into two: with keys < K 0 and ≥ K 0 .

Combining two trees into one

Reverse operation: there are two search trees, one has < K 0 keys, the other has ≥ K 0 . Combine them into one tree.

We have two trees: T 1 (smaller) and T 2 (larger). First you need to decide where to get the root: from T 1 or T 2 . There is no standard method, possible options:

• Take at random (see Cartesian wood).
• If the size of the entire branch is maintained at each node of the tree (see the tree with an implicit key), it is easy to estimate the imbalance for both options.

  alg Merging Trees (T1, T2)
 if T1 is empty, return T2
 if T2 is empty, return T1
 if you decide to make a T1 root, then
   T = Merging Trees (T1.right, T2)
   T1. right = T
   return t1
 otherwise
   T = Merging Trees (T1, T2.left)
   T2.left = T
   return t2

Tree balancing

It is always desirable that all paths in the tree from root to leaf be approximately the same length, that is, the depth of both the left and right subtrees is approximately the same in any node. Otherwise, performance is lost.

In a degenerate case, it may turn out that the entire left tree is empty at each level, there are only right trees, and in this case the tree degenerates into a list (going to the right). Search (and, therefore, deletion and addition) in such a tree is equal in speed to a search in the list and much slower than a search in a balanced tree.

For tree balancing, the operation “tree rotation” is used. Turning to the left looks like this:

• was Left (A) = L, Right (A) = B, Left (B) = C, Right (B) = R
• rotation swaps A and B, getting Left (A) = L, Right (A) = C, Left (B) = A, Right (B) = R
• the link that previously pointed to A also changes in the Parent (A) node, it points to B after the rotation.

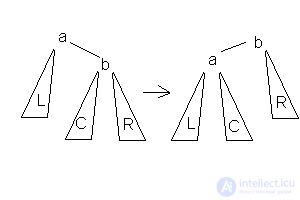
Turning to the right looks the same; it is enough to replace everything in the above example with Left to Right and back.

It is quite obvious that the rotation does not violate the orderliness of the tree, and has a predictable (+1 or −1) effect on the depths of all affected subtrees.

For deciding what kind of turns you need to make after adding or removing, use algorithms such as "red-ebony" and AVL.

Both of them require additional information in the nodes - 1 bit in red-black or a significant number in AVL.

A red-ebony tree requires <= 2 turns after adding and <= 3 after deletion, but the worst imbalance can be up to 2 times (the longest way is 2 times longer than the shortest one).

AVL-tree requires <= 2 turns after adding and to the depth of the tree after removal, but it is perfectly balanced (imbalance is not more than 1).

see also

• Associative array
• Cartesian tree
• Sort using a binary tree

Balanced trees:

• B-tree
• AVL-tree
• Red and black tree