Lecture
Semi-static data structures are characterized by the following features:
If we consider the semi-static structure at the logical level, then we can say about it that it is a sequence of data connected by linear list relations. Access to an element can be carried out by its serial number.
The physical representation of semi-static data structures in memory is usually a sequence of memory slots, where each next element is located in memory in the next slot (that is, a vector). The physical representation can also have the form of a unidirectional linked list (chain), where each next element is addressed by a pointer located in the current element. In the latter case, the restrictions on the length of the structure are much less stringent.
A stack is such a sequential list with variable length, the inclusion and exclusion of elements from which are performed only on one side of the list, called the top of the stack. Other stack names are also used - store and queue, which operates on the principle of LIFO (Last - In - First- Out - "last arrived - first excluded"). Examples of the stack: rifle cartridge shop, dead-end railway junction for sorting cars.
The main operations on the stack are the inclusion of a new element (the English name is push - push) and the elimination of the element from the stack (eng. Pop - pop up).
Ancillary operations may also be useful:
x: = pop (stack); push (stack, x).
Some authors also consider the inclusion / exclusion of elements for the middle of the stack, but the structure for which such operations are possible does not match the stack by definition.
For clarity, consider a small example that demonstrates the principle of the inclusion of elements in the stack and the exclusion of elements from the stack. In fig. Figure 4.1 (a, b, c) shows the states of the stack:
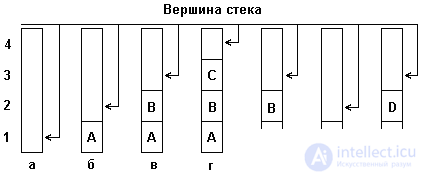
Figure 4.1. Inclusion and removal of items from the stack.
As can be seen from fig. 4.1, the stack can be represented, for example, in the form of a stack of books (elements) lying on a table. Give each book its own name, for example, A, B, C, D ... Then, at the time when there are no books on the table, the stack can be similarly said that it is empty. contains no items. If we start sequentially putting books one on top of another, then we get a stack of books (say, from n books), or we get a stack that contains n elements, and the top element is n + 1. Deletion of elements from the stack is carried out in a similar way, i.e., one element is deleted sequentially, starting from the top, or one book from the stack.
When a stack is represented in static memory, the memory is allocated for the stack as for a vector. In the descriptor of this vector, in addition to the usual parameters for the vector, there must also be a stack pointer — the address of the top of the stack. The stack pointer can point either to the first free stack element, or to the last item on the stack. (It doesn’t matter which of these two options to choose, it’s important later to strictly adhere to it when processing the stack.) In the future we will always assume that the stack pointer addresses the first free element and the stack grows towards increasing addresses.
When an element is pushed onto the stack, the element is written to the location indicated by the stack pointer, then the pointer is modified so that it points to the next free element (if the pointer points to the last written element, then the pointer is modified first and then the element is written). Modification of the pointer consists in adding a unit to it or in subtracting one from it (remember that our stack grows in the direction of increasing addresses.
The operation of eliminating an element consists in modifying the stack pointer (in the opposite direction to the modification when it is turned on) and fetching the value pointed to by the stack pointer. After sampling, the slot in which the selected item was placed is considered free.
The operation of clearing the stack is reduced to the entry in the stack pointer of the initial value — the address of the beginning of the allocated memory region.
Determining the size of the stack is reduced to calculating the difference between the pointers: the stack pointer and the address of the beginning of the area.
The software module presented in Example 4.1 illustrates stack operations that expand towards decreasing addresses. The stack pointer always points to the first free element.
In examples 4.1 and 4.3, it is assumed that the module will clarify the definitions of the structure size limit and data type for the structure element:
const SIZE = ...;
type data = ...;
{==== Software Example 4.1 ====}
{Stack}
unit stack;
Interface
const SIZE = ...; {stack size limit}
type data = ...; {emails can be of any type}
Procedure StackInit;
Procedure StackClr;
Function StackPush (a: data): boolean;
Function StackPop (Var a: data): boolean;
Function StackSize: integer;
Implementation
Var StA: array [1..SIZE] of data; {Stack - data}
{Pointer to the top of the stack, working on prefix subtraction}
top: integer;
Procedure StackInit; {** initialization - at the beginning}
begin top: = SIZE; end; {** clean = initialization}
Procedure StackClr;
begin top: = SIZE; end;
{** push item to stack}
Function StackPush (a: data): boolean;
begin
if top = 0 then StackPush: = false
else begin {enrollment, then increase pointer}
StA [top]: = a; top: = top-1; StackPush: = true;
end; end; {StackPush}
{** fetch item from stack}
Function StackPop (var a: data): boolean;
begin
if top = SIZE then StackPop: = false
else begin {pointer is incremented, then - selection}
top: = top + 1; a: = StA [top]; StackPop: = true;
end; end; {StackPop}
Function StackSize: integer; {** sizing}
begin StackSize: = SIZE-top; end;
End.
The stack is an extremely convenient data structure for many computing tasks. The most typical of these tasks is to provide nested procedure calls.
Suppose there is procedure A, which calls procedure B, and that in turn is procedure C. When procedure A reaches call B, procedure A pauses and control is transferred to the input point of procedure B. When B reaches call C, B is suspended and control is transferred to procedure C. When procedure C ends, control must be returned to B, and to the point following call C. At the end of B, control must return to A, to the point next to call B. Correct sequence nce Refunds easy to achieve if write the return address on the stack each time the procedure. So, when procedure A calls procedure B, the return address is placed on the stack at A; when B calls C, the return address of B is put on the stack. When C ends, the return address is selected from the top of the stack - and this is the return address of B. When B ends, the return address of A is at the top of the stack, and B returns from B A.
In the microprocessors of the Intel family, as in most modern processor architectures, a hardware stack is supported. The hardware stack is located in RAM, the stack pointer is contained in a pair of special registers - SS: SP, available to the programmer. The hardware stack expands in the direction of decreasing addresses; its pointer addresses the first free element. Executing the CALL and INT commands, as well as hardware interrupts, includes writing to the hardware return address stack. Executing the RET and IRET commands involves retrieving a return address from the hardware stack and transferring control to that address. A pair of commands - PUSH and POP - provides the use of the hardware stack for software solutions to other tasks.
Programming systems for block-oriented languages (PASCAL, C, etc.) use a stack to contain local variable procedures and other program blocks. With each activation of the procedure, memory for its local variables is allocated in the stack; at the end of the procedure, this memory is released. Since nesting is always strictly followed when calling procedures, there is always a memory at the top of the stack that contains local variables of the currently active procedure.
This technique makes it easy to implement recursive procedures. When a procedure calls itself, a new memory is allocated in the stack for all its local variables, and the nested call works with its own representation of local variables. When a nested call is completed, the memory space occupied by its variables in the stack is released and the presentation of the local variables of the previous level becomes relevant. Due to this, in the PASCAL and C languages any procedures / functions can call themselves. In the PL / 1 language, where other ways of locating local variables are assumed by default, the recursive procedure must be defined with the RECURSIVE handle — only then will its local variables be placed on the stack.
Recursion uses the stack in a hidden form from the programmer, but all recursive procedures can be implemented without recursion, but with an explicit use of the stack. In software example 3.17, the implementation of Hoar’s quick sort is shown in a recursive procedure. Software example 4.2 shows how another implementation of the same algorithm will look.
{==== Software Example 4.2 ====}
{Quick sort Hoare (stack)}
Procedure Sort (a: Seq); {see section 3.8}
type board = record {boundaries of the area being processed}
i0, j0: integer; end;
Var i0, j0, i, j, x: integer;
flag_j: boolean;
stack: array [1..N] of board; {stack}
stp: integer; {stack pointer works on zoom}
begin {common borders are put on the stack}
stp: = 1; stack [i] .i0: = 1; stack [i] .j0: = N;
while stp> 0 do {select borders from stack}
begin i0: = stack [stp] .i0; j0: = stack [stp] .j0; stp: = stp-1;
i: = i0; j: = j0; flag_j: = false; {pass permutations from i0 to j0}
while ia [j] then {permutation}
begin x: = a [i]; a [i]: = a [j]; a [j]: = x; flag_j: = not flag_j;
end;
if flag_j then Dec (j) else Inc (i);
end; if i-1> i0 then {insertion of the left boundary into the stack}
begin stp: = stp + 1; stack [stp] .i0: = i0; stack [stp] .j0: = i-1;
end; if j0> i + 1 then {inserting into the stack the boundaries of the right portion}
begin stp: = stp + 1; stack [stp] .i0: = i + 1; stack [stp] .j0: = j0;
end; end;
One pass sorting Hoare splits the original set into two sets. The boundaries of the resulting sets are stored in the stack. Then, from the stack, the boundaries located at the vertex are selected, and the set determined by these boundaries is processed. During its processing, a new pair of borders can be written onto the stack, etc. At the initial settings, the boundaries of the initial set are added to the stack. Sorting ends with the stack emptying.
The FIFO queue (First - In - First-Out - "first in, first out"). called such a sequential list with variable length, in which the inclusion of elements is performed only on one side of the list (this side is often called the end or tail of the queue), and the exception on the other side (called the beginning or head of the queue). Those queues to the counters and to the cash registers, which we do not like so much, are a typical everyday example of the FIFO queue.
The basic operations on the queue are the same as those on the stack — inclusion, exclusion, sizing, cleaning, non-destructive reading.
When representing a queue as a vector in static memory, in addition to the usual parameters for a vector descriptor, it must contain two pointers: to the beginning of the queue (to the first element in the queue) and to its end (the first free element in the queue). When an item is included in the queue, the item is written to the address specified by the end pointer, after which the pointer is incremented by one. When an item is excluded from the queue, an item is selected that is addressed by a pointer to the beginning, after which this pointer is decremented by one.
Obviously, over time, the pointer to the end when the element is next turned on will reach the upper boundary of the memory area allocated for the queue. However, if the turn on operations alternated with the operations of excluding elements, then in the initial part of the memory allocated for the queue there is free space. In order for the places occupied by the excluded elements to be reused, the queue is closed in a ring: the pointers (at the beginning and at the end), having reached the end of the allocated memory area, are switched to its beginning. This queuing in memory is called a ring queue. Of course, other organization options are possible: for example, whenever the end pointer reaches the upper memory limit, move all non-empty elements of the queue to the beginning of the memory area, but both this and other options require moving the elements of the queue in memory and are less effective. than ring line.
In the initial state, the start and end pointers indicate the beginning of the memory area. The equality of these two pointers (for any value) is a sign of an empty queue. If in the process of working with a ring queue the number of enable operations exceeds the number of exclusion operations, then a situation may arise in which the end pointer will "catch up" with the start pointer. This is a full queue situation, but if the pointers are equal in this situation, this situation will be indistinguishable from the empty queue situation. To distinguish these two situations, the ring queue is required to have a “gap” of free elements between the end pointer and the start pointer. When this “gap” is reduced to one item, the queue is considered full and further attempts to write to it are blocked. Clearing a queue reduces to writing the same (not necessarily initial) value to both pointers. Sizing consists in calculating the difference of pointers taking into account the ring nature of the queue.
Program example 4.3 illustrates queuing and operations on it.
{==== Program Example 4.3 ====}
unit queue; {FIFO queue - ring}
Interface
const SIZE = ...; {queue size limit}
type data = ...; {emails can be of any type}
Procesure QInit;
Procedure Qclr;
Function QWrite (a: data): boolean;
Function QRead (var a: data): boolean;
Function Qsize: integer;
Implementation {Queue on the ring}
var QueueA: array [1..SIZE] of data; {queue data}
top, bottom: integer; { beginning and the end }
Procedure QInit; {** initialization - start = end = 1}
begin top: = 1; bottom: = 1; end;
Procedure Qclr; {** clean - start = end}
begin top: = bottom; end;
Function QWrite (a: data): boolean; {** write to end}
begin
if bottom mod SIZE + 1 = top then {the queue is full} QWrite: = false
else begin
{record, modification of pointers.end with the transition to the ring}
Queue [bottom]: = a; bottom: = bottom mod SIZE + 1; QWrite: = true;
end; end; {QWrite}
Function QRead (var a: data): boolean; {** fetch from start}
begin
if top = bottom then QRead: = false else
{record, modification, decree. start with moving around the ring}
begin a: = Queue [top]; top: = top mod SIZE + 1; QRead: = true;
end; end; {QRead}
Function QSize: integer; {** sizing}
begin
if top <= bottom then QSize: = bottom-top
else QSize: = bottom + SIZE-top;
end; {QSize}
End.
In real-world tasks, it sometimes becomes necessary to form queues other than FIFO or LIFO. The order of selection of elements from such queues is determined by the priorities of the elements. The priority in the general case can be represented by a numerical value, which is calculated either on the basis of the values of any element fields, or on the basis of external factors. So, both the FIFO and LIFO queues can be interpreted as priority queues, in which the priority of an element depends on the time it is included in the queue. When an item is selected, the item with the highest priority is selected each time.
Priority queues can be implemented on linear list structures - in an adjacent or connected view. Queues with priority inclusion are possible - in which the sequence of elements of the queue is kept ordered all the time; each new element is included in the place in the sequence, which is determined by its priority, and with the exception, the element is always selected from the beginning. Queues with a priority exception are also possible - a new element is always included at the end of the queue, and if an exception is in the queue, the element with the highest priority is searched for (this search can only be linear) and after sampling is removed from the sequence. And in fact, and in another embodiment, a search is required, and if the queue is placed in static memory - also the movement of elements.
The most convenient form for organizing large queues with priorities is the sorting of elements by decreasing priorities by a partially ordered tree, which we considered in section 3.9.2.
An ideal example of a ring queue in a computing system is the keyboard buffer in the Basic PC I / O System of an IBM PC. The keyboard buffer occupies a sequence of bytes of memory at addresses from 40: 1E to 40: 2D, inclusive. At addresses 40: 1A and 40: 1C are located pointers to the beginning and end of the queue, respectively. When you press any key, an interrupt 9 is generated. The interrupt handler reads the code of the pressed key and places it in the keyboard buffer - at the end of the queue. Keycodes can accumulate in the keyboard buffer before they are read by the program. The program when entering data from the keyboard refers to the interrupt 16H.The handler for this interrupt selects the key code from the buffer — from the beginning of the queue — and sends it to the program.
The queue is one of the key concepts in multi-tasking operating systems (Windows NT, Unix, OS / 2, EU, etc.). The resources of the computing system (processor, RAM, external devices, etc.) are used by all tasks simultaneously performed in the environment of such an operating system. Since many types of resources do not allow real simultaneous use by different tasks, such resources are provided to tasks alternately. tasks claiming to use one resource or another are lined up for this resource.These queues are usually priority ones, however, FIFO queues are often used as well, since this the only logical organization of the queue, which is guaranteed not to allow the constant displacement of the task of higher priority.LIFO queues are typically used by operating systems to account for free resources.
Also in modern operating systems, one of the means of interaction between parallel tasks performed is message queues, also called mailboxes. Each task has its turn - a mailbox, and all messages sent to it from other tasks fall into this queue. The task owner of the queue selects messages from it, and can control the order of the selection — FIFO, LIFO, or by priority.
Dec is a special kind of queue. Dec (from the English. Deq - double ended queue, ie, the queue with two ends) - this is a sequential list in which both the inclusion and exclusion of elements can be carried out from either of the two ends of the list. A special case of deck - decks with limited input and decks with limited output. The logical and physical structures of the deck are similar to the logical and physical structure of the ring FIFO queue. However, with respect to the deck, it is advisable to speak not of the beginning and the end, but of the left and right end.
Deck operations:
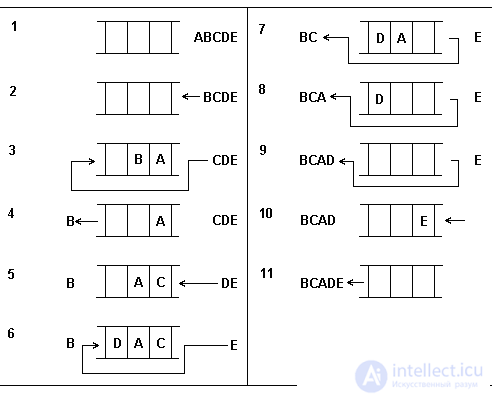
Fig. 4.2. The states of the deck are in the process of changing.
In fig.4.2. As an example, the sequence of decks states is shown when five elements are turned on and removed. At each stage, the arrow indicates from which end of the deck (left or right) the element is included or excluded. The elements are respectively labeled A, B, C, D, E.
The physical structure of the deck in static memory is identical to the structure of the ring queue. It is not difficult to develop a software example illustrating the organization of the deck and operations on it, following the examples of examples 4.1, 4.3. Procedures and functions must be implemented in this module:
Function DeqWrRight (a: data): boolean; - the inclusion of the element to the right;
Function DeqWrLeft (a: data): boolean; - the inclusion of the element on the left;
Function DeqRdRight (var a: data): boolean; - exclusion of the element to the right;
Function DeqRdLeft (var a: data): boolean; - exclusion of the element to the left; Procedure DeqClr; - cleaning;
Function DeqSize: integer; - determination of size.
Tasks requiring a deck structure are found in computing and programming much less frequently than tasks implemented on a stack or queue structure. As a rule, the entire organization of a deque is performed by a programmer without any special means of system support.
However, as an example of such system support, consider the organization of the input buffer in the REXX language. In normal mode, the input buffer is connected to the keyboard and works as a FIFO queue. However, in REXX, it is possible to assign a software buffer as an input buffer and send the output of programs and system utilities to it. The programmer has the following operations: QUEUE - writing a string to the end of the buffer and PULL - fetching a string from the beginning of the buffer. An additional PUSH operation — writing a string to the beginning of the buffer — turns the buffer into decks with limited output. This input buffer structure allows programming a very flexible pipelining on the REXX with the direction of output of one program to the input of another and modification of the redirected flow.
A string is a linearly ordered sequence of characters belonging to a finite set of characters, called the alphabet.
Strings have the following important properties:
Speaking of strings, they usually mean text strings — strings consisting of characters in the alphabet of a selected language, numbers, punctuation marks, and other official characters. Indeed, the text line is the most universal form of presenting any information: today the entire amount of information accumulated by mankind - from the Old Testament to our textbook - is presented in the form of text lines. In our further examples in this section, we will work with text strings. However, it should be borne in mind that the characters included in the string may belong to any alphabet. Thus, in the PL / 1 language, along with the data type "character string" - CHAR (n) - there is a data type "bit string" - BIT (n). Bit strings are composed of 1-bit characters belonging to the alphabet:{0, 1}. All string operations apply equally well to both character and bit strings.
Encoding of symbols was considered in Chapter 2. Note that, depending on the specifics of the task, the properties of the used alphabet and the language it represents, and the properties of storage media, other ways of encoding characters can be used. In modern computing systems, however, the coding of the entire set of characters on a fixed-size discharge grid (1 byte) is universally accepted.
Although the lines are discussed in the chapter devoted to semi-static data structures, in some specific tasks, the variability of the lines can vary from completely unavailable to practically unlimited possibilities for change. The orientation on one or another degree of variability of strings determines both their physical representation in memory and the peculiarities of performing operations on them. In most programming languages (C, PASCASL, PL / 1, etc.), strings are represented as semi-static structures.
Depending on the orientation of the programming language, string tools occupy a more or less significant place in the language. Consider three examples of string handling.
The C language is a system programming language, the data types with which the C language works are as close as possible to the types with which the machine commands work. Since machine instructions do not work with strings, there is no such type of data in the C language. Strings in C are represented as arrays of characters. Operations on strings can be performed as array processing operations or with the help of library (but not built-in!) String processing functions.
In universal languages, usually the string type is basic in the language: STRING in PASCAL, CHAR (n) in PL / 1. (In PASCAL, the length of a string declared in this way can vary from 0 to n, in PL / 1, so that the length of a string can change, it must be declared with a VARING handle.) Basic operations on strings are implemented as simple operations or built-in functions. Libraries that provide an extended set of string operations are also possible.
REXX language is focused primarily on the processing of textual information. Therefore, in REXX, there is no means for describing data types: all data is represented as character strings. Operations on data that are not inherent in character strings are either performed by special functions or result in a type conversion that is transparent to the programmer. So, for example, the REXX interpreter, having encountered an operator containing an arithmetic expression, itself translates its operands into a numeric type, evaluates the expression and converts the result into a character string. A number of string operations are simple language operations, and there are several dozen built-in string processing functions in REXX.
The basic operations on strings are:
The operation of determining the length of a string has the form of a function whose return value is an integer number - the current number of characters in the string. The assignment operation has the same meaning as for other data types.
The string comparison operation has the same meaning as for other data types. String comparison is performed according to the following rules. The first characters of the two lines are compared. If the characters are not equal, then the string containing the character, whose place in the alphabet closer to the beginning, is considered smaller. If the characters are equal, the second, third, etc. are compared. characters. When one end of one of the lines is reached, a line shorter than that is considered smaller. In case of equal lengths of lines and pairwise equality of all characters in them, the lines are considered equal.
The result of concatenating two strings is a string whose length is equal to the total length of the operand strings, and the value corresponds to the value of the first operand, immediately followed by the value of the second operand. The clutch operation gives the result, the length of which is generally greater than the lengths of the operands. As with all operations on strings, which can increase the length of a string (assignment, chaining, complex operations), it is possible that the result will be longer than the memory allocated for it. Naturally, this problem occurs only in those languages where the string length is limited. There are three possible solutions to this problem, determined by the rules of the language or compilation modes:
The operation of extracting a substring selects a sequence of characters from the source line, starting at a given position n, with a given length l. In PASCAL, the corresponding function is called COPY. In PL / 1, REXX, the corresponding function, SUBSTR, has an interesting feature that is missing from PASCAL. The SUBSTR function can be used *** in the left part of an assignment operator. For example, if the initial value of some string S is 'ABCDEFG', then the execution of the statement: SUBSTR (S, 3,3) = '012'; change the value of string S to - 'AB012FG'.
When implementing the operation of allocating a substring in the programming language and in the user procedure, the rule of obtaining the result must be defined for the case when the initial position n is set such that the part of the original string remaining behind it has a length less than the specified length l, or even n exceeds the length of the original lines. Possible options for this rule:
The operation of finding the entry finds the place of the first occurrence of the reference substring in the source string. The result of the operation can be a position number in the source line from which the reference entry begins or a pointer to the beginning of the entry. If there is no occurrence, the result of the operation must be some special value, for example, a zero position number or a null pointer.
Based on the basic operations, any other, even complex string operations can be implemented. For example, the operation of deleting characters from the string n1 inclusively n2 can be implemented as a sequence of the following steps:
However, in order to increase efficiency, some secondary operations can also be implemented as basic ones - using our own algorithms, with direct access to the physical structure of the string.
The representation of lines in memory depends on how volatile the lines are in each specific task, and the means of such a representation vary from absolutely static to dynamic. Universal programming languages generally provide work with variable-length strings, but the maximum string length must be specified when creating it. If the programmer is not satisfied with the capabilities or effectiveness of those tools for working with strings that the programming language provides him, then he can either define his data type "string" and use the dynamic memory management tools to represent it, or change the programming language to a specially oriented processing. text (CNOBOL, REXX), in which the string representation is based on dynamic memory management.
VECTOR PRESENTATION OF LINES.
The representation of lines in the form of vectors, adopted in most universal programming languages, allows you to work with strings located in static memory. In addition, the vector representation makes it easy to refer to individual characters of a string as elements of a vector — by index.
The simplest way is to represent a string as a vector of constant length. In this case, a fixed number of bytes in which the characters of the string are written are allocated in the memory. If the line is less than the vector allocated for it, then the extra space is filled with spaces, and if the line is outside the vector, then the extra characters (usually to the right of the lines) should be discarded.
Fig. 4.3 shows a diagram showing the representation of two lines: 'ABCD' and 'PQRSTUVW' as a vector of constant length by six characters.

Fig. 4.3. String representation by constant length vectors
PRESENTATION OF THE LINES BY THE VECTOR OF A VARIABLE LENGTH WITH A SIGN OF END.
This and all subsequent methods take into account the variable length of the lines. The end sign is a special character belonging to the alphabet (thus, the useful alphabet is less than one character), and occupies the same number of digits as all other characters. The memory cost of this method is 1 character per line. Such a string representation is shown in Fig.4.4. The special character-marker of the end of the line is designated here as 'eos'. In C, for example, a character with a code of 0 is used as a line end marker.

Fig. 4.4. Variable-length string representation with an end sign.
PRESENTING THE LINES BY THE VECTOR OF A VARIABLE LENGTH WITH A COUNTER.
The character counter is an integer, and enough bits are allocated for it to be enough to represent the length of the longest string that can be represented in this machine. Usually, the counter is allocated from 8 to 16 bits. Then, with this view, the memory cost per line is 1-2 characters. When using the character counter, random access to the characters within the string is possible, as you can easily check that the reference does not go beyond the string. The counter is located in a place where it can be easily accessed - at the beginning of a line or in a line descriptor. The maximum possible string length is thus limited by the counter width. In PASCAL, for example, a string is represented as an array of characters, the index in which starts from 0; The one-byte counter for the number of characters in a string is the zero element of this array. Such a string representation is shown in Fig.4.5. Both the symbol counter and the terminator in the previous case can be accessed by the programmer as elements of a vector.

Fig.4.5. Representation of variable length strings with a counter
In the two previous versions, the most efficient use of memory was ensured (1-2 “extra” characters per line), but the variability of the line was provided extremely inefficiently. Since a vector is a static structure, each change in the length of a line requires the creation of a new vector, sending the unchanged part of the line to it and destroying the old vector. This negates all the benefits of working with static memory. Therefore, the most popular way to represent lines in memory are vectors with controlled length.
VECTOR WITH MANAGED LENGTH.
Memory for a vector with a controlled length is allocated when creating a string and its size and location remain unchanged throughout the life of the string. In the descriptor of such a row vector, there may be no initial index, since it can be fixed once for all established agreements, but the field of the current length of the string appears. The row size can thus vary from 0 to the value of the maximum vector index. The "extra" part of the memory can be filled with any codes - it is not taken into account when operating with a string. The final index field can be used to control whether the line has exceeded the amount of allocated memory. The representation of lines as a vector with controlled length (with a maximum length of 10) is shown in Fig.4.6.
Although such a string representation does not save memory, programmers of programming systems, as can be seen, consider this an acceptable price to be able to work with changeable strings in static memory.
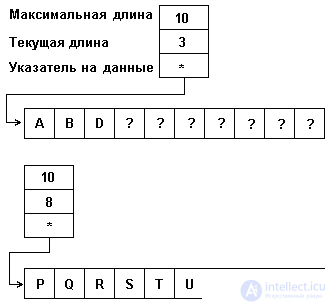
Fig.4.6. Representation of lines by a vector with controlled length
In program example 4.4, a module is introduced that implements the representation of lines by a vector with a controlled length and some operations on such lines. To reduce the volume in the example, not all procedures / functions are defined in the Implementation section. We provide the reader to independently develop other subprograms announced in the Interface section. The string descriptor is described by the _strdescr type, which exactly repeats the structure shown in Fig.4.6. The NewStr function allocates two memory areas: for the row descriptor and for the row data area. The address of the string descriptor returned by the NewStr function — the varstr type — is the variable whose value is specified by the module user to identify a specific string during all subsequent operations with it. The data area, the pointer to which is entered in the string descriptor - type _dat_area - is described as an array of characters of the maximum possible size - 64 KB. However, the amount of memory allocated for the data area by the NewStr function is usually smaller - it is specified by the function parameter. Although the indexes in the array of characters of a string can theoretically vary from 1 to 65535, the value of the index in each specific string during its processing is limited to the maxlen field of the handle of this string. All procedures / functions of processing strings work with string characters as with vector elements, referring to them by index. The address of the procedure vector is obtained from the string handle. Note that in the CopyStr procedure, the length of the result is limited to the maximum length of the target string.
{==== Software Example 4.4 ====}
{Representation of lines by a vector with a controlled length}
Unit Vstr;
Interface
type _dat_area = array [1..65535] of char;
type _strdescr = record {string handle}
maxlen, curlen: word; {maximum and current length}
strdata: ^ _dat_area; {pointer to the given strings}
end;
type varstr = ^ _strdescr; {type - LINE VARIABLE LINE}
Function NewStr (len: word): varstr;
Procedure DispStr (s: varstr);
Function LenStr (s: varstr): word;
Procedure CopyStr (s1, s2: varstr);
Function CompStr (s1, s2: varstr): integer;
Function PosStr (s1, s2: varstr): word;
Procedure ConcatStr (var s1: varstr; s2: varstr);
Procedure SubStr (var s1: varstr; n, l: word);
Implementation
{** string creation; len is the maximum length of a string;
f-tion returns a pointer to a string handle}
Function NewStr (len: word): varstr;
var addr: varstr;
daddr: pointer;
begin
New (addr); {allocate memory for descriptor}
Getmem (daddr, len); {allocating memory for data}
{entry in the descriptor of the initial values}
addr ^ .strdata: = daddr; addr ^ .maxlen: = len; addr ^ .curlen: = 0;
Newstr: = addr;
end; {Function NewStr}
Procedure DispStr (s: varstr); {** Destroy a string}
begin
FreeMem (s ^ .strdata, s ^. Maxlen); {data destruction}
Dispose (s); {kill the handle}
end; {Procedure DispStr}
{** Determine the length of the string, the length is selected from the descriptor}
Function LenStr (s: varstr): word;
begin
LenStr: = s ^ .curlen;
end; {Function LenStr}
Procedure CopyStr (s1, s2: varstr); {Assignment of strings s1: = s2}
var i, len: word;
begin
{length of result string, m. limited to its max. long}
if s1 ^ .maxlen s2; -1 if s1 <s2} function="" compstr="" (s1,="" s2:="" varstr):="" integer;="" var="" i:="" begin="" {current="" character="" index}="" {cycle="" until="" the="" end="" of="" one="" lines="" is="" reached}="" while="" (i="" <="s1" ^="" .curlen)="" and="" do="" {if="" i'th="" characters="" are="" not="" equal,="" ends}="" if="" s1="" .strdata="" [i]=""> s2 ^ .strdata ^ [i] then
begin CompStr: = 1; Exit; end;
if s1 ^ .strdata ^ [i]
{if the execution reached this point, then the end of one of the lines was found, and all the characters so far compared were equal; a shorter string is considered shorter}
if s1 ^ .curlen s2 ^ .curlen then CompStr: = 1
else CompStr: = 0;
end; {Function CompStr}
.
.
End.
SYMBOL - CONNECTED REPRESENTATION OF LINES.
The list representation of strings in memory provides flexibility in performing various operations on strings (in particular, operations of including and excluding individual characters and entire chains) and the use of system memory management tools in allocating the necessary memory for the string. However, this incurs additional memory costs. Another disadvantage of the list view of a string is that the logically adjacent elements of the string are not physically adjacent in memory. This complicates access to groups of line elements compared to access in the vector representation of a line.
SINGLE-DIRECTIONAL LINEAR LIST.
Each character of the string is represented as an element of a linked list; the element contains the character code and a pointer to the next element, as shown in Fig.4.7. One-way grip represents access in only one direction along the line. For each character of the string, one pointer is required, which usually takes 2-4 bytes.

Fig.4.7. Representation of a string by a unidirectional linked list
BILATERAL LINEAR LIST.
A pointer to the previous element is also added to each element of the list, as shown in Figure 4.8. Bilateral coupling allows two-way movement along the list, which can significantly improve the efficiency of performing some string operations. In this case, for each character of the string, two pointers are needed, i.e. 4-8 bytes.

Fig.4.8. String representation of a bidirectional linked list
BLOCK - CONNECTING THE LINE.
This representation allows in most operations to avoid the costs associated with managing dynamic memory, but at the same time provides a fairly efficient use of memory when working with strings of variable length.
MULTYMBROST LINKS OF FIXED LENGTH.
Multi-character groups (links) are organized into a list, so each list item, except the last one, contains a group of line items and a pointer to the next list item. The pointer field of the last element of the list stores the end character - a null pointer. In the course of processing, lines from any position can be eliminated or elements are inserted anywhere, as a result of which links can contain fewer elements than they were originally. For this reason, a special character is needed that would indicate the absence of an element at the corresponding line position. Denote such a symbol 'emp', it should not be included in the set of characters from which the string is organized. An example of multi-character links of fixed length of 4 characters per link is shown in Figure 4.9.
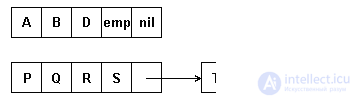
Fig. 4.9. String representation of multi-character links of constant length
Such a representation provides a more efficient use of memory than symbol-related. In some cases, insert / delete operations can be reduced to inserting / deleting whole blocks. However, if you delete single characters in blocks, empty emp characters can accumulate, which can even lead to worse memory usage than in a character-based representation.
MULTIBELAND LINKS OF A VARIABLE LENGTH.
The variable block length makes it possible to get rid of empty characters and thereby save memory for the string. However, there is a need for a special character - a sign of the pointer, in Figure 4.10 it is indicated by the symbol 'ptr'.
With the increase in the length of groups of characters stored in blocks, the efficiency of memory use increases. However, a negative characteristic of the method under consideration is the complication of operations for reserving memory for list items and returning vacated items to the general list of available memory.
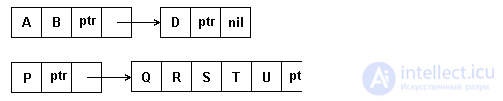
Fig.4.10. String representation of multi-character variable length links
This method of list representation of strings is especially useful in text editing tasks, when most of the operations involve changing, inserting and deleting whole words. Therefore, in these tasks it is advisable to organize the list so that each element contains one word of text. Space characters between words in memory may not be represented.
MULTYMBOLIC LINKS WITH CONTROLLABLE LENGTH.
Memory is allocated blocks of fixed length. In each block, in addition to the characters of the line and the pointer to the next block, the numbers of the first and last characters in the block are contained. When processing a line in each block, only characters located between these numbers are processed. The empty character is not used: when a character is removed from a string, the remaining characters in the block are compressed and the boundary numbers are adjusted. The symbol can be inserted due to the free space available in the block, and in the absence of one, by inserting a new block. Although insert / delete operations require the transfer of characters, the transfer range is limited to one block. At each change operation, the occupancy of neighboring blocks can be analyzed and two half-empty neighboring blocks can be re-formed into one block. To determine the end of the line can be used as a null pointer in the last block, and a pointer to the last block in the line descriptor. The latter can be very useful when performing certain operations, for example, coupling. The length of the string can also be stored in the descriptor: it is more convenient to read it from the descriptor than to count it by iterating over all blocks of the string.
An example of the representation of a string as links with a controllable length of 8 is shown in Figure 4.11.
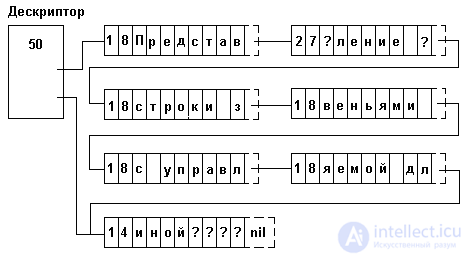
Fig.4.11. Representation of a string by links of controlled length
In program example 4.5, a module is introduced that implements the representation of strings by links with controlled length. Even at first glance it is clear that it is much more complicated than Example 4.4. This is explained by the fact that there are forced to process both connected (lists of blocks) and vector (array of characters in each block) structures. Therefore, when sequentially processing characters in a string, the procedure must store both the address of the current block and the number of the current character in the block. For these purposes, all the procedures / functions use the variables cp and bi, respectively. (Procedures and functions that process two strings — cp1, bi1, cp2, bi2.) The string descriptor — type _strdescr — and block — type _block — exactly repeat the structure shown in Figure 4.10. The NewStr function allocates memory only for the string descriptor and returns the address of the descriptor — the varstr type — it serves as the string identifier for subsequent operations with it. Memory for storing row data is allocated only as needed. All procedures / functions have the following rules for working with memory:
To release the blocks, a special internal FreeBlock function is defined, which frees the entire list of blocks, the head of which is given by its parameter.
Note that in no procedure the maximum volume of the result string is controlled - it can be arbitrarily large, and the length field in the string descriptor is of type longint.
{==== Software Example 4.5 ====}
{Representation of the string by links of controlled length}
Unit Vstr;
Interface
const BLKSIZE = 8; {number of characters in the block}
type _bptr = ^ _block; {pointer to block}
_block = record {block}
i1, i2: byte; {numbers of the 1st and last characters}
strdata: array [1..BLKSIZE] of char; {characters}
next: _bptr; {pointer to the next block}
end;
type _strdescr = record {string handle}
len: longint; {string length}
first, last: _bptr; {decree on the 1st and last blocks}
end;
type varstr = ^ _strdescr;
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.