Lecture
| Red and black tree | ||
|---|---|---|
| Type of | search tree | |
| Invented in | 1972 | |
| Invented | Rudolf Bayer | |
| Time complexity in O-symbolism |
||
| Average | At worst | |
| Memory consumption | O (n) | O (n) |
| Search | O (log n) | O (log n) |
| Insert | O (log n) | O (log n) |
| Deletion | O (log n) | O (log n) |
Binary search trees of height implement all basic operations on dynamic sets in time O (h). Thus, operations are performed the faster, the smaller the height of the tree. However, in the worst case, the performance of a binary search tree is no better than the performance of a linked list. Red-black trees are one of the many “balanced” schemes of search trees that guarantee the execution time of operations on the dynamic set O (lg n) even in the worst case.
Red-Black Tree (English Red-Black-Tree , RB-Tree ) is one of the self-balancing binary search trees that guarantee a logarithmic growth of the tree height from the number of nodes and quickly performs basic operations of the search tree: adding, deleting and searching for a node. The balance is achieved by introducing an additional attribute of the tree node - “colors”. This attribute can take one of two possible values - “black” or “red”.
The inventor of the red-ebony consider the German Rudolf Bayer. The name "red-ebony" data structure received in the article L. Gimpasa and R. Sedzhvika (1978). Two colors (red and black) [1] were available in the magazine, and the extra bit “attached” to each of the nodes was indicated by color.
A red and black tree is a special kind of binary tree used in computer science to organize comparable data, such as fragments of text or numbers. Leaf nodes of red-black trees do not contain data. Such leaves do not need explicit memory allocation — a null pointer to the child can actually mean that this child is a leaf node, but in some cases working with red-black trees, using explicit leaf nodes can serve as a simplification of the algorithm.
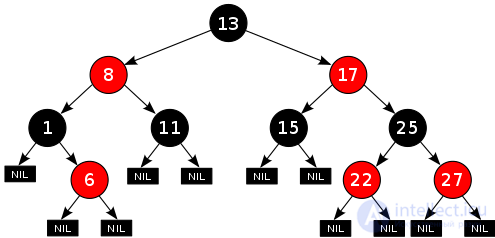
An example of red and black wood
A red-black tree is a binary search tree in which each node has a color attribute that takes on the values red or black . In addition to the usual requirements imposed on binary search trees, the following requirements apply to red-black trees:
These restrictions realize the critical property of red-black trees: the path from the root to the farthest leaf is no more than two times longer than the path from the root to the nearest leaf (if the farthest leaf is located at the 3rd level). The result is that the tree is roughly balanced. Since such operations as inserting, deleting, and searching for values require, at worst, time proportional to the length of the tree, this theoretical upper limit of height allows red-black trees to be more efficient at worst than regular binary search trees.
To understand why this is guaranteed, it suffices to consider the effect of properties 4 and 5 together. Suppose that for a red-black tree T the number of black nodes in property 5 is B. Then the shortest possible path from the root of the tree T to any leaf node contains B black nodes. A longer possible path can be constructed by including red nodes. However, property 4 does not allow inserting several red nodes in a row. Therefore, the longest possible path consists of 2B nodes, alternately red and black. Any maximum path has the same number of black nodes (by property 5), therefore, there is no path more than twice as long as any other path.
In many implementations of the tree structure, it is possible that a node has only one descendant and the leaf node contains data. Under these assumptions, it is possible to realize a red-ebony, but several properties will change and the algorithm will become more complicated. For this reason, this article uses “fake leaf nodes” that do not contain data and simply serve to indicate where the tree ends. These nodes are often omitted when the graphic image, as a result, the tree looks contradictory with the above principles, but in fact there is no contradiction. The consequence of this is that all internal (non-leaf) nodes have two descendants, although one of them may be a zero sheet. Property 5 ensures that a red node must have either two black zero sheets as descendants or two black internal nodes. For a black node with one descendant null leaf node and another non-descendant, properties 3, 4 and 5 ensure that the latter must be a red node with two black zero leaves as descendants.
Sometimes a red-black tree is interpreted as a binary search tree, which has edges instead of nodes in red and black colors, but this does not have any meaning. The color of the node in terms of this article corresponds to the color of the edge connecting the node with its ancestor, except that the root node is always black (property 2), while the corresponding edge does not exist.
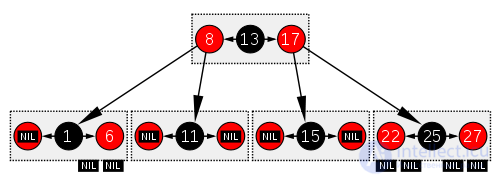
The same red-black tree as in the example above, represented as a B-tree.
The red-ebony tree is similar in structure to the B-tree with parameter 2, in which each node can contain from 1 to 3 values and, accordingly, from 2 to 4 pointers to descendants. In such a B-tree, each node will contain only one value corresponding to the value of the black node of the red-black tree with optional values before and / or after it in the same node, both of which correspond to the equivalent red nodes of the red-black tree.
One way to see this equivalence is to “raise” red nodes in a graphical representation of a red-black tree so that they are flush with their ancestors black nodes, forming a page. In the B-tree, or in a modified graphical representation of a red-black tree, all the leaf nodes have the same depth.
This type of B-tree is more common than a red-black tree, although, as can be seen, several red-black trees can be obtained from one such B-tree with parameter 2. If the B-tree page contains only one value, this node is black and has two children. If the page contains three values, the central node is black, and each of its neighbors is red. However, if the page contains two values, any node can become black in a red-black tree (and then the second will be red).
Red-black trees are among the most actively used in practice, self-balancing search trees. In particular, the set and map containers in most implementations of the STL library of the C ++ language [2] , the TreeMap class of the Java language [3] , as well as many other implementations of the associative array in various libraries, are based on red-black trees.
The popularity of red-black trees is due to the fact that they often achieve a suitable balance between the degree of balance and the difficulty of maintaining balance. In particular, when comparing with perfectly balanced trees, it is often found that the latter have too strict a condition of balance and when performing removal operations from a tree a lot of time is spent on maintaining the necessary balance.
Reading operations for a red-black tree are no different from others for a binary search tree, because any red-black tree is a special case of a regular binary search tree. However, the immediate result of insertion or deletion may lead to a violation of the properties of red-black trees. Restoration of properties requires a small (O (log n ) or O (1)) number of color change operations (which is very fast in practice) and no more than three tree turns (no more than two for insertion). Although insertion and deletion are complex, their complexity remains O (log n ).
Insertion starts with adding a node, just like in a regular binary search tree, and dyeing it in red. But if in the binary search tree we always add a leaf, in a red-black tree the leaves do not contain data, therefore we add a red internal node with two black descendants in place of the black leaf.
What happens next depends on the color of nearby sites. The term uncle will be used to refer to the brother of the parent node, as in the family tree. Notice, that:
Note : The letter N will denote the current node (colored red). At first this is a new node that is inserted, but this procedure can be recursively applied to other nodes (see case 3). P we denote the ancestor of N , G denotes the grandfather N , and U we denote uncle N. Note that in some cases, the roles of nodes may change, but, in any case, each designation will represent the same node as in the beginning. Any color depicted in the figure is either assumed in this case, or is obtained from other considerations.
Each case is considered with examples of C code. The uncle and grandfather of the current node can be found using functions:
struct node *
grandparent (struct node * n)
{
if ((n! = NULL) && (n-> parent! = NULL))
return n-> parent-> parent;
else
return NULL;
}
struct node *
uncle (struct node * n)
{
struct node * g = grandparent (n);
if (g == NULL)
return NULL; // No grandparent means no uncle
if (n-> parent == g-> left)
return g-> right;
else
return g-> left;
}
Case 1: The current node is N in the root of the tree. In this case, it is repainted to black to leave Property 2 (Root - black) true. Since this action adds one black node to each path, Property 5 (All paths from any given node to leaf nodes contain the same number of black nodes) is not violated.
void
insert_case1 (struct node * n)
{
if (n-> parent == NULL)
n-> color = BLACK;
else
insert_case2 (n);
}
Case 2: The ancestor P of the current node is black, that is, Property 4 (Both descendants of each red node are black) is not violated. In this case, the tree is valid. Property 5 (All paths from any given node to leaf nodes contain the same number of black nodes) is not violated, because the current node N has two black leaf descendants, but since N is red, the path to each of these descendants contains the same number of black nodes as the path to the black sheet, which was replaced by the current node, so the property remains true.
void
insert_case2 (struct node * n)
{
if (n-> parent-> color == BLACK)
return; / * Tree is still valid * /
else
insert_case3 (n);
}
Note: In the following cases, it is assumed that N has a grandfather G , since his parent P is red, and if he was a root, he would be painted black. Thus, N also has Uncle U , although he may be a leaf node in cases 4 and 5.
|
Case 3: If both parent P and uncle U are red, then both of them can be repainted black and grandfather G turns red (to save property 5 (All paths from any given node to leaf nodes contain the same number of black nodes)). Now the current red node N has a black parent. Since any path through a parent or uncle must pass through a grandfather, the number of black nodes in these paths will not change. However, grandfather G can now break properties 2 (Root - black) or 4 (Both descendants of each red node are black) (property 4 can be broken, since the parent G can be red). To fix this, the whole procedure is recursively executed on G from case 1. |
void
insert_case3 (struct node * n)
{
struct node * u = uncle (n), * g;
if ((u! = NULL) && (u-> color == RED) && (n-> parent-> color == RED)) {
n-> parent-> color = BLACK;
u-> color = BLACK;
g = grandparent (n);
g-> color = RED;
insert_case1 (g);
} else {
insert_case4 (n);
}
}
Note: In the remaining cases, it is assumed that the parent P is the left descendant of its ancestor. If this is not the case, you need to change left and right . Code samples will take care of this.
|
Case 4: P's parent is red, but Uncle U is black. Also, the current node N is the right descendant of P , and P, in turn, is the left descendant of its ancestor G. In this case, a tree can be rotated, which changes the roles of the current node N and its ancestor P. Then, for the former parent node P in the updated structure we use case 5, because Property 4 (Both descendants of any red node are black) is still broken. Rotation leads to the fact that some paths (in the subtree marked “1” in the diagram) pass through node N , which was not the case before. This also leads to the fact that some paths (in the subtree marked “3”) do not pass through the node P. However, both of these nodes are red, so Property 5 (All paths from any given node to leaf nodes contain the same number of black nodes) is not impaired by rotation. However, Property 4 is still broken, but now the task is reduced to Case 5. |
void
insert_case4 (struct node * n)
{
struct node * g = grandparent (n);
if ((n == n-> parent-> right) && (n-> parent == g-> left)) {
rotate_left (n-> parent);
/ *
* rotate_left can be performed as follows, considering what is already there * g = grandparent (n)
*
* struct node * saved_p = g-> left, * saved_left_n = n-> left;
* g-> left = n;
* n-> left = saved_p;
* saved_p-> right = saved_left_n;
*
* /
n = n-> left;
} else if ((n == n-> parent-> left) && (n-> parent == g-> right)) {
rotate_right (n-> parent);
/ *
* rotate_right can be performed as follows, considering what is already there * g = grandparent (n)
*
* struct node * saved_p = g-> right, * saved_right_n = n-> right;
* g-> right = n;
* n-> right = saved_p;
* saved_p-> left = saved_right_n;
*
* /
n = n-> right;
}
insert_case5 (n);
}
|
Case 5: P's parent is red, but Uncle U is black, the current node N is the left descendant of P, and P is the left descendant of G. In this case, the tree is rotated by G. The result is a tree in which the former parent P is now the parent of both the current node N and the former grandfather G. It is known that G is black, since its former descendant P could not otherwise be red (without violating Property 4). Then the colors P and G change and as a result the tree satisfies Property 4 (Both descendants of any red node are black). Property 5 (All paths from any given node to leaf nodes contain the same number of black nodes) also remains true, since all paths that pass through any of these three nodes previously passed through G , so now they all pass through P. In each case, of these three nodes, only one is colored black. |
void
insert_case5 (struct node * n)
{
struct node * g = grandparent (n);
n-> parent-> color = BLACK;
g-> color = RED;
if ((n == n-> parent-> left) && (n-> parent == g-> left)) {
rotate_right (g);
} else {/ * (n == n-> parent-> right) && (n-> parent == g-> right) * /
rotate_left (g);
}
}
We will use the notation M for the deleted node; by C we denote the descendant of M , which will also be called simply “his descendant”. If M has a non-leaf descendant, take it as C. Otherwise, for C we take any of the leaf descendants.
If M is a red node, replace it with its descendant C , which by definition must be black. (This can happen only when M has two leaf descendants, because if the red node M has a black non-leaf descendant on one side and on the other hand a leaf, then the number of black nodes on both sides will be different, so the tree will become invalid red-black tree due to violation of Properties 5.) All paths through the node to be deleted will simply contain one red node less, the ancestor and descendant of the node to be deleted must be black, so Property 3 ("All leaves are black") and Property 4 ("Both descendants are beautiful th node - black ") still persists.
Another simple case is when M is black and C is red. Простое удаление чёрного узла нарушит Свойство 4 («Оба потомка красного узла — черные») и Свойство 5 («Всякий простой путь от данного узла до любого листового узла, содержит одинаковое число черных узлов»), но если мы перекрасим С в чёрный, оба эти свойства сохранятся.
Сложным является случай, когда и M и C — черные. (Это может произойти только тогда, когда удаляется чёрный узел, который имеет два листовых потомка, потому что если чёрный узел M имеет чёрного не листового потомка с одной стороны, а с другой — листового, то число черных узлов на обеих сторонах будет различным и дерево станет недействительным красно-чёрным деревом из-за нарушения Свойства 5.) Мы начнем с замены узла M своим потомком C . Будем называть этот потомок (в своем новом положении) N , а его «брата» (другого потомка его нового предка) — S . (До этого S был «братом» M .) На рисунках ниже мы также будем использовать обозначение P для нового предка N (старого предка M ), S L для левого потомка S и S R для правого потомка S ( S не может быть листовым узлом, так как если N по нашему предположению является чёрным, то поддерево P , которое содержит N , чёрной высоты два и поэтому другое поддерево P , которое содержит S должно быть также чёрной высоты два, что не может быть в случае, когда S — лист).
Примечание : В некоторых случаях мы меняем роли и обозначения узлов, но в каждом случае любое обозначение продолжает означать тот же узел, что и в начале случая. Любые цвета, изображенные на рисунке либо предполагаются случаем, либо получается из других предположений. Белый означает неизвестный цвет (либо красный, либо чёрный).
Будем искать «брата», используя эту функцию:
struct node *
sibling(struct node *n)
{
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
Note : In order for a tree to remain truly defined, we need each sheet to remain a sheet after all transformations (so that it has no descendants). If the node we are deleting is not a leaf descendant of N , it is easy to see that the property holds. On the other hand, if the N is a sheet, then, as can be seen from the figures or the code, the property also holds.
We can perform the steps described above using the following code, where the replace_node function puts the child in place of the n node in the tree. For convenience, the code in this section assumes that zero leaves are represented by real node objects, and not NULL (the insert code should work with the same representation).
void
delete_one_child (struct node * n)
{
/ *
* Condition: n has at most one nonzero descendant.
* /
struct node * child = is_leaf (n-> right)? n-> left: n-> right;
replace_node (n, child);
if (n-> color == BLACK) {
if (child-> color == RED)
child-> color = BLACK;
else
delete_case1 (child);
}
free (n);
}
Note : If N is a null sheet and we do not want to represent null sheets as real objects, we can change the algorithm by first calling delete_case1 () on its father (the node we deleted, n in the code above) and deleting it after that. We can do this because the father is black, and therefore behaves like a zero sheet (and sometimes called a 'phantom' sheet). We can safely remove it since n will remain a sheet after all operations, as shown above.
If both N and his current father are black, then deleting the father will cause the paths that pass through N to have one black node less than the paths that do not pass through it. Since this violates property 5 (all paths from any node to its leaf nodes contain the same number of black nodes), the tree must be rebalanced. There are several cases to consider:
Case 1: N is the new root. In this case, everything is done. We have removed one black node from each path and the new root is a black node, so the properties are saved.
void
delete_case1 (struct node * n)
{
if (n-> parent! = NULL)
delete_case2 (n);
}
Note : In cases 2, 5, and 6, we assume that N is the left descendant of its ancestor P. If he is a right descendant, the left and right need to be swapped in all three cases. Again, code samples take this into account.
|
Case 2: S - red. In this case, we change the colors of P and S , and then make a rotation to the left around P , setting S to grandfather N. It should be noted that P must be black if it has a red descendant. Although all paths still contain the same number of black nodes, now N has a black brother and a red father. Thus, we can proceed to step 4, 5 or 6. (His new brother is black because he was a descendant of the red S. ) Next, S will be the new brother N. |
void delete_case2 (struct node * n)
{
struct node * s = sibling (n);
if (s-> color == RED) {
n-> parent-> color = RED;
s-> color = BLACK;
if (n == n-> parent-> left)
rotate_left (n-> parent);
else
rotate_right (n-> parent);
}
delete_case3 (n);
}
|
Case 3: P , S , and children S ' are black. In this case, we simply repaint S to red. As a result, all paths passing through S , but not passing through N , have one less black node. Since the removal of the father N leads to the fact that all the paths passing through N contain one less black node, such actions equalize the balance. However, all paths passing through P now contain one black node less than paths that do not pass through P , therefore property 5 (all paths from any vertex to its leaf nodes contain the same number of black nodes) is still broken. To fix this, we apply the rebalancing procedure to P , starting with case 1. |
void delete_case3 (struct node * n)
{
struct node * s = sibling (n);
if ((n-> parent-> color == BLACK) &&
(s-> color == BLACK) &&
(s-> left-> color == BLACK) &&
(s-> right-> color == BLACK)) {
s-> color = RED;
delete_case1 (n-> parent);
} else
delete_case4 (n);
}
|
Case 4: S and his children are black, but P is red. In this case, we simply change the colors of S and P. This does not affect the number of black nodes on the paths passing through S , but will add one to the number of black nodes on the paths passing through N , thereby restoring the influence of the remote black node. |
void delete_case4 (struct node * n)
{
struct node * s = sibling (n);
if ((n-> parent-> color == RED) &&
(s-> color == BLACK) &&
(s-> left-> color == BLACK) &&
(s-> right-> color == BLACK)) {
s-> color = RED;
n-> parent-> color = BLACK;
} else
delete_case5 (n);
}
|
Case 5: S is black, the left descendant of S is red, the right descendant of S is black, and N is the left descendant of his father. In this case, we rotate the tree to the right around S. Thus the left descendant of S becomes his father and new brother N. After that, we change the colors of S and his new father. All paths still contain the same number of black nodes, but now N has a black brother with a red right descendant, and we go to case 6. Neither N nor his father influence this transformation. (For case 6, we denote by S the new brother N. ) |
void delete_case5 (struct node * n)
{
struct node * s = sibling (n);
if (s-> color == BLACK) {/ * this if statement is trivial,
due to case 2 (even though case 2 changed the sibling to a sibling's child,
since no red parent can have a red child). * /
The following statements should be made:
or right of the right. * /
if ((n == n-> parent-> left) &&
(s-> right-> color == BLACK) &&
(s-> left-> color == RED)) {/ * this last test is trivial too due to cases 2-4. * /
s-> color = RED;
s-> left-> color = BLACK;
rotate_right (s);
} else if ((n == n-> parent-> right) &&
(s-> left-> color == BLACK) &&
(s-> right-> color == RED)) {/ * this last test is trivial too due to cases 2-4. * /
s-> color = RED;
s-> right-> color = BLACK;
rotate_left (s);
}
}
delete_case6 (n);
}
|
Case 6: S is black, the right descendant of S is red, and N is the left descendant of his father P. In this case, we rotate the tree to the left around P , after which S becomes the father of P and his right descendant. Next, we change the colors of P and S , and make the right descendant S black. The subtree still has the same root color, so properties 4 (Both descendants of each red node are black) and 5 (all paths from any vertex to its leaf nodes contain the same number of black nodes) are not violated. However, N now has an additional black ancestor: either P became black, or he was black and S was added as a black grandfather. Thus, the paths passing through the N pass through one additional black node. Meanwhile, if the path does not pass through N , then there are 2 possible options:
In any case, the number of black nodes on these paths will not change. Therefore, we restored properties 4 (Both descendants of each red node are black) and 5 (all paths from any vertex to its leaf nodes contain the same number of black nodes). The white node in the diagram can be either red or black, but should indicate the same color at the beginning and at the end of the transformation. |
void delete_case6 (struct node * n)
{
struct node * s = sibling (n);
s-> color = n-> parent-> color;
n-> parent-> color = BLACK;
if (n == n-> parent-> left) {
s-> right-> color = BLACK;
rotate_left (n-> parent);
} else {
s-> left-> color = BLACK;
rotate_right (n-> parent);
}
}
All recursive function calls are tail and are converted into loops, so the algorithm requires O (1) memory. In the algorithm above, all cases are connected in turn, except for case 3, where a return to case 1, which applies to the ancestor of the node, may occur: this is the only case where a consistent implementation will be an effective cycle (after one rotation in case 3).
Also, tail recursion never occurs on child nodes, so the tail recursion cycle can only move from child nodes to their successive parents. No more than O (log n ) cyclic returns to case 1 will occur (where n is the total number of nodes in the tree before deletion). If in case 2 there is a rotation (the only possible one in the cycle of cases 1-3), then the father of the node N becomes red after rotation and we exit the cycle. In this way, no more than one rotation will be performed during this cycle. After exiting the cycle, no more than two additional turns will occur. But in general, no more than three turns of the tree will occur.
Let the height of the tree be h, the minimum number of vertices is N. Then:
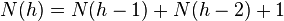. Insofar as 
, 
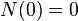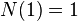, N (h) grows as a Fibonacci sequence, therefore 
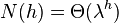where 
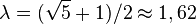
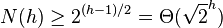
Therefore, with the same number of leaves, a red-ebony tree may be higher than the AVL-tree, but not more than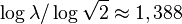 
time. [four]
Since the red-ebony, in the worst case, is higher, the search in it is slower, but the loss in time does not exceed 39%.
The insert requires up to 2 turns in both types of trees. However, due to the greater height of the red-black tree, the insert may take longer.
The AVL-tree in each node stores the height difference (an integer from −1 to +1, 2 bits are needed for coding). A red-ebony tree in each node stores color (1 bit). Thus, a red-black tree can be more economical. (However, if we take into account that in modern computing systems memory is allocated multiple of bytes, then the trees are exactly the same)
However, in practice, in both types of trees, integers are used, since working with bits requires additional processor computations (one assembler command and% al 0x10000000). Nevertheless, there are red-black wood implementations that store the color value in a bit. Example - Boost Multiindex. The purpose of storing color in a bit is to reduce the memory consumption of a red-black tree (Ordered indices node compression). The bit of color in such an implementation is not stored in a separate variable, but in one of the pointers of the tree node (this technique is dangerous to go beyond the limit of available memory).
The red-black tree, which contains n internal nodes, has a height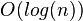 
.
Legend:
- height of the subtree with root in 
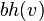- the number of black nodes (not counting 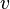if it is black) from 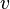to any leaf in the subtree (called black height)Lemma: Subtree with root in node 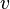has at least 
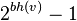internal nodes.
Proof of the lemma (by induction on height):
Base induction: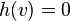 
.
If the subtree has zero height, then 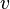should be null , so 
.
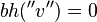So:
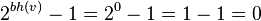
Induction step: let the node 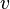such that 
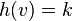and the subtree has at least 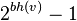internal nodes.
Show that then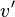 
, for which 
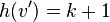has at least 
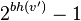internal nodes.
Because 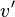It has 
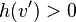This is an internal node. As such, it has two descendants, both of which have a black height. 
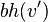either 
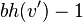(depends on whether 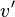red, or black).
By induction hypothesis, each descendant has at least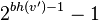 
internal nodes therefore has at least
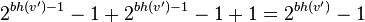
internal nodes.
Using this lemma, we can show that the tree has a logarithmic height. Since at least half of the nodes in any path from the root to the leaf are black (property 4 of the red-ebony tree), the black root height is at least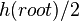 
. By the lemma we have:
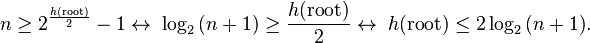
Therefore root height .
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.