Lecture

Due to the specified service discipline, its only position is available on the stack, which is called the TOP of the stack - this is the position in which the last item on the stack is located. When we push a new element onto the stack, it is placed on top of the top and is now at the top of the stack itself. You can select an item only from the top of the stack; at the same time, the selected element is removed from the stack, and at its top is an element that was pushed onto the stack before the selected element (structure with limited access to data). 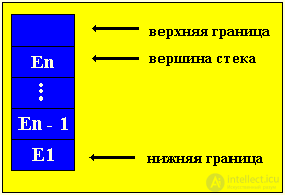
OPERATIONS ON STAGES:
- PUSH (s, i) —the item is pushed onto the stack, where s is the name of the stack, i is the item that is pushed onto the stack;
- POP (s) - selection of an element from the stack. When sampling the element is placed in the working area of memory, where it is used;
- EMPTY (s) - stack checking for emptiness (true - empty, false - non-empty);
- STACKTOP (s) - reading the top element without deleting it.
Fragment of the program to create a stack (the necessary procedures)
Program STACK;
const
max_st = 50;
const
max_st = 50;
var
st, st2: array [1..max_st] of integer;
n: integer;
function empty: boolean; {Check stack for items in it}
begin
empty: = n = 0
end;
procedure push (a: char); {Put item on stack}
begin
inc (n);
st [n]: = a;
end;
procedure pop (var a: char); {Remove item from stack}
begin
a: = st [n];
dec (n);
end;
function full: boolean; {Check for overflow}
begin
Full: = n = max_st
end;
procedure stacktop (var a: char); {Learn top item}
begin
a: = st [n];
end;
begin {Main program}
.
.
end.
Options:
1. Swap the first and last elements of the stack.
2. Expand the stack, i.e. make the bottom of the stack the top and the top the bottom.
3. Remove the element that is in the middle of the stack, if an odd number of elements, and if even, then two medium.
4. Delete every second element of the stack.
5. Insert the '*' character in the middle of the stack, if there is an even number of elements, and if it is odd, then after the middle element.
6. Find the minimum element and insert 0 after it.
7. Find the maximum element and insert 0 after it.
8. Remove the minimum item.
9. Delete all items equal to the first.
10. Delete all items equal to the last.
11.Remove the maximum element.
12. Find the minimum element and insert 0 in its place.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.