Lecture
Objective: to investigate and study search methods with moving to the beginning and transposition.
The task of the work: to master the skills of writing programs for the study of search methods with moving to the beginning and transposition in the programming language PASCAL.
Operating procedure :
SEARCH is one of the foundations of computer data processing. Its purpose is to, based on a given argument, find among the data array that data that corresponds to this argument or determine that this data is not. If this data is not available, add it to the data array.
Any data set will be called TABLE or FILE. This or a structure element differs in some way from other data. This feature is called KEY. The key can be UNIQUE, i.e. there is only one data in the table with such a key, otherwise the unique keys are called PRIMARY KEYS.
SECONDARY KEY in one table can be repeated, but it is also possible to organize a search by it. Data keys are collected in one place (table).
Keys that are allocated from a data table and organized into their own file are called EXTERNAL KEYS. If the key is in the record, then it is called the INNER KEY.
SEARCH BY SPECIFIED ARGUMENT is an algorithm that determines the correspondence of a given key with a given argument. The result of the search algorithm may be finding this data or the absence of data in the table. In the absence of this, two operations are possible:
1. Indication that this is not.
2. Insert this into the table.
Let K be an array of keys, then for all K (i) there is R (i) - given. KEY is a search argument. It corresponds to the information record REC. Depending on the data structure in the table, there are several types of search.
ORDERING SEARCH TABLE
You can always talk about a certain value of the probability of finding an element.
P (i) is the probability of finding an element.
In this case, the lookup table is represented as a system with discrete states, and the sought-for element is characterized by the i-th state of the system, the probability of which is P (i).
P (1) + P (2) + ... + P (n) = 1
The number of Z comparisons when searching in the table, i.e. The number of comparisons needed to search for a given argument is the value of a discrete random variable determined by the numbers of states and the probabilities of the states of the system.
Z = 1 * P (1) + 2 * P (2) + 3 * P (3) + ... + n * P (n)
DATA TABLE MUST BE ORDERED SO, so that at the beginning of the table there are items with high search probabilities or items that are most often addressed in the table.
P (1)> = P (2)> = P (3)> = ...> = P (n)
There are two main methods for reordering search tables:
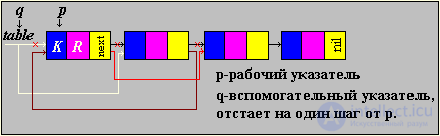
The found element is immediately in the head of the list.
Initially, the q pointer is zero, the p pointer points to the beginning of the list; p moves to the second element, and q moves to the first. The pointer to the beginning of the list (table) is moved to the second element, and the pointer to the second element to the third. Thus the second element moves to the first place.
(Pseudocode)
q = nil
p = table
WHILE (p <> nil) do
IF key = k (p)
then SEARCH = p
next (q) = next (p)
next (p) = q
table = p
return
end IF
q = p
p = next (p)
end WHILE
SEARCH = 0
return
In this method, the found element is rearranged by one element to the head of the list. If this element is addressed frequently, then gradually moving to the top of the list, it will soon be in his head.
This method is convenient in that it is effective not only in list structures, but also in unordered arrays, since only two adjacent elements are swapped.
We will use three pointers:
p - working pointer points to the element.
q - auxiliary pointer, one step behind p.
s - auxiliary pointer, two steps behind p. 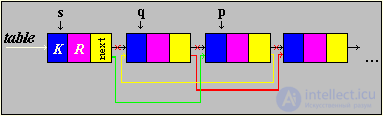
The third element found by us moves one step to the head of the list (that is, it becomes the second). The pointer of the first element moves to the third element, the pointer of the second element to the fourth, thus the third element moves to second place. If this element is addressed again, it will be in the head of the list.
s = nil
q = nil
p = nil
while (p <> nil) do
if key = k (p) then search = p
if q = nil then return
else next (q) = next (p)
next (p) = q
if s = nil then table
else next (s) = p
end if
search = p
end if
end if
return
end while
search = nil return
An array of integers is given. Create procedures for the method of transposition and rearrangement in the beginning. Solve the given problem and rearrange the element found in the problem using both methods to the top of the list.
OPTION 1. Find the maximum element of the array.
OPTION 2. Find the minimum element of the array.
OPTION 3. Find the number that is divisible by 11 (if there are several such numbers, then find the maximum; if there are no such numbers, give a message).
OPTION 4. Find the number that is divisible by 11 (if there are several such numbers, then find the maximum; if there are no such numbers, give a message).
OPTION 5. Find an element whose difference in neighboring elements is at least 72. If there are several such elements, select the maximum one. If there are no such elements, issue a message.
OPTION 6. Find an element whose quotient of neighboring elements is an even number. If there are several such elements, select the maximum or minimum element. If there are no such elements, issue a message.
OPTION 7. Find the element whose difference in neighboring elements is an even number. If there are several such elements, select the maximum or minimum element. If there is no such item, issue a message.
OPTION 8. Find the element, the arithmetic average of the elements that are before this element is 12. If there are no such elements, give a message.
OPTION 9. Find the maximum element divisible by 10. If there is no such element, display a message.
OPTION 10. Find an element whose difference in neighboring elements is an even number and is divisible by 3. If there is no such element, display a message.
OPTION 11. Find the element, the mean square of the elements that are after this element is less than 10. If there are several such elements, select the maximum element. If there are no such elements, issue a message.
OPTION 12. Find the value of tg (x) from each element and rearrange to 1 place the element, the value of which is the maximum.
Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.