2-3 tree

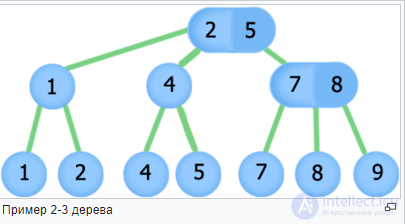
Example 2-3 tree

2-3 tree (Eng. 2-3 tree ) - a data structure that is a balanced search tree, such that two or three branches can go out of each node and the depth of all leaves is the same. It is a special case of B + tree .

Properties

2-3 tree - a balanced search tree with the following properties:

• non-leaf vertices have either or sons,
• the leafy top with two sons holds the maximum left subtree. A leafy peak with three sons holds two values. The first value stores the maximum of the left subtree, the second maximum of the central subtree,
• sons are ordered by the maximum value of the subtree of the son,
• all the leaves are at the same depth
• height of 2-3 trees , where - the number of elements in the tree.

Operations

We introduce the following notation:

• - the root of 2-3 trees.

Each tree node has fields:

• - the parent of the node,
• - sons of the knot,
• - keys of the node,
• - the number of sons.

Search

• - the desired value,
• - the current vertex in the tree.

Initially, . We will look at the keys in the nodes until the node is a leaf. Consider two cases:

• the current peak has two sons. If its value is less than , then , otherwise .

• the current peak has three sons. If the second value is less than , then . If the first value is less than , then , otherwise .

  T search ( T x):
   Node t = root
   while (t is not a leaf)
     if (t.length == 2)
       if (t.keys [0] else 
         t = t.sons [0]
     else if (t.keys [1] else if (t.keys [0] else 
       t = t.sons [0]
   return t.keys [0]

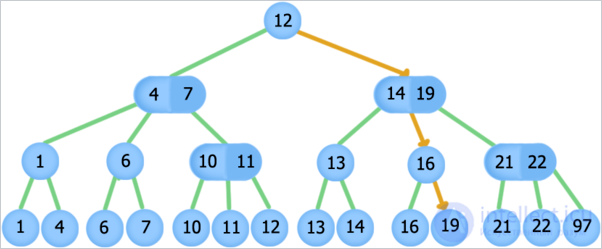
Search for element 19, orange arrows indicate the path through the tree when searching

Insert item

• - added value,
• - the current vertex in the tree. Initially, .

If the root does not exist - the tree is empty, then the new element will be the root (at the same time as the leaf). Otherwise, proceed as follows:

First, find where the element would be by applying . Next, check if this node has a parent, if it does not, then there is only one element in the tree - the sheet. Take this sheet and the new node, and create a parent for them, arrange the sheet and new node in ascending order.

If the parent exists, then we will hang another son to it. If the sons became , then we divide the parent into two nodes, and repeat the separation now for his parent, because he also could already have sons, and we divided him became son more. (before dividing, we will update the keys).

  function splitParent ( Node t):
  if (t.length> 3) 
    Node a = Node (sons = {t.sons [2], t.sons [3]}, keys = {t.keys [2]}, parent = t.parent, length = 2)
    t.sons [2] .parent = a
    t.sons [3] .parent = a
    t.length = 2
    t.sons [2] = null
    t.sons [3] = null
    if (t.parent! = null )
      t.parent [t.length] = a
      t.length ++
      sort sons at t.parent
      splitParent (t.parent)
    else // we split the root, we need to suspend it to the common parent, which will be the new root
     Node t = root
     root.sons [0] = t
     root.sons [1] = a
     t.parent = root
     a.parent = root
     root.length = 2
     sort sons at root

If the sons became , then we do nothing. Next, you need to restore the keys on the way from the new top to the root:

  function updateKeys ( Node t): 
   Node a = t.parent
   while (a! = null )
    for i = 0 .. a.length - 1
      a.keys [i] = max (a.sons [i]) // max - returns the maximum value in the subtree.
    a = a.parent // Note: max is easy to find if you store the maximum
                                 // right subtree in each node - this is the value and will be max (a.sons [i])

must be run from a new node. Adding an item:

  function insert ( T x):
   Node n = Node (x)
   if (root == null ) 
    root = n
    return
   Node a = searchNode (x)     
   if (a.parent == null ) 
     Node t = root
     root.sons [0] = t
     root.sons [1] = n
     t.parent = root
     n.parent = root
     root.length = 2
     sort sons at root
   else 
     Node p = a.parent
     p.sons [p.length] = n
     p.length ++
     n.parent = p
     sort s s u p
     updateKeys (n) 
     split (n)
   updateKeys (n) 

Since we go down once and go up when we split our parents no more than once, works for .

Examples of adding:

Adding item with key 6

Delete item

• - value of the deleted node,
• - current node,
• - brother ,
• - father ,
• - the neighboring brother ,
• - father .

Let initially be the node where .

If does not have a parent, then this is the root (at the same time, it is the only element in the tree). Let's remove it.

If exists, and he has strictly more than sons, then simply remove , and reduce number children.

If the parent two sons, we will consider possible cases (first we delete everywhere:)

• does not exist, then we remove one of the sons of the root, therefore, the other son becomes the new root,
• had sons, had sons. We hook to and delete . Since - the parent of , also had two sons, we repeat the same reasoning for ,
• had or sons, had sons. Just take the son closest to us from and attach it to . Let's restore order in the sons . Now again had two sons and all nodes of 2-3 trees are correct,
• had sons, had sons. We hang to and delete , and for reduce the number of children. Since had three sons, and still has more than one son, all nodes 2-3 of the tree are correct.

We generalize the algorithm when deleting when the parent two sons:

• If does not exist, then it turns out that we are now removing some of the sons of the root (for definiteness, further left, with the right similar). Then now the right son becomes the root. This ends the removal.

• If exists, then delete , and his brother ( ) will be hooked to . Now could have sons, so we repeat the same steps from : call and . Now recursively delete .

As a result, we get a 2-3 tree that is correct in structure, but we have a violation in the keys in the nodes, fix them using , starting from .

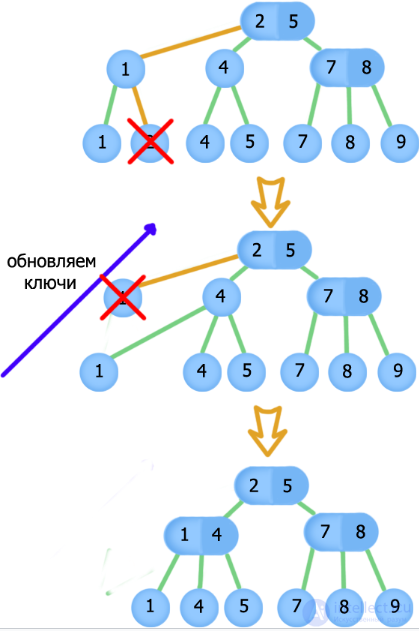
Delete item with key 2

Next and previous

• - search parameter,
• - current node.

Due to the fact that our nodes are sorted to the maximum in the subtree, the next object is the neighboring sheet on the right. You can get there as follows: we will go up until we have the first opportunity to turn right down. As soon as we turn right down, we will always go left. Thus, we will appear in the next sheet. If we have never been able to turn right down and come to the root, then the next object does not exist. The case with the previous is symmetric.

  T next ( T x):
    Node t = searchNode (x)
    if (t.keys [0]> x) // x was not in the tree, and we found the next one right away
      return t.keys [0]
    while (t! = null )
      t = t.parent
      if (can be turned right down)
       at t we place the vertex into which we turned
       while (while t is not a leaf)
        t = t.sons [0]
      return t
    return t.keys [0]
    

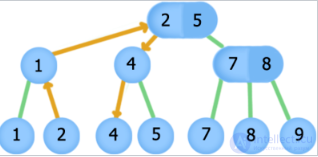
Path when searching for the next item after 2

Finding m of the following items

B + trees, support the operation , which allows you to find m of the following elements. The naive implementation is as follows: we will call times to search for the next element, this solution works for . But 2-3 trees allow finding the next m elements behind , which greatly speeds up the search for large . By construction, all the leaves are sorted in ascending order, we will use this to find m elements. We need to connect the leaves, for this we modify and . Add the following fields to the nodes:

• - points to the right sheet,
• - points to the left sheet.

Let be the added node. Change as follows: at the very end, after we have updated all the keys, we will find and write a link to it at . Similarly with the left.

Let be the node to be deleted. Change as follows: at the very beginning, before deleting , we will find the next and write it in right sheet relative to . With the left we will do the same.

As a result, we have a doubly connected list in the leaves, and in order to display elements, we just need to find the necessary element once and go right to the elements.

See also

• B-tree
• Splay tree
• AVL tree
• Cartesian tree
• Red ebony