Lecture
| Persistent data structures ( persistent data structure ) are data structures that, when they make any changes, retain all of their previous states and access to these states. |
There are several levels of persistence:
In partly persistent data structures, queries can be made to each version, but only the latest version of the data structure can be modified.
In fully persistent data structures, you can change not only the latest, but also any version of data structures, and you can also make queries to any version.
Confluent data structures allow you to combine two data structures into one (search trees that can be merged).
Functional data structures are completely persistent by definition, since they suppress destroying assignments, i.e. Any variable value can be assigned only once and you can not change the values of variables. If the data structure is functional, then it is confluent, if confluent, then completely persistent, if completely persistent, then partially persistent. However, data structures are not functional, but confluent.
There are several ways to make any structure persistent:
Consider to begin with a partial persistence. For clarity, we number different versions of data structures. The history of data structure changes is linear, at any time you can refer to any version of the data structure, but only the latest version can be changed (in the figure it is highlighted in blue).

We formulate what the data structure. In our understanding, the data structure will be the set of nodes in which some data is stored, and these nodes are linked by links. An example of a data structure is a tree. Consider how to copy a path into a persistent tree by copying the path.
Let there be a balanced search tree. All operations in it are done for 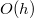 where
where 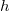 - tree height and tree height
- tree height and tree height 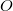
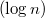 where
where 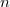 - the number of vertices. Suppose you need to make some kind of update in this balanced tree, for example, add another element, but you do not need to lose the old tree. Take the node in which to add a new child. Instead of adding a new child, copy this node, add a new child to the copy, also copy all nodes up to the root, from which the first copied node is reachable along with all pointers. All vertices from which the modified node is not reachable, we do not touch. The number of new nodes will always be of the order of the logarithm. As a result, we have access to both versions of the tree.
- the number of vertices. Suppose you need to make some kind of update in this balanced tree, for example, add another element, but you do not need to lose the old tree. Take the node in which to add a new child. Instead of adding a new child, copy this node, add a new child to the copy, also copy all nodes up to the root, from which the first copied node is reachable along with all pointers. All vertices from which the modified node is not reachable, we do not touch. The number of new nodes will always be of the order of the logarithm. As a result, we have access to both versions of the tree.
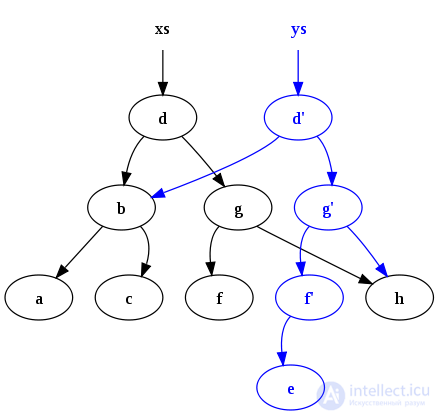
Since a balanced search tree is considered, lifting the top up while balancing, you need to make copies of all the vertices participating in the rotations, which have changed the links to the children. There are always no more than three, so the asymptotics 
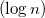 will not suffer. When balancing is over, you need to go up to the root, making copies of the vertices on the way.
will not suffer. When balancing is over, you need to go up to the root, making copies of the vertices on the way.
This method works well on stack, binary (Cartesian, red-black) trees. But in the case of transforming a queue into a persistent add operation, it will be very expensive, since the element is added to the tail of the queue, which is reachable from all other elements. It is also not beneficial to use this method in the case when the data structure contains references to the parent.
Implementation based on the segment tree
Based on the segment tree, you can build a fully persistent data structure.
To implement a persistent segment tree, it is convenient to change the tree structure somewhat. For this we will use explicit pointers. 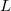 and
and 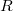 for children. In addition, we will get an array
for children. In addition, we will get an array 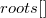 , wherein
, wherein 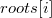 points to the root of the line segment tree
points to the root of the line segment tree 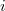
To build a persistent tree of segments of 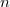 elements need to apply
elements need to apply 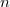 operation to add an item to the latest version of the tree. To add a new item to
operation to add an item to the latest version of the tree. To add a new item to 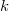 version of the tree, you need to check whether it is full binary. If yes, then create a new root, make the left son
version of the tree, you need to check whether it is full binary. If yes, then create a new root, make the left son 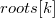 . Otherwise, make a copy of the root of the original version. Add the root to the end of the root array. Next, going down from the root to the first free sheet, we will create non-existent nodes and clone the existing ones. After that, in the new branch, it is necessary to update the function value and some pointers of child elements. Therefore, returning from recursion, we will change one pointer to the newly created or copied vertex, and also update the value of the function for which the tree was built. After this operation, a new version will appear in the tree containing the inserted element.
. Otherwise, make a copy of the root of the original version. Add the root to the end of the root array. Next, going down from the root to the first free sheet, we will create non-existent nodes and clone the existing ones. After that, in the new branch, it is necessary to update the function value and some pointers of child elements. Therefore, returning from recursion, we will change one pointer to the newly created or copied vertex, and also update the value of the function for which the tree was built. After this operation, a new version will appear in the tree containing the inserted element.
In order to change an element in a persistent segment tree, you need to do the following: go down in the tree from the root of the required version to the required element, copy it, change the value, and, climbing up the tree, we will clone the nodes. At the same time, it is necessary to change the pointer to one of the children for the node created during the previous cloning. After copying the root, add a new root to the end of the root array.
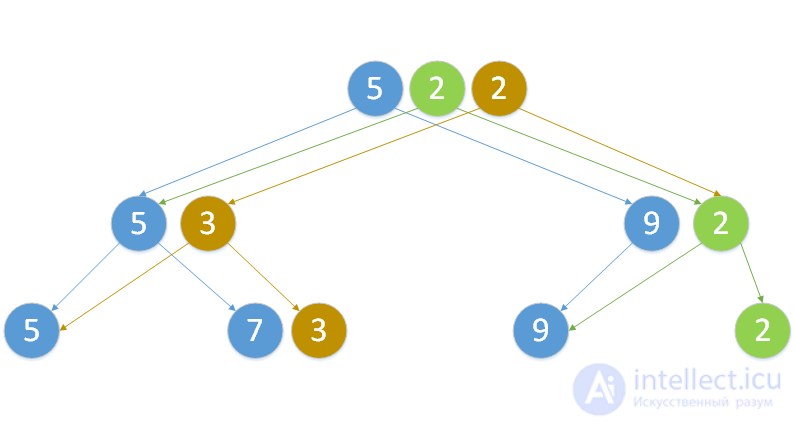
Here you can see a persistent segment tree with a minimum operation, in which initially there were 3 vertices. First, a vertex with a value of 2 was added to it, and then a vertex was changed with a value of 7. The color of the edges and vertices corresponds to the time of their appearance. The blue color of the elements means that they were originally, green - that they appeared after adding, and orange - that they appeared after changing the element.
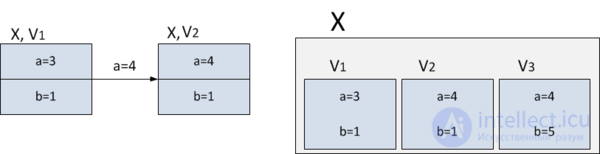
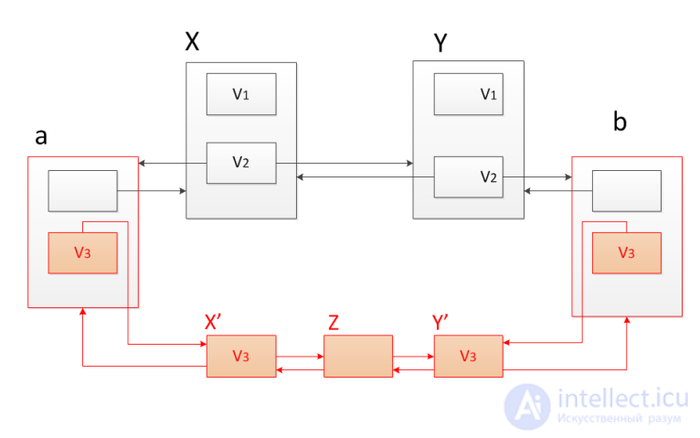
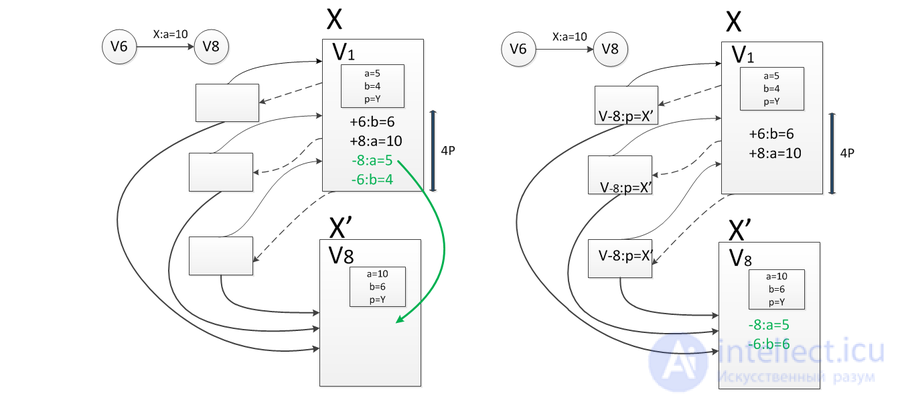
Suppose there is a node in the data structure in which changes need to be made (for example, in the figure below in the first version of the data structure in the node  there is a field
there is a field 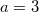 and in the second version this field should be equal to
and in the second version this field should be equal to 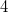 ), but you still need to keep access to the old version of the node
), but you still need to keep access to the old version of the node  and do not need to save time. In this case, both versions of the node can be stored.
and do not need to save time. In this case, both versions of the node can be stored.  in a large combo box.
in a large combo box.
Go
In the example above, the first version will be stored in this “fat” node. 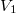 , in which
, in which 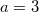 and the second version
and the second version 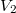 , in which
, in which 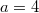 . If any further changes follow (for example, the field
. If any further changes follow (for example, the field 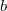 node
node  will be equal to
will be equal to 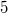 ) add to the thick knot
) add to the thick knot  one more version -
one more version - 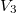 .
.
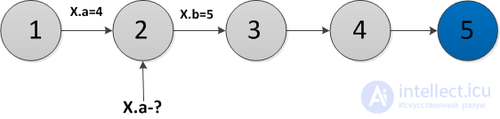
Suppose you need to make a request to the second version of the data structure (in the figure above this is the request 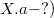 . To make this request, you need to go to the node
. To make this request, you need to go to the node  and find in the list of versions the maximum version that is less than or equal to the version of the request (in the example in the figure this is the version
and find in the list of versions the maximum version that is less than or equal to the version of the request (in the example in the figure this is the version 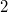 ), and in this version of the node to find the value of the field
), and in this version of the node to find the value of the field  (in the example
(in the example 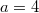 ). To quickly find the version you need in the list of versions stored in the thick node, you need to store them in a tree. Then we will be able to find the necessary version for the logarithm and refer to it. This means that all operations that will be performed on this data structure will be multiplied by the logarithm of the number of versions.
). To quickly find the version you need in the list of versions stored in the thick node, you need to store them in a tree. Then we will be able to find the necessary version for the logarithm and refer to it. This means that all operations that will be performed on this data structure will be multiplied by the logarithm of the number of versions.
The structure of a thick node may be different: for each vertex, you can store a log of its changes, in which the version in which the change occurred is recorded, as well as the change itself. Such a structure of a thick node is discussed below, in the sections on general methods for obtaining partially and fully persistent data structures. The log can be organized in different ways. Usually make a separate log for each field vertices. When something changes at the vertex, then the change and the version number with which the change occurred is recorded in the log of the corresponding field. When you need to access the old version, then a binary search searches the log for the latest change to this version and finds the desired value. Fat node method gives a slowdown 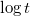 where
where 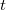 - the number of changes in the data structure; memory required
- the number of changes in the data structure; memory required 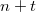 where
where 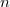 - the number of vertices in the data structure.
- the number of vertices in the data structure.
If we combine the path copiyng and fat node methods, we obtain a universal method that will allow transforming data structures into partially persistent without additional logarithm of memory and time. Suppose we have a doubly linked list and want to make some change to it, for example, add a node 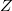 between nodes
between nodes  and
and 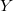 that is, when moving from version
that is, when moving from version 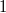 in version
in version 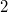 add a node to the doubly linked list
add a node to the doubly linked list 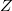 . Apply the "thick" nodes method. To do this in nodes
. Apply the "thick" nodes method. To do this in nodes  and
and 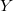 add the second version and change the link following from
add the second version and change the link following from  and the previous one before
and the previous one before 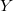 , as it shown on the picture. This algorithm works as follows. For example, the current first version. Go through the list from left to right from the first node to the node
, as it shown on the picture. This algorithm works as follows. For example, the current first version. Go through the list from left to right from the first node to the node  and then go to the next node. In the "thick" node
and then go to the next node. In the "thick" node  Select the desired (first) version and then follow the links.
Select the desired (first) version and then follow the links.
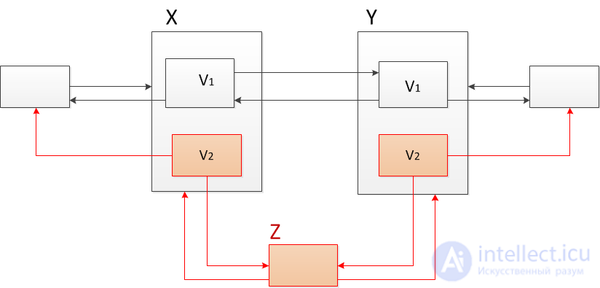
Suppose we want to add another element between the nodes  and
and 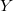 but the problem is that
but the problem is that  and
and 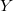 there is already a second version, if we add more new versions, we will get an additional logarithm of time when accessing the node, as in the “thick” nodes method discussed above. Therefore, we will not add more than two versions. Use the copy path method. Copy the nodes
there is already a second version, if we add more new versions, we will get an additional logarithm of time when accessing the node, as in the “thick” nodes method discussed above. Therefore, we will not add more than two versions. Use the copy path method. Copy the nodes  and
and 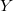 , starting with their third version, and associate the new nodes with the original list. To do this, add the second version of the previous one before
, starting with their third version, and associate the new nodes with the original list. To do this, add the second version of the previous one before  and subsequent after
and subsequent after 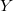 nodes and link these nodes with corresponding links. So all versions remain available.
nodes and link these nodes with corresponding links. So all versions remain available.
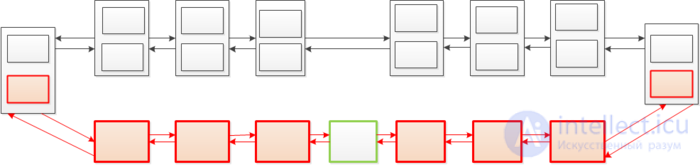
We will call a node complete if it has a second version. If we want to insert a new element in the middle of the list (in the figure below it is marked in green), we must clone all the full nodes to the left and right of the place where the new node is added, reach the nearest elements that do not have the second version and add the second version.
Let us estimate the depreciation time of such an algorithm. We have a partially persistent data structure, you can only change its latest version. Take the potential function 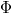 equal to the number of full nodes in the latest version.
equal to the number of full nodes in the latest version.
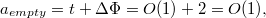 as if adding a node does not affect full nodes, then a node is added in constant time, and the number of full nodes increases by
as if adding a node does not affect full nodes, then a node is added in constant time, and the number of full nodes increases by 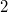 .
.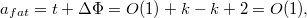 since if a node entails changes to full nodes, it will be spent first
since if a node entails changes to full nodes, it will be spent first 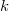 time to copy these full nodes, and at the same time, the potential will decrease by
time to copy these full nodes, and at the same time, the potential will decrease by 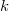 and then the maximum will increase by
and then the maximum will increase by 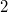 .
.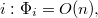 since the total nodes are not larger than the total number of nodes in the list.
since the total nodes are not larger than the total number of nodes in the list.Thus, according to the theorem on the method of potentials, the depreciation time of work on adding an element will be 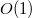 .
.
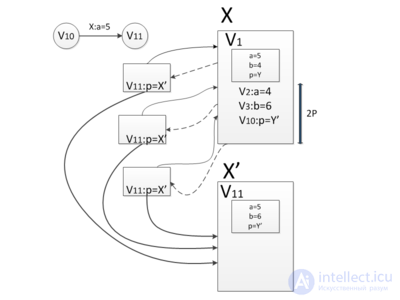
Dotted lines - backlinks,
 - source node, up to version
- source node, up to version 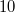 ,
,
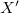 - cloned assembly, current from version
- cloned assembly, current from version 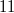 , with an empty list of changes
, with an empty list of changes
We apply the methods described above to the abstract data structure in general.
Let there be a data structure, each node has a number of pointers to this node no more than some constant 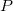 . When cloning a node, it is important to know where the signs come from to that node in order to rearrange them. Therefore, it is necessary in each node to keep backlinks to those nodes that refer to the cloned node. All nodes will be stored as “thick” nodes, which contain the initial version of this node and a list of changes made to it (eng. Change log ) of a length not exceeding
. When cloning a node, it is important to know where the signs come from to that node in order to rearrange them. Therefore, it is necessary in each node to keep backlinks to those nodes that refer to the cloned node. All nodes will be stored as “thick” nodes, which contain the initial version of this node and a list of changes made to it (eng. Change log ) of a length not exceeding 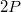 .
.
Suppose you need to make a change in the data structure of the node  . If there is a place in the list of changes, we simply make a change there: we write the version number with which the change begins, to which field of the node the change is made and which one. If change log is full, then clone the node
. If there is a place in the list of changes, we simply make a change there: we write the version number with which the change begins, to which field of the node the change is made and which one. If change log is full, then clone the node  : we take the starting version of the node, make all the changes recorded in the change log , add the last change and make a version with a free list of changes. Then follow the back links from
: we take the starting version of the node, make all the changes recorded in the change log , add the last change and make a version with a free list of changes. Then follow the back links from  and in the change log of each node that references
and in the change log of each node that references  , add a pointer change starting from this version of the data structure with
, add a pointer change starting from this version of the data structure with  on
on 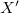 .
.
We estimate the running time of this algorithm. We introduce a potential function that will be equal to the total size of all change lists in the latest version. Let's see how the total size of change lists changes when we make one change. If the change log was not complete, then we simply add one element there, the potential will increase by one. If the change log was full, then the potential is reduced by its size, since we have cloned a node with an empty list of changes. After that we went back links (they were 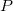 pieces) and added to the
pieces) and added to the 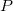 nodes by one value. Thus, the amortized running time will be
nodes by one value. Thus, the amortized running time will be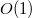 .
.
For fully persistent data structures, the conversion method described above will not work, since the version creation history is not linear and you cannot sort changes by version, as in partially persistent data structures. Let us store the history of version changes in the form of a tree. Let's go around this tree in depth. In order of this detour we will write down when we enter, and when we exit each version. This sequence of actions completely sets the tree; we make a list of it. When after some version (in the figure below it is a version 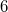 ) a new version of the data structure is added (in the figure version
) a new version of the data structure is added (in the figure version 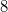 ), we insert two items into the list (in the figure this is
), we insert two items into the list (in the figure this is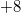 and
and 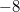 ) after logging in, but before exiting the version when the change occurred (that is, between the elements
) after logging in, but before exiting the version when the change occurred (that is, between the elements 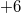 and
and 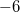 ).The first element makes a change, and the second will return the value of the previous version. Thus, each operation is divided into two: the first makes a change, and the second rolls it back.
).The first element makes a change, and the second will return the value of the previous version. Thus, each operation is divided into two: the first makes a change, and the second rolls it back.
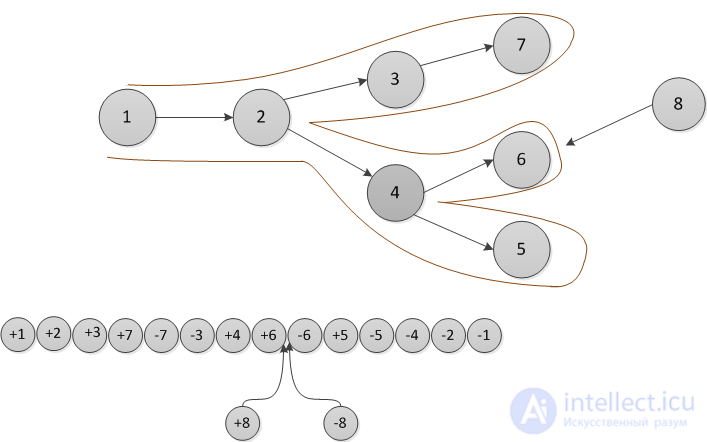
To implement the method of converting data structures to fully persistent, described in the previous paragraph, we need a list that supports operations 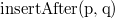 (insert
(insert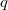 after
after 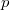 ) and
) and 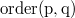 (should be able to respond to requests of the form "
(should be able to respond to requests of the form " 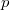 lies in this list before
lies in this list before 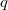 ").
"). 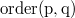 returns
returns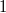 , if a
, if a 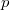 lies up
lies up 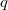 and
and 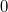 otherwise. This is a list with the support of the Order Order List Order Maintenance , which does both of these operations for
otherwise. This is a list with the support of the Order Order List Order Maintenance , which does both of these operations for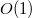 .
.
В change log «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут добавляться в change log не по номерам версий, а по их порядку в списке версий List Order Maintenance .
Когда есть запрос к какой-то версии, то нужно найти в списке версий такую, после входа в которую, но до выхода из которой лежит версия запроса, а среди таких максимальную. Например, если приходит запрос к версии 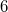 на рисунке выше, то мы видим, что она в списке версий лежит после входа, но до выхода в версии
на рисунке выше, то мы видим, что она в списке версий лежит после входа, но до выхода в версии 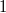 ,
, 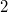 and
and 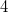 . Необходимо найти наибольшую из них. Список List Order Maintenance позволяет делать это за
. Необходимо найти наибольшую из них. Список List Order Maintenance позволяет делать это за 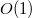 с помощью операции
с помощью операции 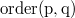 . In the example, this is the version
. In the example, this is the version 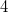 .Since the change log of each node has a constant size, the search for the required version in it occurs for
.Since the change log of each node has a constant size, the search for the required version in it occurs for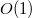 .
.
At some point, the change log of the thick node will overflow. Then you need to clone this node and transfer the lower half of the changes to the change log of the cloned node. We apply the first half of the changes to the original version of the node and save it as the initial version in the cloned node.
There will be two nodes: the first is responsible for the segment of versions before the last modification operation, and the second - after it. The further procedure is similar to that used in the general method of constructing partially persistent data structures.
Оценим амортизационное время работы этого алгоритма. Введем функцию потенциала, равную числу полных узлов. Когда узел раздваивается, функция потенциала уменьшается на единицу, затем мы переставляем  ссылок, потенциал увеличивается на
ссылок, потенциал увеличивается на  , значит, амортизационное время работы —
, значит, амортизационное время работы —  .
.
Persistent data structures are used in solving geometric problems. An example is the Point location problem - the problem of the location of the point. Tasks of this kind are solved offline and online . In offline tasks all requests are given in advance and you can process them simultaneously. In online tasks, the next request can be found only after finding the answer to the previous one.
При решении offline -задачи данный планарный граф разбивается на полосы вертикальными прямыми, проходящими через вершины многоугольников. Затем в этих полосах при помощи техники заметающей прямой (scane line) ищется местоположение точки-запроса. При переходе из одной полосы в другую изменяется сбалансированное дерево поиска. Если использовать частично персистентную структуру данных, то для каждой полосы будет своя версия дерева и сохранится возможность делать к ней запросы. Тогда Point location problem может быть решена в online .
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL