Lecture
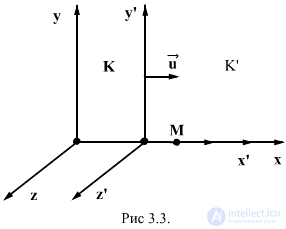
Consider two reference systems: fixed (K) and moving relative to the first along the X axis with a constant X with a constant speed 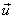 (K '). The coordinates of the body M in the system K x: y: z, and in the system K '- x': y ': z'. These coordinates are related to each other by the relations that are called the Galilean transformation
(K '). The coordinates of the body M in the system K x: y: z, and in the system K '- x': y ': z'. These coordinates are related to each other by the relations that are called the Galilean transformation
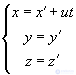
Differentiating these equations over time and considering that 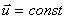 , we find the relationship between speeds and accelerations:
, we find the relationship between speeds and accelerations:
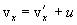 | 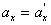 |
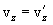 | 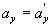 |
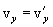 | 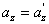 |
Thus, if in system K a body has an acceleration a, then it has the same acceleration in system K '.
According to Newton's second law:
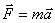
those. Newton's second law is the same in both cases.
With 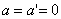 motion by inertia, thus, the Newton's first law is also valid, i.e. the mobile system under consideration is inertial. Consequently, Newton's equations for the material point, as well as for an arbitrary system of material points are the same in all inertial reference systems - invariant with respect to the Galilean transformations. This result is called the mechanical principle of relativity (Galilean principle of relativity), and is formulated as follows: uniform and straight-line movement (relative to any inertial reference system) of a closed system does not affect the patterns of mechanical processes in it. Consequently, in mechanics all inertial reference systems are completely equal. Therefore, no mechanical experiments inside the system can detect whether the system moves evenly and rectilinearly or is at rest.
motion by inertia, thus, the Newton's first law is also valid, i.e. the mobile system under consideration is inertial. Consequently, Newton's equations for the material point, as well as for an arbitrary system of material points are the same in all inertial reference systems - invariant with respect to the Galilean transformations. This result is called the mechanical principle of relativity (Galilean principle of relativity), and is formulated as follows: uniform and straight-line movement (relative to any inertial reference system) of a closed system does not affect the patterns of mechanical processes in it. Consequently, in mechanics all inertial reference systems are completely equal. Therefore, no mechanical experiments inside the system can detect whether the system moves evenly and rectilinearly or is at rest.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics