Lecture
Curvilinear motion is a motion whose trajectory is a curved line (for example, a circle, ellipse, hyperbola, parabola). An example of curvilinear motion is the movement of the planets, the end of the clock hand on the dial, etc. In the general case, the speed during curvilinear motion varies in magnitude and direction.
Curvilinear motion of a material point is considered uniform motion if the velocity modulus is constant (for example, uniform motion along a circle), and uniformly accelerated if the modulus and direction of velocity changes (for example, the motion of a body thrown at an angle to the horizon).
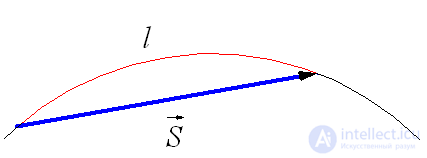
When moving along a curved path, the displacement vector 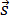 sent along the chord (Fig. 1.19), and l - the length of the trajectory. The instantaneous velocity of the body (that is, the velocity of the body at a given point of the trajectory) is tangential at the point of the trajectory where the moving body is at a given moment (Fig. 1.20).
sent along the chord (Fig. 1.19), and l - the length of the trajectory. The instantaneous velocity of the body (that is, the velocity of the body at a given point of the trajectory) is tangential at the point of the trajectory where the moving body is at a given moment (Fig. 1.20).
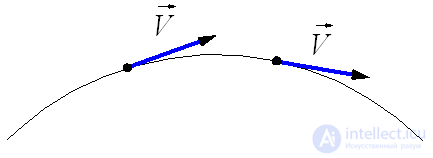
Curvilinear motion is always accelerated motion. That is, acceleration during curvilinear motion is always present, even if the velocity modulus does not change, only the direction of velocity changes. The change in the magnitude of velocity per unit of time is tangential acceleration:
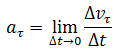
or 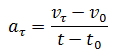
Where v τ , v 0 - values of speeds at the moment of time t 0 + Δt and t 0, respectively.
Tangential acceleration at a given point of the trajectory in the direction coincides with the direction of the velocity of the body or opposite to it.
Normal acceleration is the change in speed in a direction per unit of time:
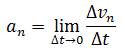
Normal acceleration is directed along the radius of curvature of the trajectory (to the axis of rotation). Normal acceleration perpendicular to the direction of speed.
Centripetal acceleration is normal acceleration with uniform motion in a circle.
Full acceleration with a uniformly curved body motion is equal to:
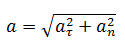
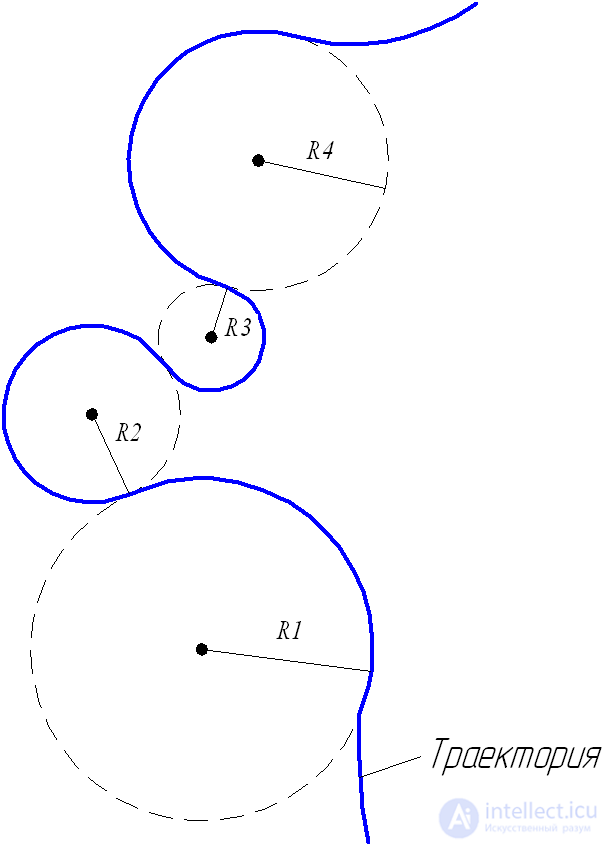
The movement of the body along a curvilinear trajectory can be approximated as a movement along the arcs of certain circles (Fig. 1.21).
In the case of rectilinear motion, the vectors of speed and acceleration coincide with the direction of the trajectory. Consider the motion of a material point along a curved plane trajectory. The velocity vector at any point of the trajectory is tangential to it. Assume that in the TM trajectory the speed was 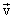 , and in M. 1 became
, and in M. 1 became  . At the same time, we consider that the time span when a point passes on the path
. At the same time, we consider that the time span when a point passes on the path 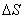 from M to M 1 is so small that the change in acceleration in magnitude and direction can be neglected. To find the velocity change vector
from M to M 1 is so small that the change in acceleration in magnitude and direction can be neglected. To find the velocity change vector 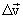 It is necessary to determine the vector difference:
It is necessary to determine the vector difference:
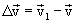
For this we will transfer  parallel to itself, combining its beginning with point M. The difference of two vectors is equal to the vector connecting their ends
parallel to itself, combining its beginning with point M. The difference of two vectors is equal to the vector connecting their ends 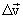 equal to the side of the speaker
equal to the side of the speaker  MAC, built on the velocity vectors, as on the sides. Expand the vector
MAC, built on the velocity vectors, as on the sides. Expand the vector 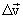 into two components AB and AD, and both respectively
into two components AB and AD, and both respectively  and
and 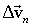 . Thus, the velocity change vector
. Thus, the velocity change vector 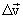 equal to the vector sum of two vectors:
equal to the vector sum of two vectors:
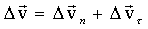
By definition:
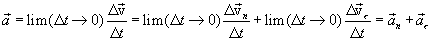 | (1.15) |
Tangential acceleration 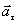 characterizes the rapidity of change in the speed of movement by the numerical value and is directed tangentially to the trajectory.
characterizes the rapidity of change in the speed of movement by the numerical value and is directed tangentially to the trajectory.
Consequently
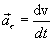 | (1.16) |
Normal acceleration 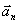 characterizes the rate of change of speed in the direction. Calculate the vector:
characterizes the rate of change of speed in the direction. Calculate the vector:
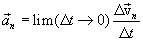
For this we draw a perpendicular through the points M and M1 to the tangents to the trajectory (fig. 1.4) the intersection point we denote by O. For a sufficiently small 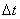 The curved path section can be considered a part of a circle of radius R. The triangles MOM1 and MBC are similar, because they are isosceles triangles with the same angles at the vertices. Therefore:
The curved path section can be considered a part of a circle of radius R. The triangles MOM1 and MBC are similar, because they are isosceles triangles with the same angles at the vertices. Therefore:
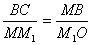
or
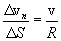
But 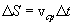 , then:
, then:
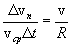
Going to the limit at 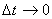 and given that
and given that 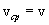 , we find:
, we find:
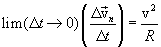 ,
,
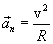 | (1.17) |
Since when 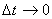 angle
angle 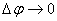 , the direction of this acceleration coincides with the direction of the normal to speed
, the direction of this acceleration coincides with the direction of the normal to speed 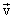 i.e. acceleration vector
i.e. acceleration vector 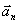 perpendicular
perpendicular 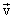 . Therefore, this acceleration is often called centripetal.
. Therefore, this acceleration is often called centripetal.
Full acceleration is determined by the vector sum of the tangential normal accelerations (1.15). Since the vectors of these accelerations are mutually perpendicular, the total acceleration modulus is equal to:
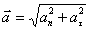 | (1.18) |
The direction of the full acceleration is determined by the angle between the vectors 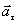 and
and 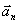 :
:
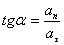
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics