Lecture
Each point of the potential field corresponds, on the one hand, to a certain value of the force vector 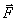 acting on the body and, on the other hand, some value of potential energy
acting on the body and, on the other hand, some value of potential energy 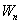 . Consequently, there must be a definite connection between force and potential energy.
. Consequently, there must be a definite connection between force and potential energy.
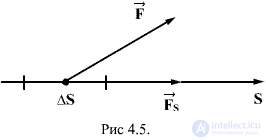
To establish this connection, we calculate the elementary work  performed by field forces with small displacement
performed by field forces with small displacement 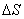 body occurring along an arbitrarily chosen direction in space, which we denote by
body occurring along an arbitrarily chosen direction in space, which we denote by 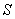 . This job is equal to
. This job is equal to
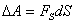
Where 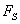 - projection of force
- projection of force 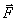 on direction
on direction 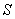 .
.
Since in this case the work is done at the expense of the stock of potential energy 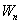 , it is equal to the loss of potential energy
, it is equal to the loss of potential energy 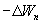 on the axis segment
on the axis segment 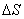 :
:
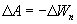
From the last two expressions we get
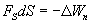
From where
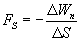
The last expression gives the average 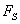 on the segment
on the segment 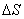 . To
. To
get value 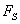 at the point you need to make the limit:
at the point you need to make the limit:
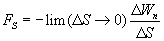
Because 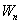 may change not only when moving along the axis
may change not only when moving along the axis 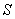 but also when moving along other directions, the limit in this formula represents with robots the so-called partial derivative of
but also when moving along other directions, the limit in this formula represents with robots the so-called partial derivative of 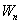 by
by 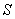 :
:
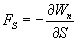
This relation is valid for any direction in space, in particular, for the directions of Cartesian coordinate axes x, y, z:
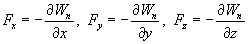
This formula defines the projections of the force vector on the coordinate axes. If these projections are known, the force vector itself is determined:
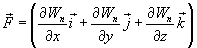
in math vector 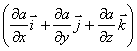 ,
,
where a is the scalar function x, y, z, is called the gradient of this scalar denoted by 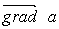 . Hence the force is equal to the gradient of potential energy taken with the opposite sign.
. Hence the force is equal to the gradient of potential energy taken with the opposite sign.
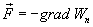 | (4.15) |
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics