Lecture
To find the moment of inertia of the body, it is necessary to sum the moment of inertia of all material points that make up the body.
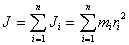 | (5.4) |
In general, if the body is solid, it is a collection of points with infinitely small masses. 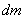 , and the moments of inertia of the body is determined by the integral
, and the moments of inertia of the body is determined by the integral
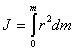 | (5.5) |
about where  - distance from the element
- distance from the element 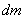 to the axis of rotation.
to the axis of rotation.
The distribution of mass within the body can be characterized by
density
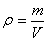 | (5.5) |
where m is the mass of a homogeneous body, V is its volume. For a body with an unevenly distributed mass, this expression gives an average density.
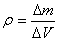
The density at this point in this case is determined as follows.
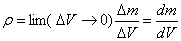
and then
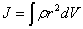 | (5.6) |
The limits of integration depend on the shape and size of the body. Integration of equation (5.5) is most easily implemented for those cases when the axis of rotation passes through the center of gravity of the body. Let us consider the results of integration for the simplest (geometrically regular) forms of a solid body whose mass is uniformly distributed over the volume.
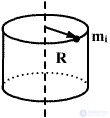
The moment of inertia of a hollow cylinder with thin walls, radius R.
For thin-wall hollow cylinder
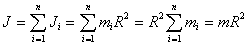
Solid homogeneous disk. The axis of rotation is the axis of the disk radius 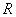 . and mass m with density
. and mass m with density 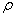 Disk height h. Cut a hollow cylinder with a wall thickness inside the disk at a distance
Disk height h. Cut a hollow cylinder with a wall thickness inside the disk at a distance 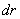 and mass
and mass 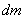 . For him
. For him
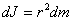
The entire disk can be divided into an infinite number of cylinders, and then summed:
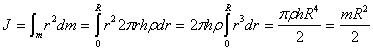
The moment of inertia of the ball relative to the axis passing through the center of gravity.
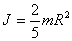
The moment of inertia of a rod of length L and mass m relative to the axis passing:
a) through the center of the rod - 
b) through the beginning of the rod - 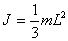
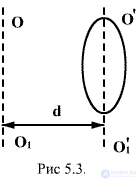
Steiner theorem. We have a body, the moment of inertia of which is relative to the axis passing through its center of mass 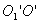 known. It is necessary to determine the moment of inertia about an arbitrary axis.
known. It is necessary to determine the moment of inertia about an arbitrary axis. 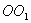 parallel to the axis
parallel to the axis  . According to Steiner’s theorem, the moment of inertia of a body about an arbitrary axis is equal to the sum of the moment of inertia of a body about an axis passing through the center of mass and parallel to this axis, plus the product of the body mass per square of the distance between the axes:
. According to Steiner’s theorem, the moment of inertia of a body about an arbitrary axis is equal to the sum of the moment of inertia of a body about an axis passing through the center of mass and parallel to this axis, plus the product of the body mass per square of the distance between the axes:
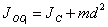 | (5.7) |
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics