2.5. The relationship of angular and linear quantities

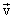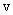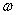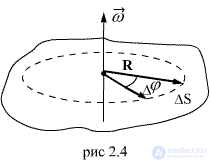
Separate points of a rotating body have different linear velocities. . The speed of each point, being tangential to the corresponding circle, continuously changes its direction. Speed ​​magnitude determined by the speed of body rotation and the distance R of the considered point from the axis of rotation. Let for a small period of time 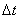the body turned to the corner 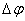(figure 2.4). A point located at a distance R from the axis passes the path equal to

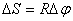
Linear velocity of a point by definition.

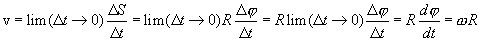(2.6)

Find the linear acceleration points of the rotating body. Normal acceleration:

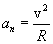
substituting the value of speed from (2.6), we find:

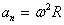(2.7)

Tangential acceleration

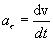
Using the same relation (2.6) we get

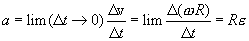(2.8)

Thus, both normal and tangential accelerations grow linearly with the distance of the point from the axis of rotation.