Lecture
The trajectory of a material point is a line described by space as this point as it moves. Depending on the shape of the trajectory, rectilinear and curvilinear motion of a point is distinguished. If all parts of the point trajectory lie in the same plane, then the motion of the point is called flat.
Equations (1.2) and (1.3) define the trajectory of a point in the so-called parametric form. The role of the parameter is time t. Solving these equations together and excluding time t from them, we find the equation of the trajectory.
Path length Long way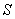 
material point is called the sum of the lengths of all parts of the trajectory, traversed by a point in the considered period of time.
The trajectory (from the late Latin trajectories - referring to displacement) is the line along which the body moves (the material point). The trajectory of movement can be straight (the body moves in one direction) and curvilinear, that is, the mechanical movement can be straight and curvilinear.
The trajectory of the rectilinear motion in this coordinate system is a straight line. For example, we can assume that the trajectory of a car on a flat road without turns is straightforward.
Curvilinear motion is the movement of bodies in a circle, ellipse, parabola or hyperbola. An example of a curvilinear motion is the movement of a point on the wheel of a moving car or the movement of a car in a turn.
Movement can be difficult. For example, the trajectory of the body at the beginning of the path may be rectilinear, then curvilinear. For example, at the beginning of a car, a car moves along a straight road, and then the road starts to “wind” and the car starts a curvilinear motion.
The path is the length of the trajectory. The path is a scalar value and in the international system of units of SI is measured in meters (m). The calculation of the path is performed in many problems in physics. Some examples will be discussed later in this tutorial.
The displacement vector (or simply displacement ) is a directed segment of a straight line connecting the initial position of the body with its subsequent position (Fig. 1.1). The displacement is a vector quantity. The displacement vector is directed from the starting point of the movement to the final one.
The module of the displacement vector (that is, the length of the segment that connects the starting and ending points of the movement) may be equal to the distance traveled or less than the distance traveled. But never the module of the displacement vector can be greater than the distance traveled.
The module of the displacement vector is equal to the distance traveled when the path coincides with the path (see sections Trajectory and Path), for example, if the car moves from point A to point B along a straight road. The module of the displacement vector is less than the distance traveled when the material point moves along a curved path (Fig. 1.1).
In fig. 1.1:
Another example. If the car passes in a circle once, it turns out that the starting point of the movement will coincide with the point of the end of the movement and then the displacement vector will be zero, and the distance traveled will be equal to the circumference. Thus, path and movement are two different things.
Displacement vectors are formed geometrically according to the rule of addition of vectors (a triangle rule or a parallelogram rule, see Fig. 1.2).
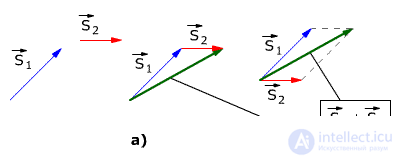
Figure 1.2 shows the addition rules for the vectors S1 and S2:
a) Addition by the rule of a triangle
b) Addition by parallelogram rule
When solving problems in physics, projections of the displacement vector onto coordinate axes are often used. The projections of the displacement vector on the coordinate axes can be expressed in terms of the differences in the coordinates of its end and beginning. For example, if the material point moved from point A to point B, then the displacement vector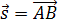 
(Fig. 1.3).
We choose the axis OX so that the vector 
lay with this axis in the same plane. Let us drop the perpendiculars from points A and B (from the initial and final points of the displacement vector) to the intersection with the OX axis. Thus, we obtain the projections of the points A and B on the X axis. We denote the projections of the points A and B, respectively, A x and B x . The length of the segment A x B x on the OX axis is the projection of the displacement vector on the OX axis, i.e.
S
x
= A
x
B
x
with the projection of the vector on any axis (for example, S x ). A vector is always denoted by a letter or several letters above which an arrow is located. In some electronic documents, the arrow is not set, as this may cause difficulties in creating an electronic document. In such cases, be guided by the content of the article, where the word “vector” can be written next to the letter or in some other way they indicate to you that this is exactly a vector, and not just a segment.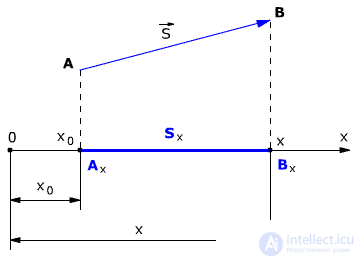 
The projection of the displacement vector on the OX axis is equal to the difference of the coordinates of the end and the beginning of the vector, i.e.
S
x
= x - x
0 Projections of the displacement vector on the OY and OZ axes are determined and recorded in a similar way:
S
y
= y - y
0
S
z
= z - z
0
Here x 0 , y 0 , z 0 - the initial coordinates, or the coordinates of the initial position of the body (material point); x, y, z - final coordinates, or coordinates of the subsequent position of the body (material point).
The projection of the displacement vector is considered positive if the direction of the vector and the direction of the coordinate axis coincide (as in Figure 1.3). If the direction of the vector and the direction of the coordinate axis do not coincide (are opposite), then the projection of the vector is negative (Fig. 1.4).
If the displacement vector is parallel to the axis, then the module of its projection is equal to the module of the Vector itself. If the displacement vector is perpendicular to the axis, then the module of its projection is zero (Fig. 1.4).
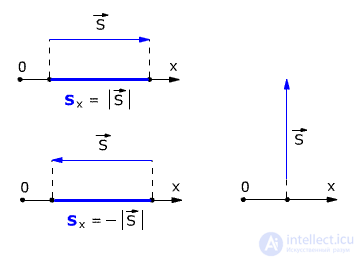
The difference between the subsequent and initial values of some quantity is called the change of this quantity. That is, the projection of the displacement vector onto the coordinate axis is equal to the change in the corresponding coordinate. For example, for the case when the body moves perpendicular to the X axis (Fig. 1.4), it turns out that the body DOES NOT MOVE relative to the X axis. That is, the movement of the body along the X axis is zero.
Consider the example of a body motion on a plane. The initial position of the body is point A with coordinates x 0 and y 0 , that is, A (x 0 , y 0 ). The final position of the body is point B with coordinates x and y, that is, B (x, y). Find the body displacement module.
From points A and B, we lower perpendiculars on the coordinate axes OX and OY (Fig. 1.5).
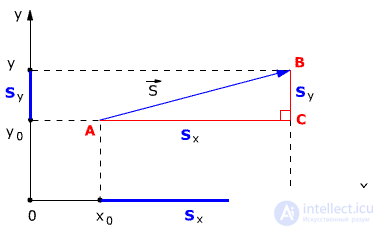
Define the projection of the displacement vector on the axes OX and OY:
S
x
= x - x
0
S
y
= y - y
0
In fig. 1.5 it is clear that the ABC triangle is rectangular. From this it follows that the solution of the problem can be used the Pythagorean theorem , with which you can find the module of the displacement vector, since
AC = s
x
CB = s
y
According to the Pythagorean theorem
S
2
= S
x 2
+ S
y 2
From where you can find the module of the displacement vector, that is, the length of the path of the body from point A to point B:
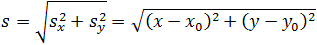
And finally, I suggest you consolidate your knowledge and calculate a few examples at your discretion. To do this, enter any numbers in the coordinate fields and click CALCULATE. Your browser must support the execution of JavaScript scripts (scripts) and the execution of scripts must be enabled in your browser settings, otherwise the calculation will not be performed. In real numbers, the integer and fractional parts must be separated by a period, for example, 10.5.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics