3.2. Concept of power

From the point of view of our personal observations, with which do we associate the “cause of movement”? You can answer with muscular or push. To move the table, we have to push it very hard, whereas only a small amount of effort is needed to move a sheet of paper across the desk. We call these pulling and pushing forces. Thus, by force we understand the physical quantity, which is a measure of the mechanical impact on the body by other bodies.

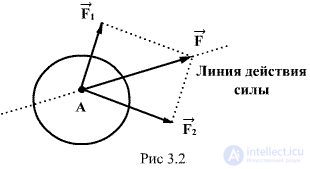
The force applied to the body is fully defined if its numerical value, direction of action and point are indicated; M applications (Fig.3.1). A straight line drawn through the point of application of force in the direction of the action of force is called the line of action of force. Two forces are called numerically equal and opposite in direction if the simultaneous application of these forces at the same point of the body does not cause a change in its mechanical movement. In particular, if before the application of such two forces the body is at rest, then it continues to remain at rest after their application. Therefore, it is said that two numerically equal and oppositely directed forces applied at the same point of the body are mutually balanced. If the body is simultaneously affected by n forces applied at one point A of the body, then they can be replaced by one equivalent force. 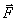equal to their geometric sum

(3.1)

and attached at the same point. That power 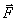called the resultant or resultant force. The effect of a force on an absolutely rigid body does not change when the point of its application is transferred along the line of action.