Lecture
Consider a rod located along the x axis and resting relative to the system K '. Its length in this system is equal to: 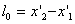 where
where 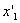 and
and 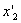 - not changing over time
- not changing over time 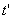 coordinates of the ends of the rod. Regarding the system K, the rod moves with velocity v. To determine its length in this system, it is necessary to note the coordinates of the ends of the rod.
coordinates of the ends of the rod. Regarding the system K, the rod moves with velocity v. To determine its length in this system, it is necessary to note the coordinates of the ends of the rod. 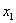 and
and 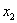 at the same time
at the same time 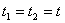 . Their difference
. Their difference 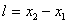 will give the length of the rod, measured in the system K. To find the ratio between
will give the length of the rod, measured in the system K. To find the ratio between 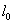 and
and 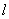 , one should take that of the Lorentz transformation formulas, which contains
, one should take that of the Lorentz transformation formulas, which contains 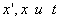 i.e.
i.e.
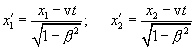
from where
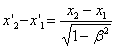
or finally
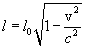
Thus, the length of the rod 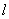 measured in the system with respect to which it moves, is less than the length
measured in the system with respect to which it moves, is less than the length 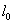 measured in the system relative to which it rests. This phenomenon is called Lorentz contraction.
measured in the system relative to which it rests. This phenomenon is called Lorentz contraction.
The speeds at which the reduction of the size of moving material
bodies becomes noticeable, called relativistic velocities, and now they are achieved on a large scale in laboratory practice and in new industrial devices. In nuclear reactors of nuclear power plants, fast neutrons move with speeds for which 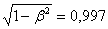 i.e. length reduction of the order of 0.3%. Relativistic particles coming to Earth cosmic rays have
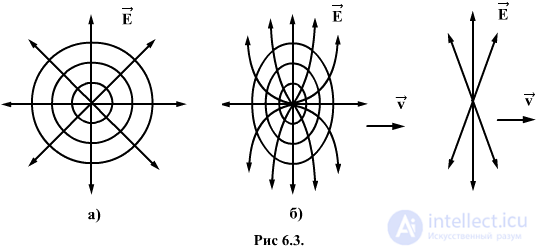
i.e. length reduction of the order of 0.3%. Relativistic particles coming to Earth cosmic rays have 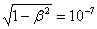 and the longitudinal dimensions are reduced by 10 million times. For rapidly flying charged particles, the accompanying electromagnetic field is subjected to similar longitudinal deformation. Figure 6 shows the field lines and constant potential.
and the longitudinal dimensions are reduced by 10 million times. For rapidly flying charged particles, the accompanying electromagnetic field is subjected to similar longitudinal deformation. Figure 6 shows the field lines and constant potential.  electric field of a point charge when it is stationary. In fig. 6.36 the same charge moving at a not too high speed, in Fig. 6c - at a speed very close to the speed of light. If in the first case the field is spherically symmetric, then in the latter it is practically compressed into a “cake”, perpendicular to the direction of movement. This deformation of the electromagnetic field can be detected by experience. Relativistic particle will interact with a fixed test charge
electric field of a point charge when it is stationary. In fig. 6.36 the same charge moving at a not too high speed, in Fig. 6c - at a speed very close to the speed of light. If in the first case the field is spherically symmetric, then in the latter it is practically compressed into a “cake”, perpendicular to the direction of movement. This deformation of the electromagnetic field can be detected by experience. Relativistic particle will interact with a fixed test charge 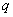 placed in her way only for a very short time when the “tortilla” of the lines of force passes through the charge
placed in her way only for a very short time when the “tortilla” of the lines of force passes through the charge 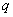 .
.
It is curious that visually (or in a photograph) changing the shape of the body, even at speeds comparable with the speed of light, cannot be detected. The reason for this is quite simple. Observing visually or photographing any body, we register light impulses from different parts of the body that reach simultaneously the retina of the eye or photographic plate. These pulses are not emitted simultaneously. Impulses from more distant parts of the body were emitted earlier than from closer parts. Thus, if the body moves, a distorted body image is obtained on the retina. The corresponding calculation shows that the consequence of the distortion will be the destruction of the Lorentz contraction, so that the bodies do not seem distorted, but only turned. If there was no Lorentz contraction, the bodies would appear elongated in the direction of motion.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics