Lecture
Based on the Einstein's theory of relativity formulated above, it is possible to find transformation laws connecting the spatial coordinates and time between themselves in two frames of reference, moving in a straight line and uniformly relative to each other.
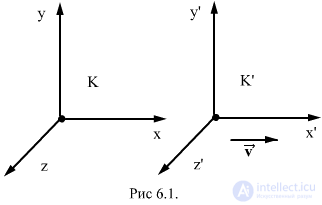
Let x, y, z, and x ', y', z 'and t', be the coordinates and time in the inertial reference systems K and K ', and v be the speed of their relative motion (Fig. 6.1).
However, there is no reason to believe that the time in the system 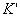 coincides with time in the system K, as it was unconditionally accepted in classical physics. For the expanses of the calculations, we choose the direction of velocity for the direction of the axes x and
coincides with time in the system K, as it was unconditionally accepted in classical physics. For the expanses of the calculations, we choose the direction of velocity for the direction of the axes x and 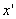 . Suppose that at some point in time t 'at a point by coordinates
. Suppose that at some point in time t 'at a point by coordinates 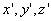 there is some physical process that we call an event. Our task is to find the "coordinates" of the event in the frame of reference K ', i.e. finding the values of x, y, z, t characterizing the same physical process in the system K.
there is some physical process that we call an event. Our task is to find the "coordinates" of the event in the frame of reference K ', i.e. finding the values of x, y, z, t characterizing the same physical process in the system K.
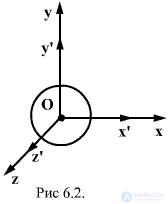
For the origin of time t = 0, we choose the moment at which the origin of system K 'coincided with the origin of system K. Let a spherical electromagnetic wave begin to propagate at time t = 0 from the origin of coordinates (Fig. 6.2). In system K, the wave surface equation has the form.
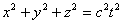
or
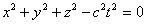 | (6.1) |
Since, according to Einstein's principle of relativity, the law and magnitude of the wave propagation velocity should be the same in all inertial reference frames, along with this equation, with equal rights, we can write the equation of a spherical wave in the system K '.
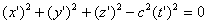
Since at the initial moment of time the origin of the systems coincided,
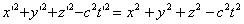 | (6.2) |
The formulas for the transformation of coordinates and time must, firstly, not violate relations (6.1) and (6.2), and, secondly, be linear. The requirements of linearity are related to the homogeneity of space. Because the motion of the system K 'occurs only along the x axis; the transformation of the coordinates y and z should be
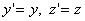
The law of transformation x 'through x can be written on the basis of the following image: if at the time t = 0 the origin of the coordinate systems K and K' coincided, then the coordinate of the plane x 'in the system K is written x = νt. Therefore, in the most general case, you can write
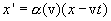 | (6.3) |
where is the coefficient 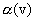 may depend only on the speed of relative motion. Without making any arbitrary assumptions about the coincidence of time in the two reference systems, we can represent t 'as a linear homogeneous function x and t
may depend only on the speed of relative motion. Without making any arbitrary assumptions about the coincidence of time in the two reference systems, we can represent t 'as a linear homogeneous function x and t
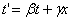 | (6.4) |
Factors 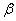 and
and 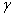 may, generally speaking, depend on the velocity v. If it turned out that
may, generally speaking, depend on the velocity v. If it turned out that 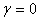 , but
, but 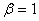 then we would return to the transformations of Galileo. To determine the coefficients
then we would return to the transformations of Galileo. To determine the coefficients 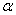 ,
, 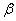 and
and 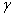 that meet the requirements of the Einstein principle of relativity, we must substitute (6.3) and (6.5) into (6.2). This gives
that meet the requirements of the Einstein principle of relativity, we must substitute (6.3) and (6.5) into (6.2). This gives
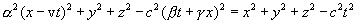
To fulfill the identity, it is necessary to equate the coefficients at x 2 , t 2 and xt. Opening the brackets and performing the appropriate transformations we get:
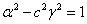
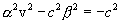
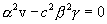
From these three equations we find the unknown values. 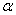 ,
, 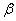 and
and 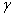 ,:
,:
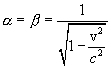


At the same time everywhere we chose the positive sign of the root. Substituting values 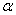 ,
, 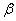 and
and 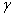 in the coordinate transformations (6.3) and (6.4) we find:
in the coordinate transformations (6.3) and (6.4) we find:
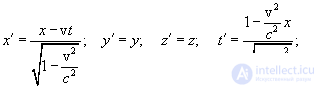 | (6.5) |
These formulas are called Lorentz transformations. Inverse transform formulas from primed to non-primed values:
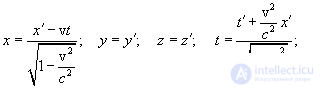 | (6.6) |
The Lorentz transformations lead to conclusions that fundamentally contradict the usual notions about the properties of time and space that have developed on the basis of everyday experience. Consider a few examples of the application of Lorentz transformations.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics